Línea eléctrica entre dos torres. Aplicaciones de cálculo diferencial.

Problema 6. Una línea eléctrica de alta tensión entre dos torres tiene la forma de una catenaria:

$\displaystyle y = 25({e}^{\frac{x}{50}} + {e}^{-\frac{x}{50}})$

Si las torres distan entre sí 100 m, calcular:

a) El ángulo formado por el cable con una de las torres.

b) La dirección del cable en el punto medio entre las dos torres.

c) Dirección del cable cuando dista de una de las torres 20 m.

d) Punto en donde el cable forma con la horizontal un ángulo de 28°.

e) El punto donde el cable va vertical.

Imagen23 — *Figura 1.5.1 Representación gráfica de la catenaria.*

Solución. Derivando la función:

$\displaystyle y = 25({e}^{\frac{x}{50}} + {e}^{-\frac{x}{50}})$

$\displaystyle \frac {dy}{dx} = \frac{d}{dx} \left[25({e}^{\frac{x}{50}} + {e}^{-\frac{x}{50}}) \right] = 25 \frac{d}{dx} ({e}^{\frac{x}{50}} + {e}^{-\frac{x}{50}})$

$\displaystyle \frac{dy}{dx} = 25 \left[\frac{d}{dx} ({e}^{\frac{x}{50}}) + \frac{d}{dx} ({e}^{-\frac{x}{50}}) \right]$

$\displaystyle \frac{dy}{dx} = 25 (\frac{1}{50} {e}^{\frac{x}{50}} - \frac{1}{50} {e}^{-\frac{x}{50}}) = \frac{25}{50} ({e}^{\frac{x}{50}} - {e}^{-\frac{x}{50}})$

$\displaystyle \frac{dy}{dx} = \frac{1}{2} ({e}^{\frac{x}{50}} - {e}^{-\frac{x}{50}})$

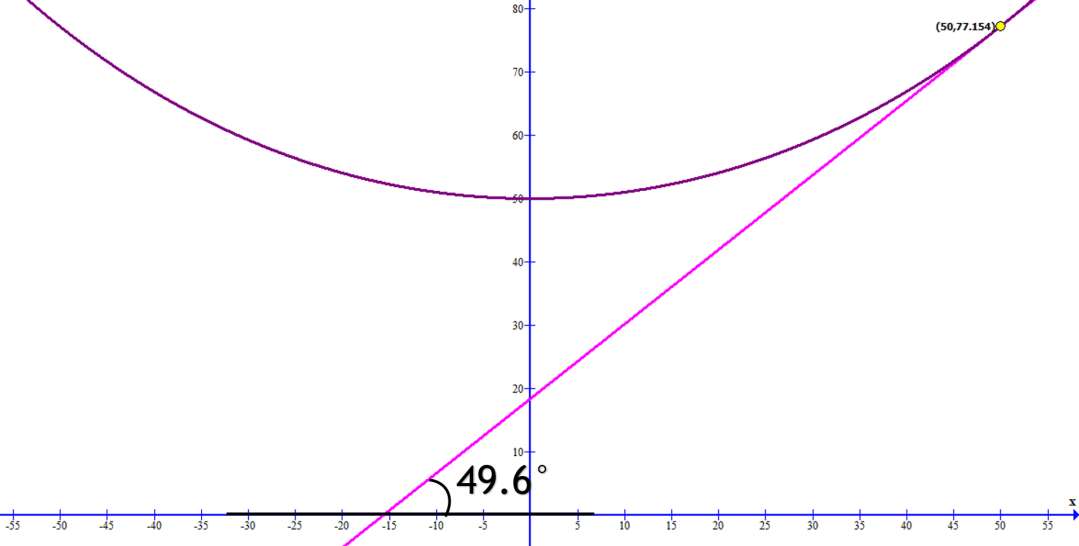
Del a), para obtener el ángulo entre el cable y la torre, se debe tener en cuenta lo siguiente, si x = 50 m:

$\displaystyle y = 25 ({e}^{\frac{x}{50}} + {e}^{-\frac{x}{50}})$

$\displaystyle y = 25 ({e}^{\frac{50}{50}} + {e}^{-\frac{50}{50}}) = 77.154 (m)$

Tomando el punto (50,77.154) y sustituyéndolo en el resultado de la derivada:

$\displaystyle \frac{dy}{dx} = \frac{1}{2} ({e}^{\frac{x}{50}} - {e}^{-\frac{x}{50}})$

$\displaystyle \frac{dy}{dx}{|}_{P(50,77.154)} = \frac{1}{2} ({e}^{\frac{50}{50}} - {e}^{-\frac{50}{50}}) = 1.175$

$\displaystyle {m}_{tan} = \frac{dy}{dx}{|}_{P(50,77.154)} = 1.175$

$\tan{\alpha} = {m}_{tan} = 1.175$

$\alpha = \arctan{(1.175)} = 49.6$ °

“Alpha” es el ángulo que va de la pendiente con respecto a la horizontal, para obtener lo deseado, se aplica la propiedad de los triángulos internos:

Imagen24 — *Figura 1.6.2 Triángulo escaleno.*

$90 + \alpha + \beta = 180$ °

$\beta = 180 - 90 - \alpha$

$\beta = 90 - \alpha = 90 - 49.6 = 40.4$ °

$\therefore \beta = 40.4$ °

Por lo tanto, el ángulo que se forma entre el cable y la torre, es de 40.4°.

Imagen25 — *Figura 1.6.3 Representación gráfica de la dirección de la recta tangente.*

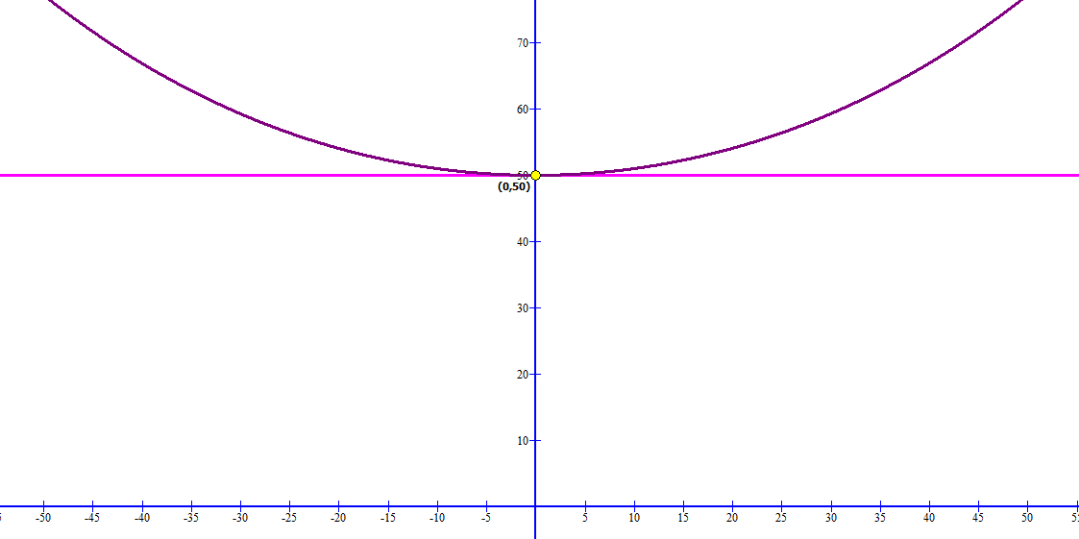
Del b), si se desea obtener la dirección del cable en el punto medio entre las dos torres, solo basta con asignar a “x = 0”. Y así:

$\displaystyle y = 25 ({e}^{\frac{x}{50}} + {e}^{-\frac{x}{50}})$

$\displaystyle y = 25 ({e}^{0} + {e}^{(-0)})$

$y = 50$

Después, usando el punto (0,50):

$\displaystyle \frac{dy}{dx}{|}_{P(0,50)} = \frac{1}{2} ({e}^{(\frac{0}{50})} - {e}^{(-\frac{0}{50})}) = 0$

$\displaystyle {m}_{tan} = \frac{dy}{dx}{|}_{P(0,50)} = 0$

$\tan{\alpha} = {m}_{tan} = 0$

$\alpha = \arctan{(0)} = 0$

Entonces, el cable va en horizontal, es decir, va a 0°.

Imagen26 — *Figura 1.6.4 Representación gráfica cuando el cable esté en el punto medio de las dos torres.*

Del c), si el cable dista desde el origen hasta la torre (se toma en cuenta el de la derecha) 20 m, habrá una altura de:

$\displaystyle y = 25 ({e}^{(\frac{x}{50})} + {e}^{(-\frac{x}{50})})$

$\displaystyle y = 25 ({e}^{(\frac{20}{50})} + {e}^{(-\frac{20}{50})}) = 54.054$

$y = 54.054 (m)$

Tomando este nuevo punto (20, 54.054), la dirección es:

$\displaystyle \frac{dy}{dx}{|}_{P(20,54.054)} = \frac{1}{2} ({e}^{(\frac{20}{50})} - {e}^{(-\frac{20}{50})}) = 0.411$

$\displaystyle {m}_{tan} = 0.411$

$\displaystyle \tan{\alpha} = {m}_{tan} = 0.411$

$\alpha = \arctan{(0.411)} = 22.34$ °

Así que, a 20 metros, el cable forma un ángulo de 22.34° con respecto al eje x (a la horizontal).

Imagen27 — *Figura 1.6.5 Representación gráfica cuando el cable forma una dirección a 20 (m).*

Del d), si el cable forma un ángulo de 28°, el procedimiento es inverso:

${m}_{tan} = \tan{\alpha}$

$\displaystyle {dy}{dx}{|}_{P({x}_{1},{y}_{1})} = \tan{\alpha}$

$\displaystyle \frac{1}{2} ({e}^{(\frac{{x}_{1}}{50})} - {e}^{(-\frac{{x}_{1}}{50})}) = \tan{28}$

$\displaystyle {e}^{(\frac{{x}_{1}}{50})} - {e}^{(-\frac{{x}_{1}}{50})} = 1.063$

$\displaystyle {e}^{(\frac{{x}_{1}}{50})} - \frac{1}{{e}^{(\frac{{x}_{1}}{50})}} = 1.063$

$\displaystyle \frac{{e}^{(\frac{2{x}_{1}}{50})} - 1}{{e}^{(\frac{{x}_{1}}{50})}} = 1.063$

$\displaystyle {e}^{(\frac{2{x}_{1}}{50})} - 1 = 1.063{e}^{(\frac{{x}_{1}}{50})}$

$\displaystyle {e}^{(\frac{2{x}_{1}}{50})} - 1.063{e}^{(\frac{{x}_{1}}{50})} - 1 = 0$

$\displaystyle {({e}^{\frac{{x}_{1}}{50}})}^{2} - 1.063({e}^{\frac{{x}_{1}}{50}}) - 1 = 0$

Sustituyendo $\displaystyle h = {e}^{(\frac{{x}_{1}}{50})}$ :

${h}^{2} - 1.063h - 1 = 0$

Resolviendo por fórmula general:

$\displaystyle h = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-(-1.063) \pm \sqrt{(-1.063)^2 - 4(1)(-1)}}{2(1)}$

$\displaystyle h = \frac{1.063 \pm 2.265}{2}$

${h}_{1} = 1.664 \quad y \quad {h}_{2} = -0.601$

Si se selecciona h_1, por propiedades de los logaritmos, se obtiene del valor de x_1:

${h}_{1} = 1.664$

$\displaystyle {e}^{(\frac{{x}_{1}}{50})} = 1.664$

$\displaystyle \ln{{e}^{\frac{{x}_{1}}{50}}} = \ln{1.664}$

$\frac{{x}_{1}}{50} \ln{e} = \ln{1.664}$

$\displaystyle {x}_{1} = 25.461 (m)$

Si se selecciona h_2, por propiedades de los logaritmos no habría solución. Por lo tanto, si el cable forma un ángulo de 28°, tendrá una distancia (contando desde origen hasta el punto) de 25.461 (m) aproximadamente.

Del e), si el cable llegara a estar en vertical, formaría un ángulo de 90° con respecto a la horizontal. Entonces:

$\displaystyle {m}_{tan} = \frac{dy}{dx}{|}_{P({x}_{2},{y}_{2})} = \tan{\alpha}$

$\displaystyle \frac{1}{2} ({e}^{\frac{{x}_{2}}{50}} - {e}^{-\frac{x_2}{50}} ) = \tan{90}$

$\displaystyle \frac{1}{2} ({e}^{\frac{{x}_{2}}{50}} - {e}^{-\frac{{x}_{2}}{50}} ) = \infty$

$\displaystyle {e}^{\frac{{x}_{2}}{50}} - {e}^{-\frac{{x}_{2}}{50}} = \infty$

$\displaystyle \frac{{e}^{\frac{2{x}_{2}}{50}} - 1}{{e}^{\frac{{x}_{2}}{50}}} = \infty$

En este caso, el cable no alcanzaría en la dirección de 90°.

Línea eléctrica entre dos torres. Aplicaciones de cálculo diferencial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Línea eléctrica entre dos torres. Aplicaciones de cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta