Área en coordenadas polares y área entre dos curvas. Cálculo vectorial.

Introducción

Si f es continua y no negativa en el intervalo $[\alpha, \beta]$ , $0<\beta - \alpha<2\pi$ , entonces el parea de la región limitada (o acotada) por la gráfica de $r = f(\theta)$ entre las rectas radiales $\theta = \alpha$ y $\theta = \beta$ está dada por:

$\displaystyle A = \frac{1}{2} \int _{\alpha}^{\beta}{{[f(\theta)]}^{2} d\theta}$

$\displaystyle A = \frac{1}{2} \int _{\alpha}^{\beta}{r^2 d\theta}$

donde $(0< \beta - \alpha < 2\pi)$

Problemas resueltos

Problema 1. Encontrar el área de una región polar de $r = 3 \cos{3\theta}$ .

Solución. Primero se despeja la variable θ de la función $r$

$r = 3 \cos{3\theta}$

$0 = 3 \cos{3\theta}$

$\displaystyle \frac{0}{3} = \cos{3\theta}$

$0 = \cos{3\theta}$

$\cos{3\theta} = 0$

$3\theta = \arccos{(0)}$

$\displaystyle 3\theta = \pm \frac{1}{2} \pi$

$\displaystyle \theta = \pm \frac{1}{6} \pi = \pm \frac{\pi}{6}$

Por lo que el intervalo es

$\displaystyle - \frac{1}{6} \pi < \theta < \frac{1}{6} \pi$

Así que, en la ecuación $r = 3 \cos{3\theta}$ , dentro del intervalo obtenido, los límites son $\displaystyle \alpha = -\frac{\pi}{6}$ y $\displaystyle \beta = \frac{\pi}{6}$ . Sustituyendo en la ecuación.

$\displaystyle A = \frac{1}{2} \int _{\alpha}^{\beta}{r^2 d\theta}$

$\displaystyle A = \frac{1}{2} \int _{-\frac{\pi}{6}}^{\frac{\pi}{6}}{{\left(3 \cos{3\theta} \right)}^{2} \ d\theta} = \frac{1}{2} \int _{-\frac{\pi}{6}}^{\frac{\pi}{6}}{9 {\cos}^{2}{3\theta} \ d\theta}$

$\displaystyle A = \frac{9}{2} \int_{-\frac{\pi}{6}}^{\frac{\pi}{6}}{{\cos}^{2}{3\theta} \ d\theta} = \frac{9}{2} \int _{-\frac{\pi}{6}}^{\frac{\pi}{6}}{(\frac{1}{2} + \frac{1}{2} \cos{6\theta}) \ d\theta}$

$\displaystyle A = \frac{9}{2} {\left[\frac{1}{2} \theta + \frac{1}{12} \sin{6\theta} \right]}_{-\frac{\pi}{6}}^{\frac{\pi}{6}} = \frac{9}{2} \left[\left(\frac{\pi}{12} + \frac{1}{12} \sin{\frac{6\pi}{6}} \right) - \left(-\frac{\pi}{12} - \frac{1}{12} \sin{\frac{6\pi}{6}} \right) \right]$

$\displaystyle A = \frac{9}{2} \left[ \left(\frac{\pi}{12} + \frac{1}{12} \sin{\pi} \right) + \left(\frac{\pi}{12} + \frac{1}{12} \sin{\pi} \right) \right]$

$\displaystyle A = \frac{9}{2} \left(\frac{2 \pi}{12} + \frac{2}{12} \sin{\pi} \right) = \left(\frac{18 \pi}{24} + \frac{18}{24} \sin{\pi} \right) = \frac{18}{24} \pi = \frac{3}{4} \pi$

Por lo tanto, el área es

$\displaystyle \therefore A = \frac{3}{4} \pi \ \text{u}^2$

Imagen1 — *Figura 1. Representación gráfica del área de la región para la ecuación r=3 cos 3θ*

Problema 2. Hallar el área limitada por una sola curva: región comprendida entre los lazos interior y exterior de un caracol, $r = 1 - 2 \sin{\theta}$

Solución. Para el lazo interior, se inicia con igualar a cero la ecuación $r = 1 - 2 \sin{\theta}$ .

$r = 1 - 2 \sin{\theta}$

$0 = 1 - 2 \sin{\theta}$

$2 \sin{\theta} = 1$

$\displaystyle \sin{\theta} = \frac{1}{2}$

$\displaystyle \theta = \arcsin{(\frac{1}{2})}$

Donde los valores de θ son $\displaystyle \theta = \frac{\pi}{6}$ y $\displaystyle \theta= \pi - \frac{\pi}{6} = \frac{5}{6} \pi$ .

Imagen2 — *Figura 2. Analizando los límites para el lazo interior (LI) por medio de la gráfica en base a la ecuación r = 1 – 2 sen θ.*

Tomando los valores de los ángulos obtenidos anteriormente, el límite inferior es $\displaystyle \alpha = \frac{\pi}{6}$ y el límite superior es $\displaystyle \beta = \frac{5\pi}{6}$ .

$\displaystyle {A}_{LI} = \frac{1}{2} \int _{\alpha}^{\beta}{r^2 \ d\theta}$

$\displaystyle {A}_{LI} = \frac{1}{2} \int _{\frac{\pi}{6}}^{\frac{5\pi}{6}}{{(1 - 2\sin{\theta})}^{2} d\theta} = \frac{1}{2} \int _{\frac{\pi}{6}}^{\frac{5\pi}{6}}{(1 - 4\sin{\theta} + 4{\sin}^{2}{\theta}) \ d\theta}$

Recordando que, la identidad trigonométrica $\displaystyle {\sin}^{2}{\theta} = \frac{1}{2} - \frac{1}{2} {\cos}^{2}{\theta}$ , entonces

$\displaystyle {A}_{LI} = \frac{1}{2} \int _{\frac{\pi}{6}}^{\frac{5\pi}{6}}{(1 - 4\sin{\theta} + 4{\sin}^{2}{\theta}) \ d\theta}$

$\displaystyle {A}_{LI} = \frac{1}{2} \int _{\frac{\pi}{6}}^{\frac{5\pi}{6}}{\left[1 - 4\sin{\theta} + 4 \left(\frac{1}{2} - \frac{1}{2}\cos{2\theta} \right) \right] \ d\theta}$

$\displaystyle {A}_{LI} = \frac{1}{2} \int _{\frac{\pi}{6}}^{\frac{5\pi}{6}}{ \left(1 - 4\sin{\theta} + 2 - 2\cos{2\theta} \right) \ d\theta}$

$\displaystyle {A}_{LI} = \frac{1}{2} \int _{\frac{\pi}{6}}^{\frac{5\pi}{6}}{\left(3 - 4\sin{\theta} - 2\cos{2\theta} \right)} \ d\theta$

$\displaystyle {A}_{LI} = \frac{1}{2} \left[3\theta + 4\cos{\theta} - \sin{2\theta} \right]_{\frac{\pi}{6}}^{\frac{5\pi}{6}}$

$\displaystyle {A}_{LI} = \frac{1}{2} \left\{ \left[3 \left( \frac{5\pi}{6} \right) + 4 \cos{\frac{5\pi}{6}} - \sin{2 \left(\frac{5\pi}{6} \right)} \right] - \left[3 \left( \frac{\pi}{6} \right) + 4 \cos{\frac{\pi}{6}} - \sin{2 \left(\frac{\pi}{6} \right)} \right] \right\}$

$\displaystyle {A}_{LI} = \frac{1}{2} \left[ \left(\frac{15\pi}{6} + 4 \cos{\frac{5\pi}{6}} - \sin{\frac{5\pi}{3}} \right) - \left(\frac{3\pi}{6} + 4 \cos{\frac{\pi}{6}} - \sin{\frac{\pi}{3}} \right) \right]$

$\displaystyle {A}_{LI} = \frac{1}{2} \left(\frac{15\pi}{6} - \frac{4\sqrt{3}}{2} + \frac{\sqrt{3}}{2} - \frac{3\pi}{6} - \frac{4\sqrt{3}}{2} + \frac{\sqrt{3}}{2} \right)$

$\displaystyle {A}_{LI} = \frac{1}{2} \left(\frac{12\pi}{6} - \frac{8\sqrt{3}}{2} + \frac{2\sqrt{3}}{2} \right)$

$\displaystyle {A}_{LI} = \frac{1}{2} \left(\frac{12\pi}{6} - \frac{6\sqrt{3}}{2} \right) = \frac{1}{2} \left(2\pi - 3\sqrt{3} \right)$

Por lo tanto, el área para el lazo interior es

$\displaystyle {A}_{LI} = \frac{1}{2} (2\pi - 3\sqrt{3}) \ \text{u}^2$

Para el lazo exterior, se toman en cuenta los siguientes límites:

$\displaystyle \theta = \pi - \frac{1}{6} \pi = \frac{5}{6} \pi$ y $\displaystyle \theta = \pi + \frac{5}{6} \pi = \frac{13}{6} \pi$

donde el límite inferior es $\displaystyle \alpha = \frac{5}{6}\pi = \frac{5\pi}{6}$ y el límite superior es $\displaystyle \beta = \frac{13}{6}\pi = \frac{13\pi}{6}$ .

Imagen3 — *Figura 3. Analizando los límites para el lazo exterior (LE) por medio de la gráfica en base a la ecuación r = 1 – 2 sen θ.*

Ahora

$\displaystyle {A}_{LE} = \frac{1}{2} \int _{\alpha}^{\beta}{r^2 d\theta}$

$\displaystyle {A}_{LE} = \frac{1}{2} \int _{\frac{5\pi}{6}}^{\frac{13\pi}{6}}{{(1 - 2\sin{\theta})}^{2} d\theta}$

$\displaystyle {A}_{LE} = \frac{1}{2} \int _{\frac{5\pi}{6}}^{\frac{13\pi}{6}}{(1 - 4\sin{\theta} + 4{\sin}^{2}{\theta}) d\theta}$

$\displaystyle {A}_{LE} = \frac{1}{2} \int _{\frac{5\pi}{6}}^{\frac{13\pi}{6}}{[1 - 4\sin{\theta} + 4(\frac{1}{2} - \frac{1}{2} \cos{2\theta})] d\theta}$

$\displaystyle {A}_{LE} = \frac{1}{2} \int _{\frac{5\pi}{6}}^{\frac{13\pi}{6}}{(1 - 4\sin{\theta} + \frac{4}{2} - \frac{4}{2} \cos{2\theta}) d\theta}$

$\displaystyle {A}_{LE} = \frac{1}{2} \int _{\frac{5\pi}{6}}^{\frac{13\pi}{6}}{(1 - 4\sin{\theta} + 2 - 2\cos{2\theta}) d\theta}$

$\displaystyle {A}_{LE} = \frac{1}{2} \int _{\frac{5\pi}{6}}^{\frac{13\pi}{6}}{(3 - 4\sin{\theta} - 2\cos{2\theta}) d\theta}$

$\displaystyle {A}_{LE} = \frac{1}{2} \left[3\theta + 4\cos{\theta} - \sin{2\theta}\right]_{\frac{5\pi}{6}}^{\frac{13\pi}{6}}$

$\displaystyle {A}_{LE} = \frac{1}{2} \left\{ \left[(3) \left(\frac{13\pi}{6} \right) + 4\cos{\frac{13\pi}{6}} - \sin{2 \left(\frac{13\pi}{6} \right)} \right] - \left[ (3) \left(\frac{5\pi}{6} \right) + 4\cos{\frac{5\pi}{6}} - \sin{2 \left(\frac{5\pi}{6} \right)} \right] \right\}$

$\displaystyle {A}_{LE} = \frac{1}{2} \left\{ \left[\frac{39\pi}{6} + 4 \left(\frac{\sqrt{3}}{2} \right) - \frac{\sqrt{3}}{2} \right] - \left[\frac{15\pi}{6} - 4 \left(\frac{\sqrt{3}}{2} \right) - \left(-\frac{\sqrt{3}}{2} \right) \right] \right\}$

$\displaystyle {A}_{LE} = \frac{1}{2} \left(\frac{39\pi}{6} + \frac{4\sqrt{3}}{2} - \frac{\sqrt{3}}{2} - \frac{15\pi}{6} + \frac{4\sqrt{3}}{2} - \frac{\sqrt{3}}{2} \right)$

$\displaystyle {A}_{LE} = \frac{1}{2} \left(\frac{24\pi}{6} + \frac{6\sqrt{3}}{2} \right) = \frac{1}{2} (4\pi + 3\sqrt{3})$

Por lo que, el área exterior es

$\displaystyle {A}_{LE} = \frac{1}{2} (4\pi + 3\sqrt{3}) \ \text{u}^2$

Para obtener el área total, se lleva a cabo una diferencia de áreas, entre el área del lazo exterior y el área del lazo interior.

$A = {A}_{LE} - {A}_{LI}$

$\displaystyle A = \frac{1}{2} (4\pi + 3\sqrt{3}) - \frac{1}{2} (2\pi - 3\sqrt{3})$

$\displaystyle A = \frac{1}{2} [(4\pi + 3\sqrt{3}) - (2\pi - 3\sqrt{3})]$

$\displaystyle A = \frac{1}{2} (4\pi + 3\sqrt{3} - 2\pi + 3\sqrt{3})$

$\displaystyle A = \frac{1}{2} (2\pi + 6\sqrt{3}) = 3\pi + 3\sqrt{3}$

Por lo tanto, el área calculada es

$\displaystyle \therefore A = 3\pi + 3\sqrt{3} \ \text{u}^2 \approx 8.3378 \ \text{u}^2$

Problemas resueltos. Área entre dos curvas.

Problema 3. Hallar el área de la región entre dos curvas: $r = -6 \cos{\theta}$ y $r = 2 - 2\cos{\theta}$ .

Solución.

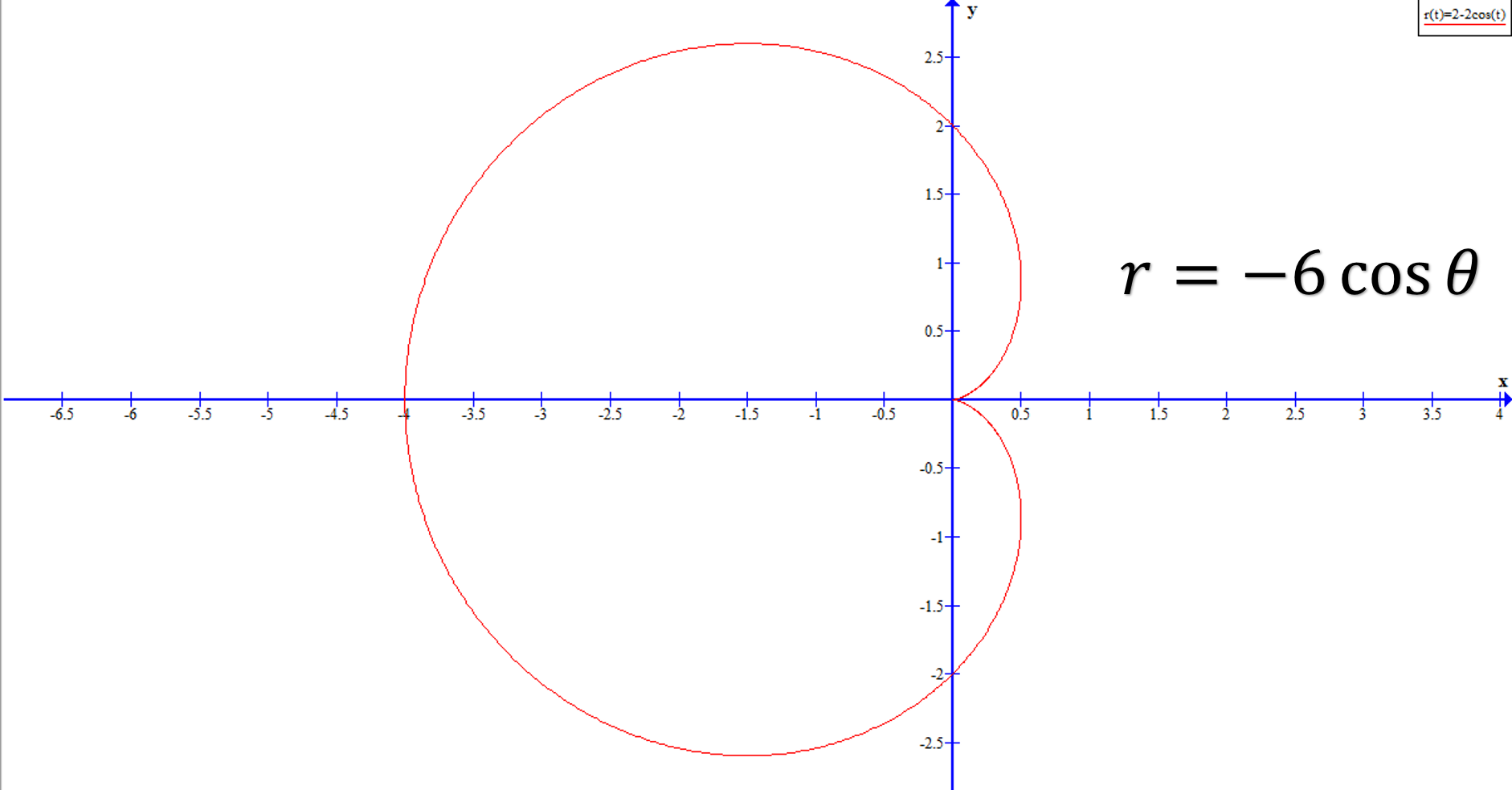
Imagen4 — *Figura 4. Representación gráfica de la ecuación $r = -6 \cos{\theta}$ .*

*Figura 4. Representación gráfica de la ecuación $r = -6 \cos{\theta}$ .*

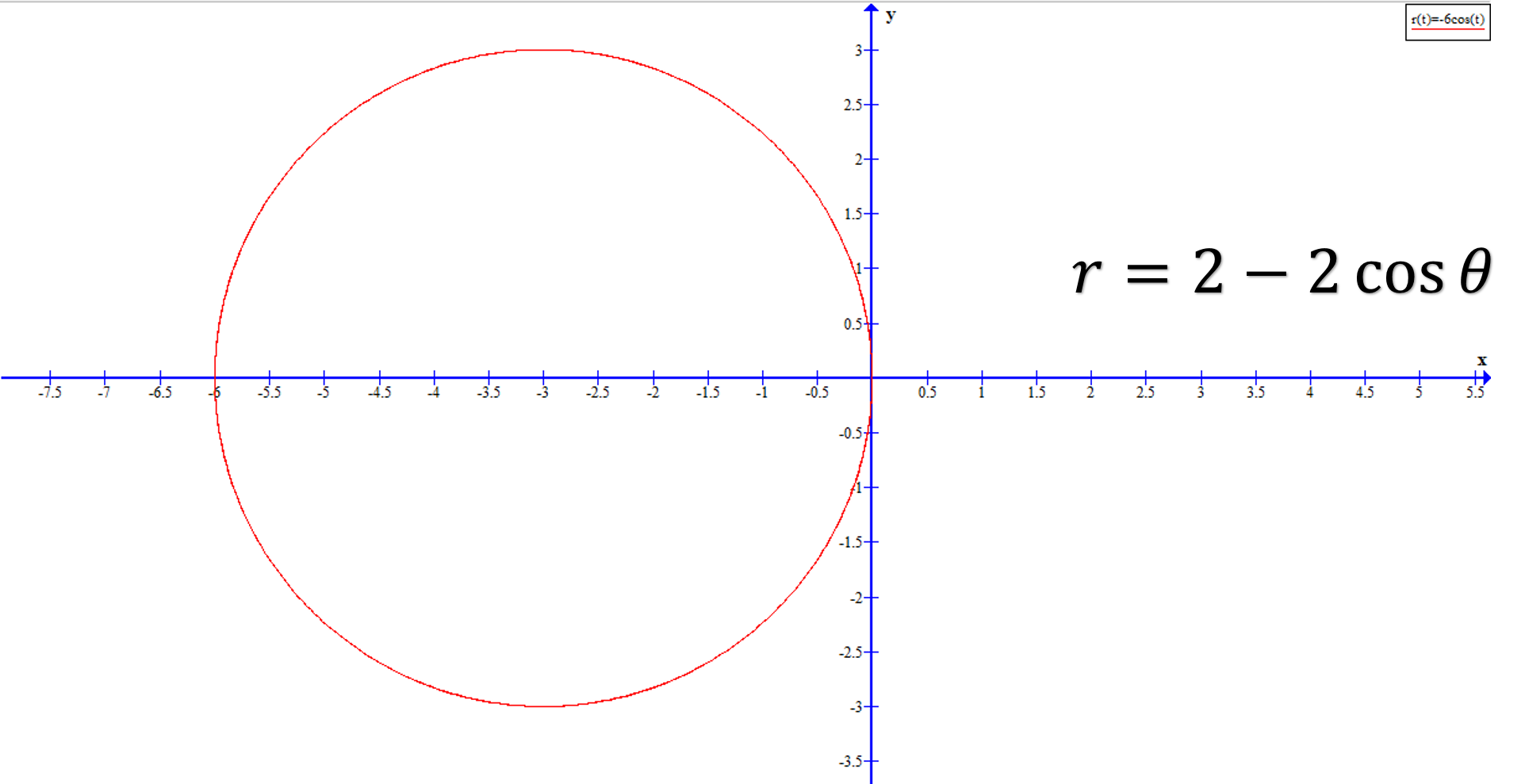
Imagen5 — *Figura 5. Representación gráfica de la ecuación $r = 2 - 2\cos{\theta}$ .*

*Figura 5. Representación gráfica de la ecuación $r = 2 - 2\cos{\theta}$ .*

Imagen6 — *Figura 6. Representación gráfica de las ecuaciones $r = - 6\cos{\theta}$ y $r = 2 - 2\cos{\theta}$ .*

Utilizando la primera ecuación e igualándola con la segunda ecuación, se puede obtener los límites inferior y superior.

$r = -6\cos{\theta}$

$2 - 2\cos{\theta} = -6\cos{\theta}$

$2 - 2\cos{\theta} + 6\cos{\theta} = 0$

$2 + 4\cos{\theta} = 0$

$\displaystyle \cos{\theta} = -\frac{1}{2}$

$\displaystyle \theta = \arccos{(-\frac{1}{2})} = \frac{2}{3} = \frac{2\pi}{3}$

Imagen7 — *Figura 7. Analizando los límites en base a las ecuaciones $r = - 6\cos{\theta}$ y $r = 2 - 2\cos{\theta}$ .*

Imagen8 — *Figura 8. Representación de la primera región.*

Imagen9 — *Figura 9. Representación de la segunda región.*

Ahora

$\displaystyle A = \frac{1}{2} \int _{\alpha}^{\beta}{r^2 d\theta} = \frac{1}{2} \left[2\int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{{(-6 \cos{\theta})}^{2} d\theta} + 2\int _{\frac{2\pi}{3}}^{\pi}{{(2 - 2 \cos{\theta})}^{2} d\theta}\right]$

$\displaystyle A = \frac{1}{2} (2) \int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{{(-6 \cos{\theta})}^{2} d\theta} + \frac{1}{2} (2) \int _{\frac{2\pi}{3}}^{\pi}{{(2 - 2 \cos{\theta})}^{2} d\theta}$

$\displaystyle A = \int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{{(-6 \cos{\theta})}^{2} d\theta} + \int _{\frac{2\pi}{3}}^{\pi}{{(2 - 2 \cos{\theta})}^{2} d\theta}$

$\displaystyle A = \int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{36 {\cos}^{2}{\theta} d\theta + \int _{\frac{2\pi}{3}}^{\pi}{(4 - 8 \cos{\theta} + 4 {\cos}^{2}{\theta})} d\theta}$

$\displaystyle A = 36\int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{{cos}^{2}{\theta} d\theta} + 4\int _{\frac{2\pi}{3}}^{\pi} d\theta - 8\int _{\frac{2\pi}{3}}^{\pi}{\cos{\theta} d\theta} + 4\int _{\frac{2\pi}{3}}^{\pi}{{cos}^{2}{\theta} d\theta}$

Recordando la siguiente identidad trigonométrica ${\cos}^{2}{\theta} = \frac{1}{2} + \frac{1}{2} \cos{2\theta}$ , entonces, sustituyendo la primera y última integral por la ecuación equivalente

$\displaystyle A = 36\int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{{\cos}^{2}{\theta} d\theta} + 4\int _{\frac{2\pi}{3}}^{\pi}{d\theta} - 8\int _{\frac{2\pi}{3}}^{\pi}{cos{\theta} d\theta} + 4\int _{\frac{2\pi}{3}}^{\pi}{{\cos}^{2}{\theta} d\theta}$

$\displaystyle A = 36\int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{(\frac{1}{2} + \frac{1}{2} \cos{2\theta}) d\theta} + 4\int _{\frac{2\pi}{3}}^{\pi}{d\theta} - 8\int _{\frac{2\pi}{3}}^{\pi}{\cos{\theta} d\theta} + 4\int _{\frac{2\pi}{3}}^{\pi} {(\frac{1}{2} + \frac{1}{2} \cos{2\theta}) d\theta}$

$\displaystyle A = 36\int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{\frac{1}{2} (1 + \cos{2\theta}) d\theta} + 4\int _{\frac{2\pi}{3}}^{\pi}{d\theta} - 8\int _{\frac{2\pi}{3}}^{\pi}{\cos{\theta} d\theta} + 4\int _{\frac{2\pi}{3}}^{\pi}{\frac{1}{2}}{(1 + \cos{2\theta}) d\theta}$

$\displaystyle A = \frac{36}{2} \int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{(1 + \cos{2\theta}) \ d\theta} + 4\int _{\frac{2\pi}{3}}^{\pi}{d\theta} - 8\int _{\frac{2\pi}{3}}^{\pi}{\cos{\theta} \ d\theta} + \frac{4}{2} \int_{\frac{2\pi}{3}}^{\pi}{(1 + \cos{2\theta}) \ d\theta}$

$\displaystyle A = 18\int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{(1 + cos{2\theta}) \ d\theta} + 4\int _{\frac{2\pi}{3}}^{\pi}{d\theta} - 8\int _{\frac{2\pi}{3}}^{\pi}{\cos{\theta} \ d\theta} + 2\int _{\frac{2\pi}{3}}^{\pi}{(1+cos{2\theta}) \ d\theta}$

$\displaystyle A = 18\int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{d\theta} + 18\int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{\cos{2\theta} \ d\theta} + 4\int _{\frac{2\pi}{3}}^{\pi}{d\theta} - 8\int _{\frac{2\pi}{3}}^{\pi}{\cos{\theta} \ d\theta} + 2\int _{\frac{2\pi}{3}}^{\pi}{d\theta} + 2\int _{\frac{2\pi}{3}}^{\pi}{\cos{2\theta} \ d\theta}$

$\displaystyle A = 18\int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{d\theta} + 18\int _{\frac{\pi}{2}}^{\frac{2\pi}{3}}{\cos{2\theta} \ d\theta} + 6\int _{\frac{2\pi}{3}}^{\pi}{d\theta} - 8\int _{\frac{2\pi}{3}}^{\pi}{\cos{\theta} \ d\theta} + 2\int _{\frac{2\int}{3}}^{\pi}{\cos{2\theta} \ d\theta}$

$\displaystyle A = 18 \left[\theta \right]_{\frac{\pi}{2}}^{\frac{2\pi}{3}} + 18 \left[\frac{1}{2} \sin{2\theta} \right]_{\frac{\pi}{2}}^{\frac{2\pi}{3}} + 6\left[\theta \right]_{\frac{2\pi}{3}}^{\pi} - 8 \left[\sin{\theta} \right]_{\frac{2\pi}{3}}^{\pi} + 2 \left[\frac{1}{2} \sin{2\theta} \right]_{\frac{2\pi}{3}}^{\pi}$

$\displaystyle A = 18 \left[\theta \right]_{\frac{\pi}{2}}^{\frac{2\pi}{3}} + 18(\frac{1}{2}) \left[\sin{2\theta} \right]_{\frac{\pi}{2}}^{\frac{2\pi}{3}} + 6 \left[\theta \right]_{\frac{2\pi}{3}}^{\pi} - 8 \left[\sin{\theta} \right]_{\frac{2\pi}{3}}^{\pi} + 2(\frac{1}{2}) \left[\sin{2\theta} \right]_{\frac{2\pi}{3}}^{\pi}$

$\displaystyle A = 18 \left[\theta \right]_{\frac{\pi}{2}}^{\frac{2\pi}{3}} + 9 \left[\sin{2\theta} \right]_{\frac{\pi}{2}}^{\frac{2\pi}{3}} + 6 \left[\theta \right]_{\frac{2\pi}{3}}^{\pi} - 8 \left[\sin{\theta} \right]_{\frac{2\pi}{3}}^{\pi} + \left[\sin{2\theta} \right]_{\frac{2\pi}{3}}^{\pi}$

$\displaystyle A = 18 \left(\frac{2\pi}{3} - \frac{\pi}{2} \right) + 9 \left[\sin{2 \left(\frac{2\pi}{3} \right)} - \sin{2 \left(\frac{\pi}{2} \right)} \right] + 6 \left(\pi - \frac{2\pi}{3} \right) - 8 \left(\sin{\pi} - \sin{\frac{2\pi}{3}} \right) + \left[\sin{2\pi} - \sin{2 \left(\frac{2\pi}{3} \right)} \right]$

$\displaystyle A = 18 \left(\frac{\pi}{6} \right) + 9 \left(\sin{\frac{4\pi}{3}} - \sin{\pi} \right) + 6 \left(\frac{\pi}{3} \right) - 8 \left(\sin{\pi} - \sin{\frac{2\pi}{3}} \right) + \left(\sin{2\pi} - \sin{\frac{4\pi}{3}} \right)$

$\displaystyle A = 3\pi + 9 \left(-\frac{\sqrt{3}}{2} - 0 \right) + 2\pi - 8 \left(0 - \frac{\sqrt{3}}{2} \right) + 0 - \left(-\frac{\sqrt{3}}{2} \right)$