Longitud de arco de una curva polar. Cálculo vectorial.

Introducción

Sea f una función cuya derivada es continua en un intervalo $\alpha \le \theta \le \beta$ . La longitud de la gráfica de $r = f(\theta)$ , desde $\theta=\alpha$ hasta $\theta = \beta$ es

$\displaystyle s = \int _{\alpha}^{\beta}{\sqrt{{f(\theta)}^{2} + {[{f}^{'}(\theta)}]^2} d\theta} = \int _{\alpha}^{\beta}{\sqrt{r^2 + {(\frac{dr}{d\theta})}^{2}} d\theta}$

Problemas resueltos

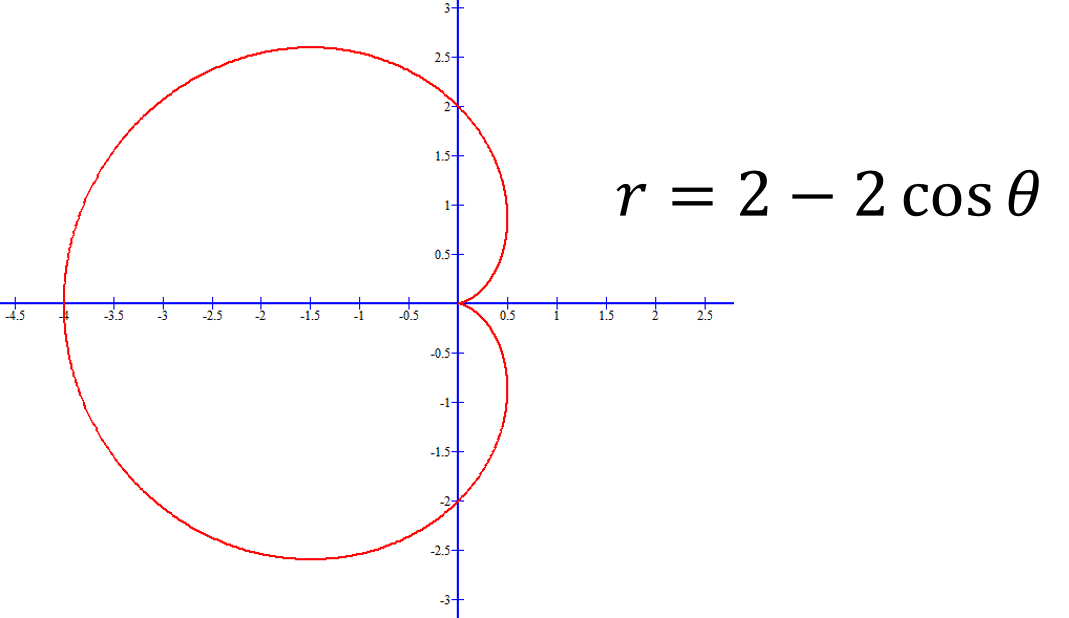
Problema 1. Encontrar la longitud de una curva polar $r = 1 + \sin{\theta}$ , en el intervalo $0 \le \theta \le 2\pi$

Solución. Se deriva la función con respecto a la variable independiente

$r = 1 + \sin{\theta}$

$\displaystyle \frac{dr}{d\theta} = \cos{\theta}$

Luego, en el intervalo, $0 \le \theta \le 2\pi$ , se tiene que $\alpha = 0$ y $\beta = 2\pi$ . Más tarde, sustituyendo en la fórmula de la longitud de arco

$\displaystyle s = \int _{\alpha}^{\beta}{\sqrt{r^2 + {\left(\frac{dr}{d\theta} \right)}^{2}} \ d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{{(1+\sin{\theta})}^2 + {(\cos{\theta})}^{2}} \ d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{(1+2 \sin{\theta} + \sin^2{\theta}) + \cos^2{\theta}} \ d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{1+2 \sin{\theta} + \sin^2{\theta} + \cos^2{\theta}} \ d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{1+2 \sin{\theta} + 1} \ d\theta} = \int _{0}^{2\pi}{\sqrt{2+2 \sin{\theta}} \ d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{2(1+ \sin{\theta})} \ d\theta} = \int _{0}^{2\pi}{\sqrt{2} \sqrt{1+ \sin{\theta}} \ d\theta}$

$\displaystyle s = \sqrt{2} \int _{0}^{2\pi}{\sqrt{1+ \sin{\theta}} \ d\theta}$

Graficando la función

Figura 1. Graficando la función polar $r = 1 + \sin{\theta}$ .

Se observa que el recorrido de la función se puede considerar desde $\displaystyle \frac{\pi}{2}$ (para $\alpha$ ) hasta $\displaystyle \frac{3\pi}{2}$ (para $\beta$ ). Entonces, realizando una modificación, resulta que

$\displaystyle s = \sqrt{2} \int _{0}^{2\pi}{\sqrt{1+ \sin{\theta}} \ d\theta} = 2 \sqrt{2} \int _{-\frac{\pi}{2}}^{\frac{\pi}{2}}{\sqrt{1+ \sin{\theta}} \ d\theta}$

Resolviendo la integral como una integral indefinida

$\displaystyle \int {\sqrt{1+ \sin{\theta}} \ d\theta}$

tomando lo siguiente

Aplicando el método de sustitución

$\displaystyle \int {\sqrt{1+ \sin{\theta}} \ d\theta} = \int{\sqrt{1+ h} \ \frac{dh}{\sqrt{1-h^2}}}$

$\displaystyle \int {\sqrt{1+ \sin{\theta}} \ d\theta} = \int{\sqrt{1+ h} \ \frac{dh}{\sqrt{1+ h} \sqrt{1-h}}}$

$\displaystyle \int {\sqrt{1+ \sin{\theta}} \ d\theta} = \int{\frac{dh}{\sqrt{1-h}}} = - 2 \sqrt{1-h}$

$\displaystyle \int {\sqrt{1+ \sin{\theta}} \ d\theta} = - 2 \sqrt{1-\sin{\theta}}$

Entonces

$\displaystyle s = 2 \sqrt{2} \int _{-\frac{\pi}{2}}^{\frac{\pi}{2}}{\sqrt{1+ \sin{\theta}} \ d\theta}$

$\displaystyle s = 2 \sqrt{2} \left[- 2 \sqrt{1-\sin{\theta}} \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$

$\displaystyle s = -4 \sqrt{2} \left[\sqrt{1-\sin{\theta}} \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$

$\displaystyle s = -4 \sqrt{2} \left[\sqrt{1-\sin{\frac{\pi}{2}}} - \sqrt{1-\sin{\left(-\frac{\pi}{2} \right)}} \right]$

$\displaystyle s = -4 \sqrt{2} \left(\sqrt{1-1} - \sqrt{1+1} \right)$

$\displaystyle s = -4 \sqrt{2} \left[\sqrt{0} - \sqrt{2} \right]$

$\displaystyle s = -4 \sqrt{2} \left(0 - \sqrt{2} \right) = 8$

Finalmente, el área encontrada es

$\displaystyle \therefore s = 8 \ \text{u}^2$

Problema 2. Encontrar la longitud de una curva polar $r = 2 - 2\cos{\theta}$ , en el intervalo $[0, 2\pi]$

Solución. Se deriva la función con respecto a la variable independiente

$r = 2 - 2\cos{\theta}$

$\displaystyle \frac{dr}{d\theta} = 2\sin{\theta}$

Sustituyendo en la fórmula de la longitud de arco

$\displaystyle s = \int _{\alpha}^{\beta}{\sqrt{r^2 + {\left(\frac{dr}{d\theta} \right)}^{2}} d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{{(2 - 2\cos{\theta})}^{2} + {(2\sin{\theta})}^{2}} d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{4 - 8\cos{\theta} + 4{\cos}^{2}{\theta} + 4{\sin}^{2}{\theta}} d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{4 - 8\cos{\theta} + 4({\cos}^{2}{\theta} + {\sin}^{2}{\theta})} d\theta}$

Recordando que ${\cos}^{2}{\theta} + {\sin}^{2}{\theta} = 1$ , aplicándolo en la integral

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{4 - 8\cos{\theta} + 4({\cos}^{2}{\theta} + {\sin}^{2}{\theta})} d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{4 - 8\cos{\theta} + 4(1)} d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{4 - 8\cos{\theta} + 4} d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{8-8\cos{\theta}} d\theta}$

$\displaystyle s = \int _{0}^{2\pi}{\sqrt{8(1 - \cos{\theta})} d\theta}$

$\displaystyle s = \sqrt{8} \int _{0}^{2\pi}{\sqrt{1- \cos{\theta}} d\theta}$

Antes de continuar, de la identidad trigonométrica $\displaystyle {\sin}^{2}{\theta} = \frac{1}{2} - \frac{1}{2} \cos{2\theta}$ , se aplica esta identidad para la mitad de un ángulo, es decir, $\displaystyle \theta \rightarrow \frac{\theta}{2}$ , entonces, se tiene lo siguiente

$\displaystyle {\sin}^{2}{\frac{\theta}{2}} = \frac{1}{2} - \frac{1}{2} \cos{\left[(2) \left(\frac{\theta}{2} \right)\right]} = \frac{1}{2} - \frac{1}{2} \cos{\theta}$

Se despeja el término $1 - \cos{\theta}$

$\displaystyle {\left(\sin{\frac{\theta}{2}}\right)}^{2} = \frac{1}{2} - \frac{1}{2} \cos{\theta}$

$\displaystyle {\left(\sin{\frac{\theta}{2}}\right)}^{2} = \frac{1}{2}(1 - \cos{\theta})$

$\displaystyle 2{\left(\sin{\frac{\theta}{2}}\right)}^{2} = 1 - \cos{\theta}$

$\displaystyle 1 - \cos{\theta} = 2{\left(\sin{\frac{\theta}{2}}\right)}^{2}$

Continuando

$\displaystyle s = \sqrt{8} \int _{0}^{2\pi}{\sqrt{1- \cos{\theta}} d\theta}$

$\displaystyle s =\sqrt{8} \int _{0}^{2\pi}{\sqrt{2{\left(\sin{\frac{\theta}{2}}\right)}^{2}} d\theta} = \sqrt{8} \int _{0}^{2\pi}{\sqrt{2}\sqrt{{\left(\sin{\frac{\theta}{2}}\right)}^{2}} d\theta}$

$\displaystyle s =\sqrt{8}\sqrt{2} \int _{0}^{2\pi}{\sin{\frac{\theta}{2}} \ d\theta} = \sqrt{16} \int _{0}^{2\pi}{\sin{\frac{\theta}{2}} \ d\theta}$

$\displaystyle s =4 \int _{0}^{2\pi}{\sin{\frac{\theta}{2}} d\theta}$

Esta integral, dentro de la función trigonométrica del seno, se aplica el método de sustitución, donde se asigna $\displaystyle z = \frac{\theta}{2}$ . Entonces