Transformación de coordenadas polares a rectangulares y viceversa. Cálculo vectorial.

Las coordenadas polares (r, θ) de un punto están relacionadas con las coordenadas rectangulares (x, y) de ese punto como sigue.

Problema 1. Convertir las siguientes coordenadas polares a coordenadas rectangulares.

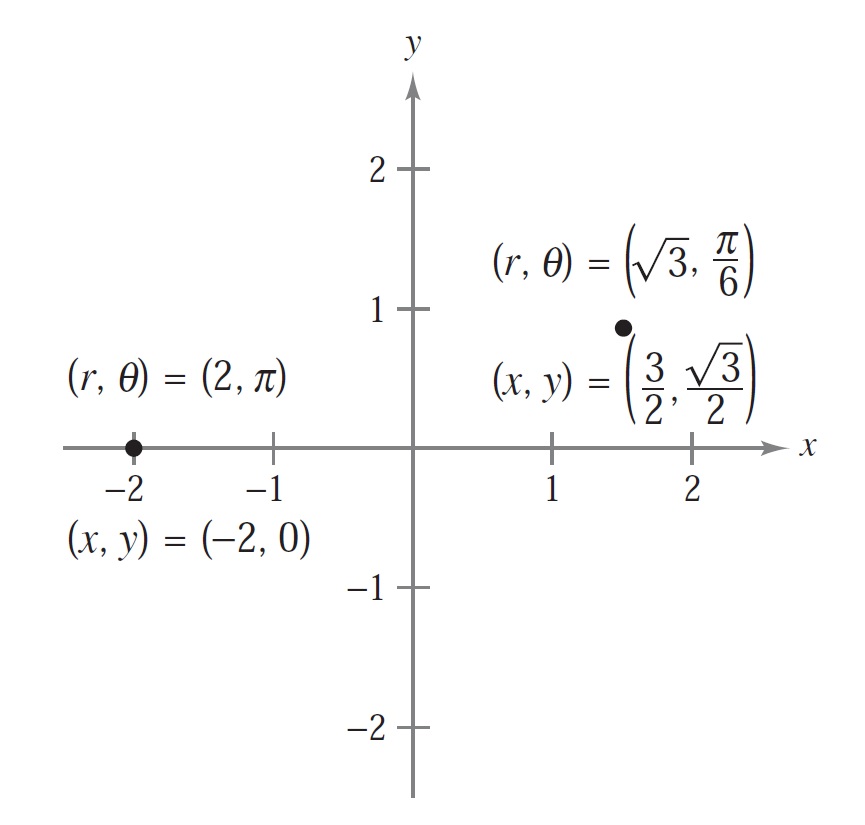
a) (2, π).

Solución. Se determinan los valores correspondientes para obtener las coordenadas rectangulares.

Por tanto, la coordenada rectangular encontrada es $(-2, 0)$

b) (√3,π/6)

Solución. Se determinan los valores correspondientes para obtener las coordenadas rectangulares.

La coordenada rectangular encontrada es $\displaystyle (\frac{3}{2}, \frac{\sqrt{3}}{2})$ .

Problema 2. Convertir de coordenadas rectangulares a coordenadas polares para las siguientes:

a) (1, 1)

Solución. Se determinan los valores correspondientes para obtener las coordenadas polares.

Por lo tanto, la coordenada polar encontrada es $\displaystyle (\frac{3}{4} \pi, \sqrt{2})$ .

b) (0, 2)

Solución. Se determinan los valores correspondientes para obtener las coordenadas polares.

La coordenada polar encontrada es $\displaystyle (2, \frac{\pi}{2})$ .

Coordenadas rectangulares	Coordenadas polares
$x = r \cos{\theta}$	$\displaystyle r = \sqrt{x^2 + y^2}$
$y = r \sin{\theta}$	$\displaystyle \theta = \arctan{(\frac{y}{x})} = {\tan}^{(-1)}{(\frac{y}{x})}$

Para el valor de $\theta$	Para el valor de la magnitud de $r$
$\displaystyle \tan{\theta} = \frac{y}{x}$	$\displaystyle r = \sqrt{x^2+y^2}$
$\displaystyle \tan{\theta} = \frac{1}{-1}$	$\displaystyle r = \sqrt{1^2+(-1)^2}$
$\displaystyle \theta = \arctan{(-1)} = - \frac{\pi}{4} = - \frac{\pi}{4} + \pi$	$\displaystyle r = \sqrt{2}$
$\displaystyle \theta = \frac{3}{4} \pi$

Para el valor de $\theta$	Para el valor de la magnitud de $r$
$\displaystyle \tan{\theta} = \frac{y}{x}$	$\displaystyle r = \sqrt{x^2+y^2}$
$\displaystyle \tan{\theta} = \frac{2}{0} = \infty$	$\displaystyle r = \sqrt{0^2+2^2} = 2$
$\displaystyle \theta = \arctan{(\infty)}$	$\displaystyle r = 2$
$\displaystyle \theta = \frac{\pi}{2}$

Publicado por Cesar Reyes