Velocidad y aceleración. Primera parte. Cálculo vectorial.

Introducción

El vector posición se representa como:

$\displaystyle \overrightarrow{r}(t) = x(t) \overrightarrow{i} + y(t) \overrightarrow{j}$

Velocidad y aceleración

Si x y y son funciones de t que tienen primera y segunda derivada y $\overrightarrow{r}$ es una función vectorial dada por $\overrightarrow{r}(t) = x(t)\overrightarrow{i} + y(t) \overrightarrow{j}$ , entonces el vector velocidad, el vector aceleración y la rapidez en el instante t se definen como:

$\overrightarrow{r}(t) = x(t) \overrightarrow{i} + y(t) \overrightarrow{j}$

$\overrightarrow{v}(t) = {\overrightarrow{r}}^{'} (t) = {x}^{'} (t) \overrightarrow{i} + {y}^{'}(t) \overrightarrow{j}$

$\overrightarrow{a}(t) = {\overrightarrow{r}}^{''}(t) = {\overrightarrow{v}}^{'} (t) = {x}^{''}(t) \overrightarrow{i} + {y}^{''}(t) \overrightarrow{j}$

$\displaystyle ||\overrightarrow{v}|| = ||\overrightarrow{r}^{'} (t)|| = \sqrt{{[{x}^{'}(t)]}^{2} + {[{y}^{'}(t)]}^{2}}$

NOTA. Se utilizará estas fórmulas para curvas en el espacio con solo agregar $z(t)$ , ${z}^{'}(t)$ , ${z}^{''}(t)$ , es decir:

$\overrightarrow{r}(t) = x(t) \overrightarrow{i} + y(t) \overrightarrow{j} + z(t) \overrightarrow{k}$

$\overrightarrow{v}(t) = {\overrightarrow{r}}^{'}(t) = {x}^{'}(t) \overrightarrow{i} + {y}^{'}(t) \overrightarrow{j} + {z}^{'}(t) \overrightarrow{k}$

$\overrightarrow{a}(t) = {\overrightarrow{r}}^{''}(t) = {\overrightarrow{v}}^{'}(t) = {x}^{''}(t) \overrightarrow{i} + {y}^{''}(t) \overrightarrow{j} + {z}^{''}(t) \overrightarrow{k}$

$\displaystyle ||\overrightarrow{v}|| = ||{\overrightarrow{r}}^{'}(t)|| = \sqrt{{[{x}^{'}(t)]}^{2} + {[y(t)]}^{2} + {[z(t)]}^{2}}$

Problemas resueltos

Problema 1. Hallar la velocidad y aceleración a lo largo de una curva dada:

$\overrightarrow{r}(t) = 2 \sin{\frac{t}{2}} \overrightarrow{i} + 2 \cos{\frac{t}{2}} \overrightarrow{j}$

Solución. Para obtener la función vectorial de la velocidad, se deriva, una vez, la función vectorial con respecto a $t$

$\displaystyle \overrightarrow{v}(t) = {\overrightarrow{r}}^{'}(t) = [\frac{d}{dt} (2 \sin{\frac{t}{2}})] \overrightarrow{i} + [2 \cos{\frac{t}{2}}] \overrightarrow{j}$

$\displaystyle \overrightarrow{v}(t) = 2(\frac{1}{2}) \cos{\frac{t}{2}} \overrightarrow{i} + 2(\frac{1}{2})(-\sin{\frac{t}{2}}) \overrightarrow{j}$

$\displaystyle \overrightarrow{v}(t) = \cos{\frac{t}{2}} \overrightarrow{i} - \sin{\frac{t}{2}} \overrightarrow{j}$

Y para obtener la función vectorial de la aceleración, se deriva la función vectorial de la velocidad, una vez, con respecto a $t$

$\displaystyle \overrightarrow{a}(t) = {\overrightarrow{v}}^{'} (t)$

$\displaystyle \overrightarrow{a}(t) = \frac{d}{dt} (\cos{\frac{t}{2}}) \overrightarrow{i} - \frac{d}{dt} (\sin{\frac{t}{2}}) \overrightarrow{j}$

$\displaystyle \overrightarrow{a}(t) = -(\frac{1}{2} \sin{\frac{t}{2}}) \overrightarrow{i} - (\frac{1}{2} \cos{\frac{t}{2}}) \overrightarrow{j}$

Para obtener la rapidez, se calcula la magnitud de la función vectorial de la velocidad:

$\displaystyle ||\overrightarrow{v}(t)|| = \sqrt{{[x(t)]}^{2} + {[y(t)]}^{2}}$

$\displaystyle ||\overrightarrow{v}(t)|| = \sqrt{{(-\frac{1}{2} \sin{\frac{t}{2}})}^{2} + {(-\frac{1}{2} \cos{\frac{t}{2}})}^{2}} = \sqrt{\frac{1}{4} {(\sin{\frac{t}{2}})}^{2} + \frac{1}{4} {(\cos{\frac{t}{2}})}^{2}}$

$\displaystyle ||\overrightarrow{v}(t)|| = \sqrt{{(\sin{\frac{t}{2}})}^{2} + {(\cos{\frac{t}{2}})}^{2}} = \sqrt{1}$

$\displaystyle ||\overrightarrow{v}(t)|| = 1$

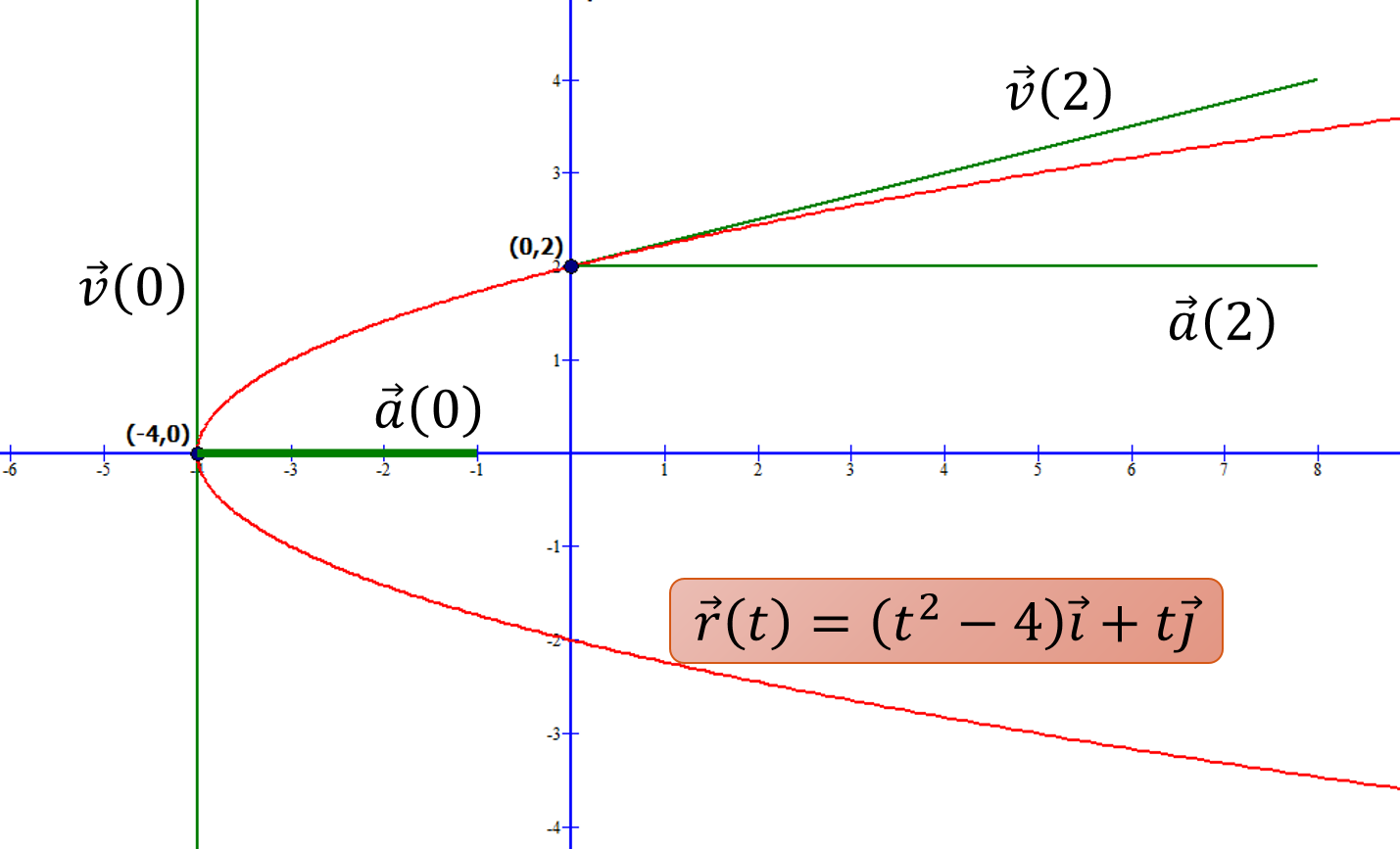
Problema 2. Dibujar de los vectores velocidad y aceleración en el plano

$\overrightarrow{r}(t) = (t^2-4) \overrightarrow{i} + t \overrightarrow{j}$

para t=0 y t=2.

Solución. De la función vectorial posición

$\overrightarrow{r}(t) = (t^2 - 4) \overrightarrow{i} + t \overrightarrow{j}$

Se deriva una vez con respecto a $t$ para obtener la función vectorial de la velocidad

$\displaystyle \overrightarrow{v}(t) = \frac{d\overrightarrow{r}}{dt}$

$\displaystyle \overrightarrow{v}(t) = \frac{d}{dt} [(t^2-4) \overrightarrow{i} + t \overrightarrow{j}]$

$\displaystyle \overrightarrow{v}(t) = [\frac{d}{dt} (t^2-4)] \overrightarrow{i} + [\frac{d}{dt} (t)] \overrightarrow{j}$

$\overrightarrow{v}(t) = 2t \overrightarrow{i} + \overrightarrow{j}$

Y se deriva una vez, este último resultado, con respecto a $t$ para obtener la función vectorial de la aceleración

$\displaystyle \overrightarrow{a}(t) = \frac{d \overrightarrow{v}}{dt}$

$\displaystyle \overrightarrow{a}(t) = \frac{d}{dt} [2t \overrightarrow{i} + \overrightarrow{j}]$

$\displaystyle \overrightarrow{a}(t) = [\frac{d}{dt} (2t)] \overrightarrow{i} + [\frac{d}{dt} (1)] \overrightarrow{j}$

$\overrightarrow{a}(t) = 2\overrightarrow{i} + 0\overrightarrow{j}$

Para $t=0$ , en el caso del vector velocidad

$\displaystyle \overrightarrow{v}(t) = 2t \overrightarrow{i} + \overrightarrow{j}$

$\overrightarrow{v}(0) = 2(0) \overrightarrow{i} + \overrightarrow{j}$

$\overrightarrow{v}(0) = 0\overrightarrow{i} + \overrightarrow{j}$

Y para el vector aceleración

$\overrightarrow{a}(t) = 2\overrightarrow{i} + 0\overrightarrow{j}$

$\overrightarrow{a}(0) = 2\overrightarrow{i} + 0\overrightarrow{j}$

Para $t=2$ , para el vector velocidad

$\overrightarrow{v}(t) = 2t \overrightarrow{i} + \overrightarrow{j}$

$\overrightarrow{v}(2) = 2(2) \overrightarrow{i} + \overrightarrow{j}$

$\overrightarrow{v}(2) = 4\overrightarrow{i} + \overrightarrow{j}$

Y para el vector aceleración

$\overrightarrow{a}(t) = 2\overrightarrow{i} + 0\overrightarrow{j}$

$\overrightarrow{a}(2) = 2\overrightarrow{i} + 0\overrightarrow{j}$

También, para el vector posición

$\overrightarrow{r}(t) = x(t) \overrightarrow{i} + y(t) \overrightarrow{j}$

$\overrightarrow{r}(t) = (t^2 - 4) \overrightarrow{i} + t \overrightarrow{j}$

donde $x(t) = t^2 - 4$ y $y(t) = t$ .

Para $t=0$ , sustituyéndolo en $x(t)$

$x(t) = t^2 - 4$

$x(0) = 0^2 - 4 = 0 - 4$

$x(0) = -4$

Y sustituyéndolo en $y(t)$

$y(0) = 0$

Por lo tanto, cuando $t=0$ , los vectores velocidad y aceleración estarán ubicados en el punto $(-4,0)$ .

Para $t=2$ , sustituyéndolo en $x(t)$

$x(t) = t^2 - 4$

$x(2) = 2^2 - 4 = 4 - 4$

$x(2) = 0$

Y sustituyéndolo en $y(t)$

$y(2) = 2$

Por lo tanto, cuando $t=2$ , los vectores velocidad y aceleración estarán ubicados en el punto $(0,2)$ .

Imagen1 — *Figura 1. Representación gráfica de los vectores velocidad y aceleración para la función vectorial « $\overrightarrow{r}(t)=(t^2-4) \overrightarrow{i} + t\overrightarrow{j}$ «.*

*Figura 1. Representación gráfica de los vectores velocidad y aceleración para la función vectorial « $\overrightarrow{r}(t)=(t^2-4) \overrightarrow{i} + t\overrightarrow{j}$ «.*

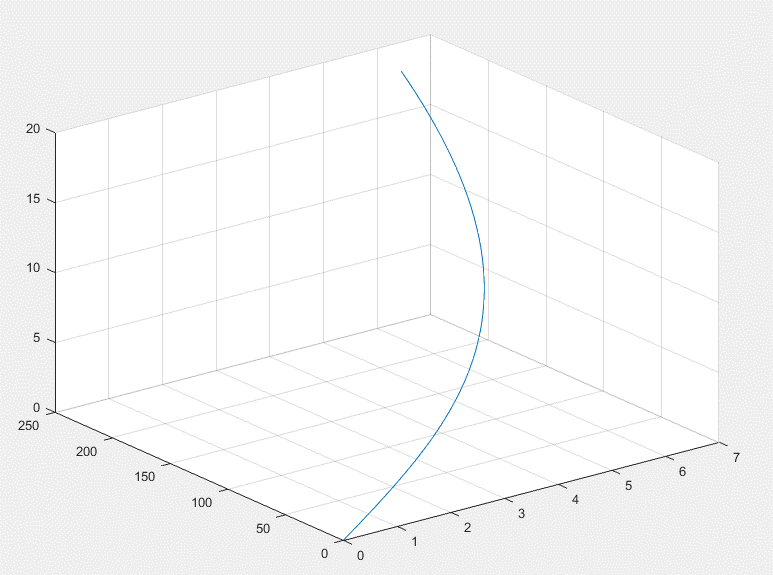
Problema 3. Dibuje de los vectores velocidad y aceleración en el espacio para

$\overrightarrow{r}(t) = t \overrightarrow{i} + t^3 \overrightarrow{j} + 3t \overrightarrow{k}$

donde $t \ge 0$ para $t=1$ .

Solución. Para la obtener la función vectorial de la velocidad, se deriva la función vectorial con respecto a $t$ en ambos miembros

$\displaystyle \overrightarrow{v}(t) = \frac{d \overrightarrow{r}}{dt} = \frac{d}{dt} [t \overrightarrow{i} + t^3 \overrightarrow{j} + 3t \overrightarrow{k}]$

$\displaystyle \overrightarrow{v}(t) = [\frac{d}{dt} (t)] \overrightarrow{i} + [\frac{d}{dt} (t^3 )] \overrightarrow{j} + [\frac{d}{dt} (3t)] \overrightarrow{k}$

$\overrightarrow{v}(t) = \overrightarrow{i} + 3t^2 \overrightarrow{j} + 3 \overrightarrow{k}$

Si $t=1$ y sustituyéndolo en la función vectorial de la velocidad

$\overrightarrow{v}(t) = \overrightarrow{i} + 3t^2 \overrightarrow{j} + 3 \overrightarrow{k}$

$\overrightarrow{v}(1) = \overrightarrow{i} + 3(1)^2 \overrightarrow{j} + 3 \overrightarrow{k}$

$\overrightarrow{v}(1) = \overrightarrow{i} + 3 \overrightarrow{j} + 3 \overrightarrow{k}$

Para obtener la función vectorial de la aceleración, se deriva una vez con respecto a $t$ la función vectorial de la velocidad

$\displaystyle \overrightarrow{a}(t) = \frac{d\overrightarrow{v}}{dt} = \frac{d}{dt} [\overrightarrow{i} + 3t^2 \overrightarrow{j} + 3 \overrightarrow{k}]$

$\displaystyle \overrightarrow{a}(t) = [\frac{d}{dt} (1)] \overrightarrow{i} + [\frac{d}{dt} (3t^2 )] \overrightarrow{j} + [\frac{d}{dt} (3)] \overrightarrow{k}$

$\overrightarrow{a}(t) = 0\overrightarrow{i} + 6t \overrightarrow{j} + 0 \overrightarrow{k}$

Si $t=1$ y sustituyéndolo en la función vectorial de la aceleración

$\overrightarrow{a}(t) = 0 \overrightarrow{i} + 6t \overrightarrow{j} + 0 \overrightarrow{k}$

$\overrightarrow{a}(1) = 0\overrightarrow{i} + 6(1) \overrightarrow{j} + 0\overrightarrow{k}$

$\overrightarrow{a}(1) = 0\overrightarrow{i} + 6 \overrightarrow{j} + 0 \overrightarrow{k}$

Para la función vectorial de la posición

$\overrightarrow{r}(t) = x(t) \overrightarrow{i} + y(t) \overrightarrow{j} + z(t) \overrightarrow{k}$

$\overrightarrow{r}t) = t \overrightarrow{i} + t^3 \overrightarrow{j} + 3t \overrightarrow{k}$

Se observa que $x(t) = t$ , $y(t)=t^3$ , $z(t)=3t$ .

Para $t=1$ , se sustituye en las ecuaciones paramétricas de la función vectorial de la posición

$x(t)=t$

$x(1) = 1$

$y(t)=t^3$

$y(1)=1^3$

$y(1)=1$

$z(t)=3t$

$z(1)=3(1)$

$z(1)=3$

Por lo tanto, en $t=1$ , los vectores velocidad y posición estarán ubicados en la coordenada $(1,1,3)$ .

Imagen2 — *Figura 2. Representación gráfica de la función vectorial $\overrightarrow{r}(t) = t \overrightarrow{i} + t^3 \overrightarrow{j} + 3t \overrightarrow{k}$ .*

*Figura 2. Representación gráfica de la función vectorial $\overrightarrow{r}(t) = t \overrightarrow{i} + t^3 \overrightarrow{j} + 3t \overrightarrow{k}$ .*

Problema 4. Hallar una función posición por integración para

$P(1, 2, 0)$ y $\overrightarrow{a}(t) = \overrightarrow{j} + 2\overrightarrow{k}$

en $t=2$ .

Solución. Utilizando $P(1, 2, 0)$ y expresándolo en función vectorial simulando cuando $t=0$

$\overrightarrow{r}(t) = x(t) \overrightarrow{i} + y(t) \overrightarrow{j} + z(t) \overrightarrow{k}$

$\overrightarrow{r}(0) = x(0) \overrightarrow{i} + y(0) \overrightarrow{j}+ z(0) \overrightarrow{k}$

$\overrightarrow{r}(0) = \overrightarrow{i} + 2 \overrightarrow{j} + 0 \overrightarrow{k}$

Entonces, partiendo de la aceleración y despejando la diferencial del vector de la velocidad

$\displaystyle \overrightarrow{a}(t) = \frac{d\overrightarrow{v}}{dt}$

$\displaystyle \frac{d\overrightarrow{v}}{dt} = \overrightarrow{a}(t)$

$\overrightarrow{v} = \overrightarrow{a}(t) dt$

$\displaystyle \int{dv} = \int {\overrightarrow{a}(t) dt}$

$\displaystyle \overrightarrow{v}(t) = \int {\overrightarrow{a}(t) dt}$

$\displaystyle \overrightarrow{v}(t) = \int {(\overrightarrow{j} + 2 \overrightarrow{k}) dt}$

$\displaystyle \overrightarrow{v}(t) = [\int {dt}] \overrightarrow{j} + [2\int{dt}] \overrightarrow{k}$

$\displaystyle \overrightarrow{v}(t) = [0 \int {dt}] \overrightarrow{i} + [\int{dt}] \overrightarrow{j} + [2\int {dt}] \overrightarrow{k}$

$\overrightarrow{v}(t) = C_1 \overrightarrow{i} + (t + C_2) \overrightarrow{j} + (2t + C_3) \overrightarrow{k}$

Si $\overrightarrow{v}(0) = \overrightarrow{0} = 0 \overrightarrow{i} + 0 \overrightarrow{j} + 0 \overrightarrow{k}$

$\overrightarrow{v}(0) = C_1 \overrightarrow{i} + (0 + C_2) \overrightarrow{j} + (0 + C_3) \overrightarrow{k}$

$\overrightarrow{0} = C_1 \overrightarrow{i} + (0 + C_2) \overrightarrow{j} + (0 + C_3) \overrightarrow{k}$

$0 \overrightarrow{i} + 0\overrightarrow{j} + 0\overrightarrow{k} = C_1 \overrightarrow{i} + (0+C_2 ) \overrightarrow{j} + (0+C_3) \overrightarrow{k}$

Entonces, las ecuaciones al ser resueltas son

$0 = {C}_{1}$

${C}_{1} = 0$

$0 = 0 + C_2$

${C}_{2} = 0$

$0 = 0 + C_3$

${C}_{3} = 0$

Sustituyendo en el resultado de la velocidad

$\displaystyle \overrightarrow{v}(t) = 0\overrightarrow{i} + (t+C_1) \overrightarrow{j} + (2t+C_2) \overrightarrow{k}$

$\overrightarrow{v}(t) = 0\overrightarrow{i} + t \overrightarrow{j} + 2t \overrightarrow{k}$

Ahora

$\displaystyle \frac{d\overrightarrow{r}}{dt} = \overrightarrow{v}(t)$

$d \overrightarrow{r} = \overrightarrow{v}(t) \ dt$

$\displaystyle \int {d\overrightarrow{r}} = \int{\overrightarrow{v}(t) \ dt}$

$\displaystyle \overrightarrow{r}(t) = \int {\overrightarrow{v}(t) \ dt}$

$d\overrightarrow{r}(t) = \int {(0 \overrightarrow{i} + t \overrightarrow{j} + 2t \overrightarrow{k}) \ dt}$

$\displaystyle \overrightarrow{r}(t) = [0 \int {dt}] \overrightarrow{i} + [\int{t \ dt}] \overrightarrow{j} + [2 \int{t \ dt}] \overrightarrow{k}$

$\displaystyle \overrightarrow{r}(t) = C_4 \overrightarrow{i} + (\frac{t^2}{2} + C_5) \overrightarrow{j} + 2(\frac{t^2}{2} + C_6) \overrightarrow{k}$

$\displaystyle \overrightarrow{r}(t) = C_4 \overrightarrow{i} + (\frac{t^2}{2} + C_5) \overrightarrow{j} + (t^2+C_6) \overrightarrow{k}$

Para $\overrightarrow{r}(0) = \overrightarrow{i} + 2\overrightarrow{j} + 0\overrightarrow{k}$

$\overrightarrow{r}(0) = C_4 \overrightarrow{i} + (0 + C_5) \overrightarrow{j} + (0 + C_6) \overrightarrow{k}$

$\overrightarrow{i} + 2\overrightarrow{j} + 0 \overrightarrow{k} = C_4 \overrightarrow{i} + (0+C_5) \overrightarrow{j} + (0+C_6)\overrightarrow{k}$

Igualando los términos de cada vector unitario se obtienen tres ecuaciones y al ser resueltas, se obtienen los valores de cada constante de integración

$1=C_4$