Límites y continuidad. Cálculo vectorial.

Límite de una función de dos variables

Sea f una función de dos variables definida en un disco abierto centrado en $(x_0, y_0)$ , excepto posiblemente en $(x_0, y_0)$ , y sea L un número real.

Entonces:

$\displaystyle \lim_{(x, y) \rightarrow (x_0, y_0)}{f(x, y)} = L$

Si para cada $\epsilon > 0$ existe un $\delta > 0$ tal que:

$|f(x, y) - L|< \epsilon$

Siempre que

$\displaystyle 0 < \sqrt{{(x - x_0)}^{2} + {(y - y_0)}^{2}} < \delta$

Problemas resueltos

Problema 1. Verificar un límite a partir de la definición.

$\displaystyle \lim_{(x, y) \rightarrow (a, b)}{x} = a$

Solución. Comparando los parámetros

$f(x, y) = x$ y $L = a$

Por lo que, se necesita mostrar que para cada $\epsilon > 0$ , existe un entorno $\delta$ de $(a,b)$ tal que $|f(x,y)-L|<\epsilon$ , es decir, $|x-a|<\epsilon$ , se observa que

$\displaystyle 0 < \sqrt{{(x-a)}^{2} + {(y-b)}^{2}}<\delta$

Lo cual implica que

$\displaystyle |f(x,y) - L| = |x-a| = \sqrt{{(x-a)}^{2})} \le \sqrt{{(x-a)}^{2} + {(y-b)}^{2}}<\delta=\epsilon$

Por lo tanto, se puede elegir $\delta=\epsilon$ , y el límite queda verificado.

Problema 2. Calcular el siguiente límite

$\displaystyle \lim_{(x,y) \rightarrow (1,2)}{\left(\frac{5x^2 y}{x^2+y^2}\right)}$

Solución. Tomando el límite en el numerador y en el denominador

$\displaystyle \lim_{(x,y) \rightarrow (1,2)}{\left(\frac{5x^2 y}{x^2+y^2}\right)} = \frac{\lim_{(x,y) \rightarrow (1,2)}{(5x^2 y)}}{\lim_{(x,y) \rightarrow (1,2)}{(x^2+y^2)}}$

Evaluando el límite

$\displaystyle \lim_{(x,y) \rightarrow (1,2)}{\left( \frac{5x^2 y}{x^2+y^2} \right)} = \left[\frac{5(1)^2 (2)}{1^2+2^2}\right] = \frac{10}{5} = 2$

Por lo tanto

$\displaystyle \therefore \lim_{(x, y) \rightarrow (1, 2)}{\left(\frac{5x^2 y}{x^2+y^2}\right)} = 2$

Problema 3. Verificar el siguiente límite

$\displaystyle \lim_{(x, y) \rightarrow (0,0)}{\left(\frac{5x^2 y}{x^2+y^2} \right)}$

Solución. Se observa que al tomar el límite del numerador y denominador, ambos se hacen cero, por lo tanto, no se puede determinar la existencia o inexistencia del límite de ambos lugares. Al graficar la función $\displaystyle f(x,y) = \frac{5x^2 y}{x^2+y^2}$ .

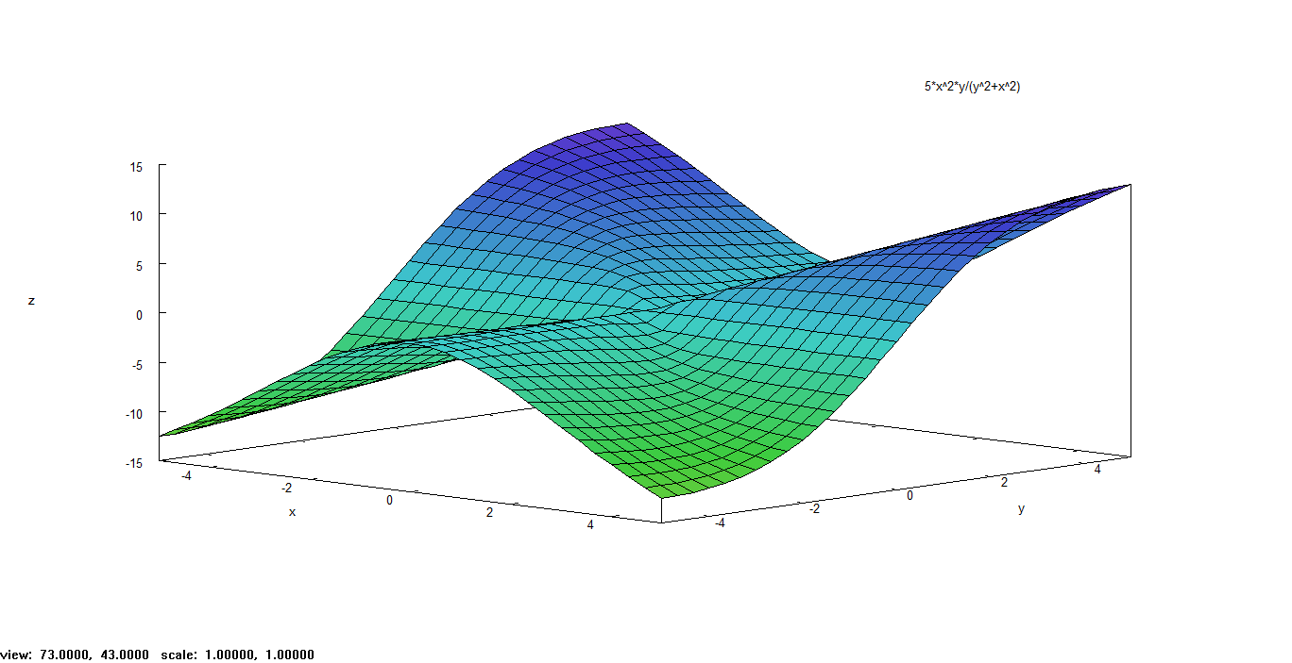
Imagen1 — *Figura 4.2.1 Representando la función f(x,y) = (5x^2y)/(x^2+y^2) en tres dimensiones.*

Analizando que, al evaluar el límite de esta función, pueda tenerse como resultado cero. Para ello, se utilizará la definición del límite, en donde $L=0$ . Comenzando, se observa que

$\displaystyle |y| \le \sqrt{x^2+y^2}$ y $\displaystyle \frac{x^2}{x^2+y^2} \le 1$

Así que, en un entorno $\delta$ de $(0,0)$ , se tiene que

$\displaystyle 0 < \sqrt{x^2+y^2} < \delta$

Lo que, para $(x,y) \ne 0$ , implica lo siguiente

$|f(x, y)-L| = |f(x, y)-0|$

$\displaystyle = |f(x,y)| = \left|\frac{5x^2 y}{x^2+y^2} \right| = 5|y|\left( \frac{x^2}{x^2+y^2} \right) \le 5|y| \le 5\sqrt{x^2+y^2} < 5\delta$

Se puede elegir (despejando $5\delta = \epsilon$ ) que $\displaystyle \delta = \frac{\epsilon}{5}$ y se concluye que

$\displaystyle \lim_{(x, y) \rightarrow (0,0)}{\left(\frac{5x^2 y}{x^2+y^2} \right)} = 0$

Problema 4. Mostrar que el límite no existe para la siguiente expresión

$\displaystyle \lim_{(x, y) \rightarrow (0,0)}{{\left(\frac{x^2-y^2}{x^2+y^2} \right)}^{2}}$

Solución. Se determina el dominio de esta función

$\displaystyle f(x,y) = {\left( \frac{x^2-y^2}{x^2+y^2} \right)}^{2}$

Donde consta de todos los puntos en el plano $xy$ con excepción del punto $(0,0)$ . Para mostrar que el límite no existe cuando $(x,y)$ se aproxime a $(0,0)$ , se considerará las aproximaciones a $(0,0)$ a lo largo de dos trayectorias diferentes [se grafica la función $f(x,y)$ ].

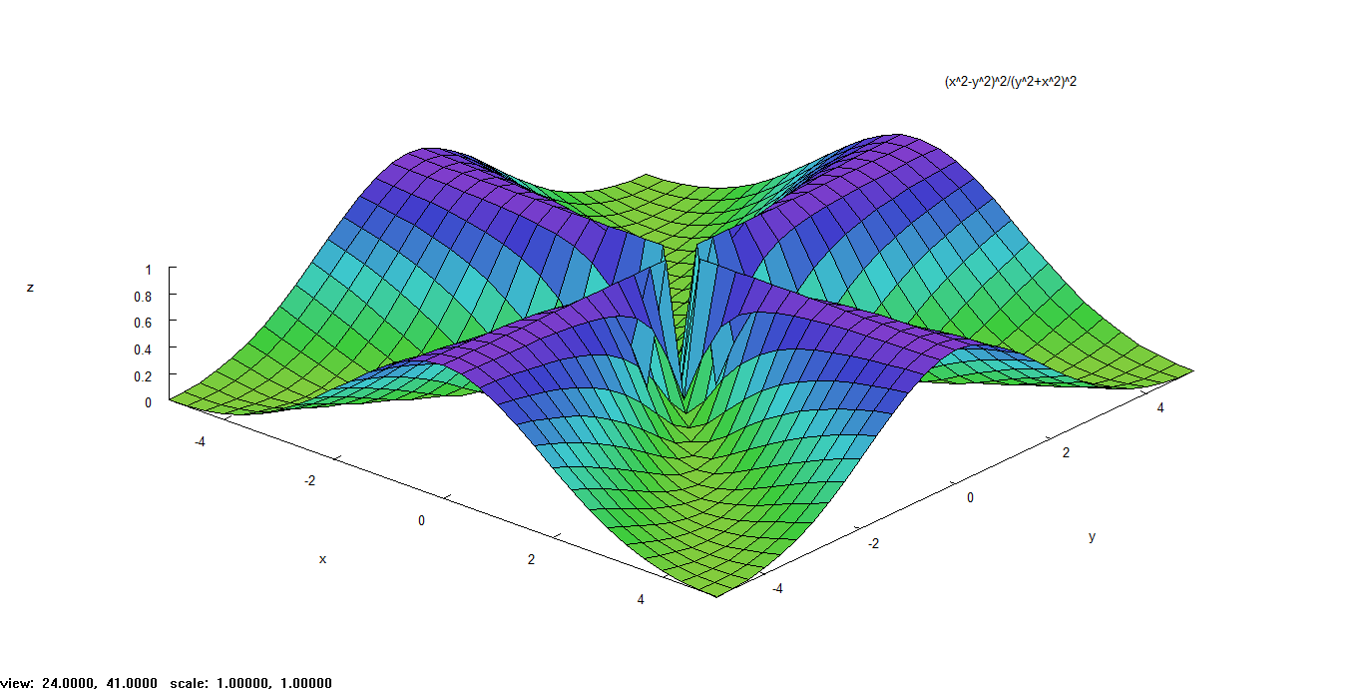
Imagen2 — *Figura 4.2.2 Representando la función f(x,y) = [(x^2-y^2)/(x^2+y^2)]^2 en tres dimensiones.*

En la gráfica, se observa que, a lo largo del eje x, todo punto es de la forma $(x,0)$ y el límite a lo largo de esta trayectoria es

$\displaystyle \lim_{(x, 0) \rightarrow (0,0)}{{\left( \frac{x^2-0^2}{x^2+0^2} \right)}^{2} } = \lim_{(x, 0) \rightarrow (0,0)}{{\left( \frac{x^2}{x^2} \right)}^{2}} = \lim_{(x,0) \rightarrow (0,0)}{{(1)}^{2}} = 1$

Sin embargo, si $(x,y)$ se aproxima a $(0,0)$ a lo largo de la recta $y=x$ , se obtiene lo siguiente

$\displaystyle \lim_{(x, x) \rightarrow (0,0)}{{\left(\frac{x^2-x^2}{x^2+x^2} \right)}^{2}} = \lim_{(x, x) \rightarrow (0,0)}{{\left(\frac{0}{2x^2}\right)}^{2}} = 0$

A lo largo del eje $y$ .

Esto significa que en cualquier disco abierto centrado en $(0,0)$ existen puntos $(x,y)$ en los que f toma el valor de uno y otros puntos en que f asume el valor de cero. Por lo tanto, se concluye que f no tiene límite cuando $(x,y) \rightarrow (0,0)$ .

Continuidad de una función de dos variables

Una función f de dos variables es continua en un punto $(x_0, y_0)$ de una región abierta $\Re$ si $f(x_0, y_0)$ es igual al límite de $f(x, y)$ cuando $(x, y) \rightarrow (x_0, y_0)$ . Es decir,

$\displaystyle \lim_{(x, y) \rightarrow (x_0, y_0)}{f(x, y)} = f(x_0, y_0)$

Funciones continuas de dos variables

Si k es un número real y f y g son funciones continuas en $(x_0, y_0)$ , entonces las funciones siguientes son continuas en $(x_0, y_0)$ .

Múltiplo escalar: $k \cdot f$
Suma y diferencia: $f \pm g$
Producto: $f \cdot g$
Cociente: $\displaystyle \frac{f}{g}$

Continuidad de una función compuesta

Si h es continua en $(x_0, y_0)$ y g es continua en $h(x_0,y_0)$ , entonces la función compuesta $(g \circ f)(x,y) = g(h(x,y))$ es continua en $(x_0, y_0)$ . Es decir:

$\displaystyle \lim_{(x, y) \rightarrow (x_0, y_0)}{g(h(x,y))} = g(h(x_0, y_0))$

Continuidad de una función de tres de variables

Una función f de tres variables es continua en un punto $(x_0, y_0, z_0)$ de una región abierta $\Re$ si $f(x_0, y_0, z_0)$ está definida y es igual al límite de $f(x, y, z)$ cuando $(x,y,z)$ se aproxima a $(x_0, y_0, z_0)$ . Es decir:

$\displaystyle \lim_{(x, y ,z) \rightarrow (x_0, y_0, z_0)}{f(x, y, z)} = f(x_0, y_0, z_0)$

Cálculo el límites y análisis de continuidad de una función

1.- $\displaystyle \lim_{(x, y) \rightarrow (2,1)}{(x+3y^2)} = 2+3{(1)}^{2} = 5$

«La función es continua en todos los puntos».

2.- $\displaystyle \lim_{(x, y) \rightarrow (2,4)}{\left(\frac{x+y}{x-y}\right)} = \frac{2+4}{2-4} = -3$

«La función es continua para $x \ne y$ «.

3.- $\displaystyle \lim_{(x, y) \rightarrow (0,1)}{\left( \frac{\arcsin{\frac{x}{y}}}{1+xy} \right)} = \frac{\arcsin{(\frac{0}{1})}}{1+(0)(1)} = 0$

«La función es continua para $xy \ne -1$ , $y \ne 0$ y $\displaystyle |\frac{x}{y}| \le 1$ «.

4.- $\displaystyle \lim_{(x, y) \rightarrow (-1,2)}{{e}^{xy}} = {e}^{-1(2)} = {e}^{-2}$

«La función es continua para todos los puntos».

5.- $\displaystyle \lim_{(x, y, z) \rightarrow (1,2, 5)}{\sqrt{x+y+z}} = \sqrt{1+2+5} = \sqrt{8}$

«La función es continua para $\displaystyle \sqrt{x+y+z} \ge 0$ «.

Referencias bibliográficas

Colley, S. J. (2013). Cálculo vectorial. México: PEARSON EDUCACIÓN.
Larson, R., & Edwards, B. (2017). Matemáticas 3. Cálculo de varias variables. México: CENGAGE Learning.
R. Spiegel, M. (1967). Análisis vectorial. México: McGRAW – HILL.

Límites y continuidad. Cálculo vectorial.

Límite de una función de dos variables

Problemas resueltos

Continuidad de una función de dos variables

Funciones continuas de dos variables

Continuidad de una función compuesta

Continuidad de una función de tres de variables

Cálculo el límites y análisis de continuidad de una función

Referencias bibliográficas

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Límites y continuidad. Cálculo vectorial.

Límite de una función de dos variables

Problemas resueltos

Continuidad de una función de dos variables

Funciones continuas de dos variables

Continuidad de una función compuesta

Continuidad de una función de tres de variables

Cálculo el límites y análisis de continuidad de una función

Referencias bibliográficas

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta