Aplicación de la regla de la cadena a velocidades o ritmos de cambio relacionados. Cálculo vectorial.

Problemas resueltos.

Problema 1. Aplicar la regla de la cadena para

$x_1 = 4 \cos{t}$ y $x_2 = 2 \sin{2t}$

$y_1 = 2\sin{t}$ y $y_2 = 3 \cos{2t}$

Para $t = \pi$ .

Solución. Se utiliza la siguiente ecuación

$\displaystyle \frac{\partial s}{\partial t} = \frac{ds}{dx_1} \frac{dx_1}{dt} + \frac{ds}{dx_2} \frac{dx_2}{dt} + \frac{ds}{dy_1} \frac{dy_1}{dt} + \frac{ds}{dy_2} \frac{dy_2}{dt}$

Pero antes se hace lo siguiente. Si $t=\pi$

$x_1 = 4 \cos{\pi} = 4(-1) = -4$

$x_2 = 2 \sin{2(\pi)} = 2 \sin{2\pi} = 2(0) = 0$

$y_1 = 2 \sin{\pi} = 2(0) = 0$

$y_2 = 3 \cos{2(\pi)} = 3 \cos{2\pi} = 3(1) = 3$

La fórmula para la distancia entre objetos es

$\displaystyle s = \sqrt{{(x_2 - x_1)}^{2} + {(y_2-y_1)}^{2}}$

Y tomando los valores de $x_1$ , $x_2$ , $y_1$ y $y_2$ en la fórmula de la distancia

$\displaystyle s = \sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}} = \sqrt{{(0+4)}^{2} + {(3-0)}^{2}}$

$\displaystyle s = \sqrt{{(4)}^{2} + {(3)}^{2}} = \sqrt{16+9} = \sqrt{25}$

$\therefore s=5$

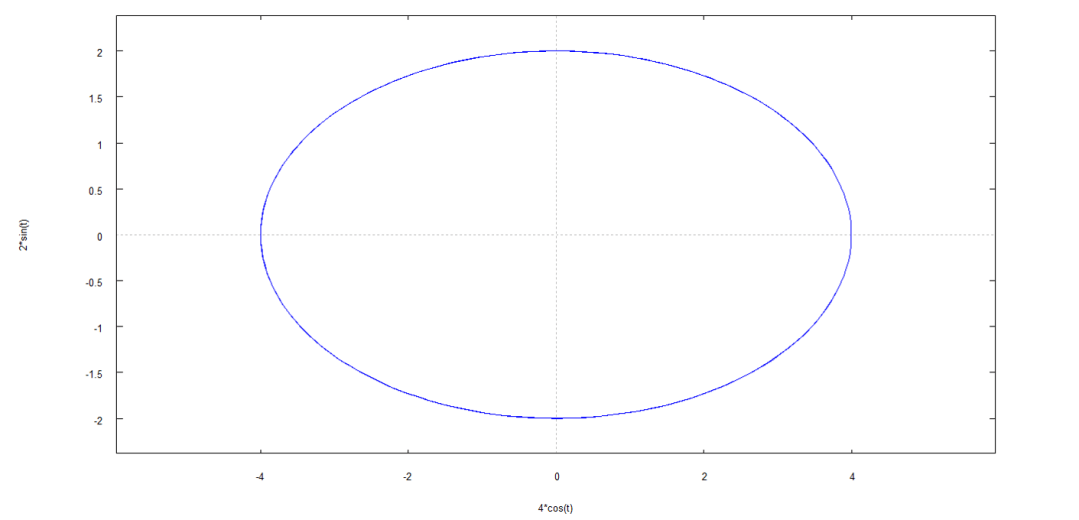
Imagen1 — *Figura 4.12.1 Trayectoria de las ecuaciones x_1=4 cos t y y_1=2 sen t.*

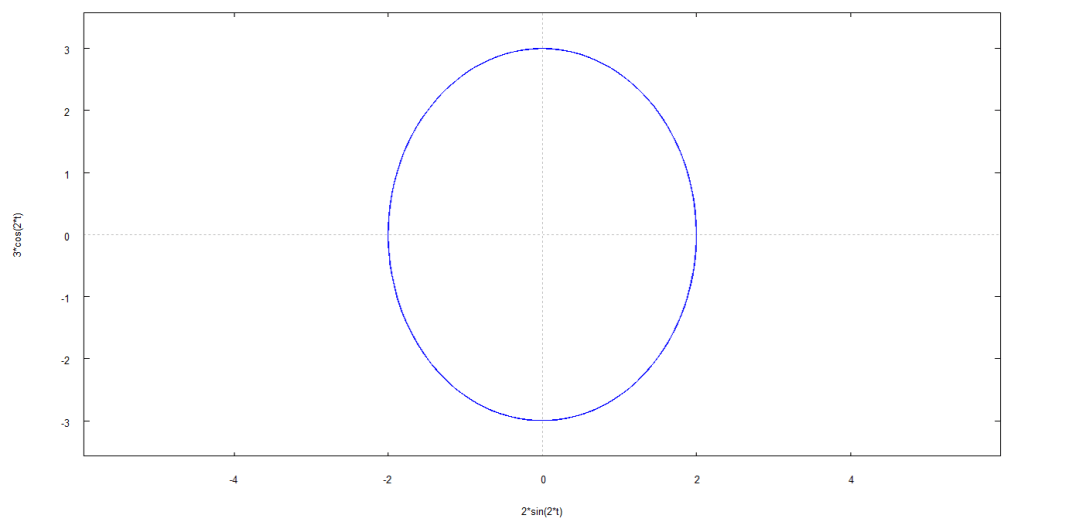
Imagen2 — *Figura 4.12.2 Trayectoria de las ecuaciones x_2=2 sen 2t y y_2=3 cos 2t.*

Imagen3 — *Figura 4.12.3 Trayectoria de las ecuaciones x_1=4 cos t, y_1=2 sen t, x_2=2 sen 2t y y_2=3 cos 2t.*

Regresando a la fórmula de la distancia

$\displaystyle s = \sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}}$

Derivándolo parcialmente con respecto a $x_1$

$\displaystyle \frac{ds}{dx_1} = \frac{\partial}{\partial x_1} (\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}})$

$\displaystyle \frac{ds}{dx_1} = \frac{1}{2\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}}} [-2(x_2-x_1)]$

$\displaystyle \frac{ds}{dx_1} = -\frac{(x_2-x_1)}{\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}}}$

Si $x_1=-4$ , $x_2=0$ , $y_1=0$ , $y_2=3$

$\displaystyle \frac{ds}{dx_1} = -\frac{(0+4)}{2\sqrt{{(0+4)}^{2} + {(3-0)}^{2}}} = -\frac{4}{\sqrt{16+9}} = -\frac{4}{\sqrt{25}}$

$\displaystyle \frac{ds}{dx_1} = -\frac{4}{5}$

Derivándolo parcialmente con respecto a $x_2$

$\displaystyle \frac{ds}{dx_2} = \frac{\partial}{\partial x_2} (\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}})$

$\displaystyle \frac{ds}{dx_2} = \frac{1}{2\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}}} [2(x_2-x_1)]$

$\displaystyle \frac{ds}{dx_2} = \frac{x_2-x_1}{\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}}}$

Si $x_1=-4$ , $x_2=0$ , $y_1=0$ , $y_2=3$

$\displaystyle \frac{ds}{dx_2} = \frac{0+4}{\sqrt{{(0+4)}^{2} + {(3-0)}^{2}}} = \frac{4}{\sqrt{16+9}} = \frac{4}{\sqrt{25}}$

$\displaystyle \frac{ds}{dx_2} = \frac{4}{5}$

Derivándolo parcialmente con respecto a $y_1$

$\displaystyle \frac{ds}{dy_1} = \frac{\partial}{\partial y_1} (\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}})$

$\displaystyle \frac{ds}{dy_1} = \frac{1}{2\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}}} [-2(y_2-y_1)]$

$\displaystyle \frac{ds}{dy_1} = -\frac{y_2-y_1}{\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}}}$

Si $x_1=-4$ , $x_2=0$ , $y_1=0$ , $y_2=3$

$\displaystyle \frac{ds}{dy_1} = -\frac{3-0}{2\sqrt{{(0+4)}^{2} + {(3-0)}^{2}}} = -\frac{3}{\sqrt{16+9}} = -\frac{3}{\sqrt{25}}$

$\displaystyle \frac{ds}{dy_1} = -\frac{3}{5}$

Derivándolo parcialmente con respecto a $y_2$

$\displaystyle \frac{ds}{dy_2} = \frac{\partial}{\partial y_2} (\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}} = \frac{1}{2\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}}} [2(y_2-y_1)]$

$\displaystyle \frac{ds}{dy_2} = \frac{y_2-y_1}{\sqrt{{(x_2-x_1)}^{2} + {(y_2-y_1)}^{2}}}$

Si $x_1=-4$ , $x_2=0$ , $y_1=0$ , $y_2=3$

$\displaystyle \frac{ds}{dy_2} = \frac{3-0}{\sqrt{{(0+4)}^{2} + {(3-0)}^{2}}} = \frac{3}{\sqrt{16+9}} = \frac{3}{\sqrt{25}}$

$\displaystyle \frac{ds}{dy_2} = \frac{3}{5}$

Ahora, derivando las cuatro funciones (es decir, $x_1$ , $x_2$ , $y_1$ y $y_2$ ) con respecto a “t”

$\displaystyle \frac{dx_1}{dt} = \frac{d}{dt} (4 \cos{t}) = 4 \frac{d}{dt} (\cos{t}) = -4 \sin{t}$

$\displaystyle \frac{dx_2}{dt} = \frac{d}{dt} (2 \sin{2t}) = 2 \frac{d}{dt} (\sin{2t}) = 2(2 \cos{2t}) = 4 \cos{2t}$

$\displaystyle \frac{dy_1}{dt} = \frac{d}{dt} (2 \sin{t}) = 2 \frac{d}{dt} (\sin{t}) = 2(\cos{t}) = 2 \cos{t}$

$\displaystyle \frac{dy_2}{dt} = \frac{d}{dt} (3 \cos{2t}) = 3 \frac{d}{dt} (\cos{2t}) = 3(-2 \sin{2t}) = -6 \sin{2t}$

Y reemplazando el valor de “t” en cada resultado de la derivada

$\displaystyle \frac{dx_1}{dt}{|}_{t=\pi} = -4 \sin{\pi} = -4(0) = 0$

$\displaystyle \frac{dx_2}{dt}{|}_{t=\pi} = 4 \cos{2\pi} = 4(1) = 4$

$\displaystyle \frac{dy_1}{dt}{|}_{t=\pi} = 2 \cos{\pi} = 2(-1) = -2$

$\displaystyle \frac{dy_2}{dt}{|}_{t=\pi} = -6 \sin{2\pi} = -6(0) = 0$

Regresando

$\displaystyle \frac{\partial s}{\partial t} = \frac{ds}{dx_1} \frac{dx_1}{dt} + \frac{ds}{dx_2} \frac{dx_2}{dt} + \frac{ds}{dy_1} \frac{dy_1}{dt} + \frac{ds}{dy_2} \frac{dy_2}{dt}$

Y sustituyendo con los valores obtenidos

$\displaystyle \frac{\partial s}{\partial t} = (-\frac{4}{5})(0) + (\frac{4}{5})(4) + (-\frac{3}{5})(-2) + (\frac{3}{5})(0)$

$\displaystyle \frac{\partial s}{\partial t} = 0 + \frac{16}{5} + \frac{6}{5} + 0 = \frac{22}{5}$

Por lo tanto

$\displaystyle \therefore \frac{\partial s}{\partial t} = \frac{22}{5}$

Referencias bibliográficas.

Colley, S. J. (2013). Cálculo vectorial. México: PEARSON EDUCACIÓN.
Larson, R., & Edwards, B. (2017). Matemáticas 3. Cálculo de varias variables. México: CENGAGE Learning.
R. Spiegel, M. (1967). Análisis vectorial. México: McGRAW – HILL.

Aplicación de la regla de la cadena a velocidades o ritmos de cambio relacionados. Cálculo vectorial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Aplicación de la regla de la cadena a velocidades o ritmos de cambio relacionados. Cálculo vectorial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta