Diferenciabilidad. Cálculo vectorial.

Introducción.

Una función f dada por $z = f(x,y)$ es diferenciable en $(x_0, y_0)$ si $\Delta z$ puede expresarse en la forma

$\Delta z = f_x (x_0, y_0)\Delta x + f_y (x_0, y_0) \Delta y + {\varepsilon}_1 \Delta x + {\varepsilon}_{2} \Delta y$

Donde ${\varepsilon}_{1}$ y ${\varepsilon}_{2} \rightarrow 0$ cuando $(\Delta x, \Delta y) \rightarrow (0,0)$ . La función es diferenciable a una región $\Re$ si es diferenciable en todo punto de $\Re$ .

Condición suficiente para la diferenciabilidad.

Si f es una función de x y y, para la que ${f}_{x}$ y ${f}_{y}$ son continuas en una región abierta $\Re$ , entonces f es diferenciable en $\Re$ .

Debe tenerse en cuenta que el término diferenciable se usa de manera diferente para funciones de dos variables y para funciones de una variable. Una función de una variable es diferenciable en un punto si su derivada existe en el punto. Sin embargo, en el caso de una función de dos variables, la existencia de las derivadas parciales $f_x$ y $f_y$ no garantiza que la función sea diferenciable.

Diferenciabilidad que implica continuidad.

Si una función de “x” y “y” es diferenciable en $(x_0,y_0)$ , entonces es continua en $(x_0,y_0)$ .

Problemas resueltos.

Problema 1. Mostrar que una función es diferenciable para

$f(x,y) = x^2 + 3y$

Solución. Se calcula el incremento $\Delta z$

$\Delta z = f(x + \Delta x, y + \Delta y) - f(x, y)$

$\Delta z = [{(x+\Delta x)}^{2} + 3(y+\Delta y)] - (x^2 + 3y)$

$\Delta z =x^2 + 2x \Delta x + {(\Delta x)}^{2} + 3y + 3\Delta y - x^2 - 3y$

$\Delta z = 2x\Delta x + {(\Delta x)}^{2} + 3\Delta y$

Ahora, con esta expresión

$\Delta z = 2x \Delta x + {(\Delta x)}^{2} + 3\Delta y$

Recordando la fórmula

$\Delta z = f_x (x_0, y_0)\Delta x + f_y (x_0, y_0)\Delta y + {\varepsilon}_{1} \Delta x + {\varepsilon}_{2} \Delta y$

Y comparando

$\Delta z = (2x)\Delta x + (3)\Delta y + (\Delta x)\Delta x+ (0)\Delta y$

Se concluye que ${\varepsilon}_{1} = \Delta x$ y ${\varepsilon}_{2} = 0$ . Si ${\varepsilon}_{1} \rightarrow 0$ y ${\varepsilon}_{2} \rightarrow 0$ cuando $(\Delta x, \Delta y) \rightarrow (0, 0)$ , se dice que f es diferenciable en todo punto en el plano.

Problema 2. Demostrar que $f_x (0,0)$ y $f_y (0,0)$ existen, pero f no es diferenciable en (0,0), donde f está definida como

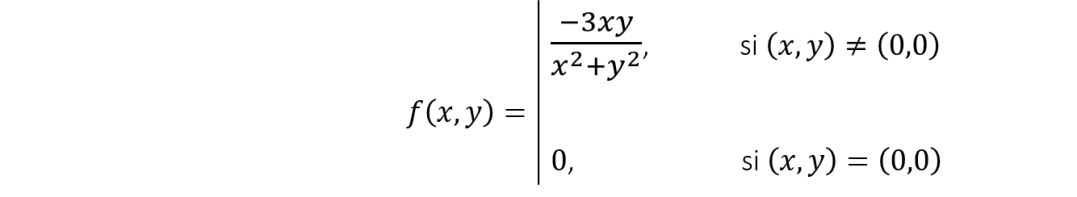
Imagen1

Solución. Para demostrar esto, basta con mostrar que f no es continua en el punto (0,0). Se observa en la gráfica los valores de $f(x,y)$ a lo largo de dos trayectorias diferentes que se aproximan a (0,0).

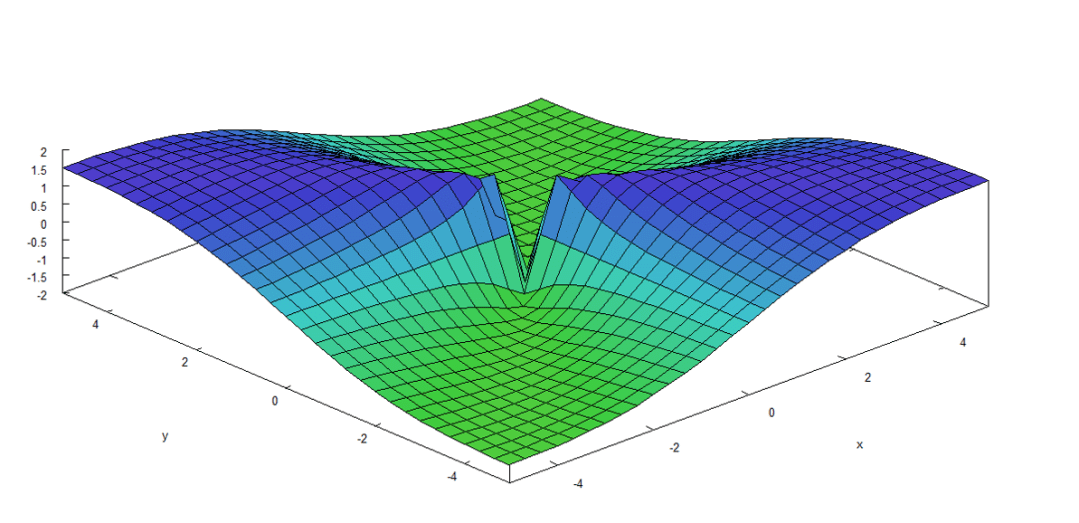
Imagen2

A lo largo de la recta $y=x$ , el límite es

$\displaystyle \lim_{(x,x) \rightarrow (0,0)}{f(x,y)} = \lim_{(x,x) \rightarrow (0,0)}{[\frac{-3x(x)}{x^2+(x)^2}]} = \lim_{(x,x) \rightarrow (0,0)}{(\frac{-3x^2}{x^2+x^2})}$

$\displaystyle = \lim_{(x,x) \rightarrow (0,0)}{(-\frac{3x^2}{2x^2})} = \lim_{(x,x) \rightarrow (0,0)}{(-\frac{3}{2})} = -\frac{3}{2}$

Esto se interpreta que a lo largo de la recta $y=x$ , $f(x,y)$ se aproxima o tiende a $\displaystyle -\frac{3}{2}$ .

Mientras que a lo largo de $y=-x$ se tiene que

$\displaystyle \lim_{(x,-x) \rightarrow (0,0)}{f(x,y)} = \lim_{(x,-x) \rightarrow (0,0)}{[\frac{-3x(-x)}{x^2+(-x)^2}]} = \lim_{(x,-x) \rightarrow (0,0)}{(\frac{3x^2}{x^2+x^2})}$

$\displaystyle = \lim_{(x,-x) \rightarrow (0,0)}{(\frac{3x^2}{2x^2})} = \lim_{(x,-x) \rightarrow (0,0)}{(\frac{3}{2})} = \frac{3}{2}$

Esto se interpreta que a lo largo de la recta $y=-x$ , $f(x,y)$ se aproxima o tiende a $\displaystyle \frac{3}{2}$ .

Por lo que el límite de f(x,y) cuando $(x,y) \rightarrow (0,0)$ no existe, y se concluye que f no es continua en (0,0). Por lo tanto, f no es diferenciable en (0,0). Por otro lado, de la función f(x,y), sus derivadas parciales son

$\displaystyle {f}_{x} (0,0) = \lim_{\Delta x \rightarrow 0}{[\frac{f(\Delta x,0) - f(0,0)}{\Delta x}]}$

$\displaystyle {f}_{x} (0,0) = \lim_{\Delta x \rightarrow 0}{[\frac{-\frac{3{(\Delta x)}^{2} (0)}{{(\Delta x)}^{2} + {0}^{2}} - (-\frac{3(0)(0)}{0^2+0^2})}{\Delta x}]} = \lim_{\Delta x \rightarrow 0}{(\frac{-0+0}{\Delta x})}$

$f_x (0,0)=0$

$\displaystyle f_y (0,0) = \lim_{\Delta y \rightarrow 0}{[\frac{f(0,\Delta y) - f(0,0)}{\Delta y}]}$

$\displaystyle {f}_{y} (0,0) = \lim_{\Delta y \rightarrow 0}{[\frac{-\frac{3{(0)}^{2} (\Delta y)}{0^2 + {(\Delta y)}^{2}}) -(-\frac{3(0)(0)}{0^2+0^2})}{\Delta y}]} = \lim_{\Delta y \rightarrow 0}{(\frac{-0+0}{\Delta y})}$

$f_y (0,0)=0$

Por lo que, las derivadas parciales en (0,0) existen.

Referencias bibliográficas.

Colley, S. J. (2013). Cálculo vectorial. México: PEARSON EDUCACIÓN.
Larson, R., & Edwards, B. (2017). Matemáticas 3. Cálculo de varias variables. México: CENGAGE Learning.
R. Spiegel, M. (1967). Análisis vectorial. México: McGRAW – HILL.

Diferenciabilidad. Cálculo vectorial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Diferenciabilidad. Cálculo vectorial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta