Coordenadas cilíndricas y coordenadas esféricas. Cálculo vectorial.

Sistema de coordenadas cilíndricas.

En un sistema de coordenadas cilíndricas, un punto P en el espacio se representa por medio de una terna ordenada $(r, \theta, z)$ .

$(r, \theta)$ es la representación polar de la proyección de P en el plano xy.
z es distancia de $(r, \theta)$ a P.

Imagen1 — *Figura 4.14.1 Representación gráfica del sistema de coordenadas cilíndricas.*

Conversiones cilíndricas y rectangulares.

Conversión de coordenadas cilíndricas a rectangulares

$x = r \cos{\theta}$

$y = r \sin{\theta}$

$z=z$

Conversión de coordenadas rectangulares a cilíndricas

$r^2=x^2+y^2$

$\displaystyle \tan{\theta} = \frac{y}{x}$

$z=z$

Problemas resueltos.

Problema 1. Convertir el punto $\displaystyle (r,\theta,z) = (4, \frac{5\pi}{6},3)$ a coordenadas rectangulares.

Solución. Se llevará a cabo la conversión de coordenadas cilíndricas a rectangulares. Para ello, se sabe que, $r=4$ , $\displaystyle \frac{5\pi}{6}$ y $z=3$ , entonces, utilizando las fórmulas y sustituyendo

$x = r \cos{\theta}$

$\displaystyle x = 4 \cos{\frac{5\pi}{6}} = 4(-\frac{\sqrt{3}}{2})$

$\displaystyle x = -2\sqrt{3}$

___

$y = r \sin{\theta}$

$\displaystyle y = 4 \sin{\frac{5\pi}{6}} = 4 (\frac{1}{2})$

$y=2$

___

$z=z$

$z=3$

Finalmente, las coordenadas rectangulares son $\displaystyle (-2\sqrt{3}, 2, 3)$

Problema 2. Convertir el punto $\displaystyle (x,y,z) = (1,\sqrt{3},2)$ a coordenadas cilíndricas.

Solución. Se llevará a cabo la conversión de coordenadas rectangulares a cilíndricas. Para ello, se sabe que, $x=1$ , $\displaystyle y=\sqrt{3}$ y $z=2$ , entonces, utilizando las fórmulas y sustituyendo

$r^2 = x^2 + y^2$

$\displaystyle r = \sqrt{x^2+y^2}$

$\displaystyle r = \sqrt{{(1)}^{2} + {(\sqrt{3})}^{2}}$

$\displaystyle r = \sqrt{1+3} = \sqrt{4}$

$r=2$

___

$\displaystyle \tan{\theta} = \frac{y}{x}$

$\theta = \arctan{(\frac{y}{x})}$

$\displaystyle \theta = \arctan{(\frac{\sqrt{3}}{1})}$

$\displaystyle \theta = \arctan{(\sqrt{3})}$

$\displaystyle \theta = \frac{\pi}{3}$

___

$z=z$

$z=2$

Finalmente, las coordenadas cilíndricas son $\displaystyle (2,\frac{\pi}{3},2)$

Problema 3. Hallar una ecuación en coordenadas cilíndricas para la superficie representada por cada ecuación rectangular.

a) $x^2+y^2=4z^2$

b) $y^2=x$

Solución a). Utilizando las fórmulas para convertir de coordenadas rectangulares a cilíndricas: $\displaystyle r^2 = x^2 + y^2$ , $\displaystyle \tan{\theta} = \frac{y}{x}$ , $z=z$ .

Se observa que

$x^2+y^2=4z^2$

$r^2=4z^2$

Y este es la ecuación representada en coordenadas cilíndricas.

Imagen2 — *Figura 4.14.2 Representación gráfica de la ecuación rectangular x^2+y^2=4z^2.*

Solución b). Utilizando las fórmulas para convertir de coordenadas rectangulares a cilíndricas y viceversa: $r^2=x^2+y^2$ , $y=r \sin{\theta}$ , $x = r \cos{\theta}$ , $\displaystyle \tan{\theta} = \frac{y}{x}$ , $z=z$ .

Se observa que

$y^2=x$

${(r \sin{\theta})}^{2} = r \cos{\theta}$

$r^2 {\sin}^{2}{\theta} = r \cos{\theta}$

$r {\sin}^{2}{\theta} = \cos{\theta}$

$\displaystyle r = \frac{\cos{\theta}}{{\sin}^{2}{\theta}} = \csc{\theta} \cot{\theta}$

Y esta es la ecuación representada en coordenadas cilíndricas.

Imagen3 — *Figura 4.14.3 Representación gráfica de la ecuación rectangular y^2=x.*

Problema 4. Hallar una ecuación en coordenadas rectangulares de la superficie representada por la ecuación cilíndrica $r^2 \cos{2\theta} + z^2 + 1 = 0$ .

Solución. Utilizando las fórmulas para convertir de coordenadas cilíndricas a rectangulares: $x=r \cos{\theta}$ , $y=r \sin{\theta}$ , $z=z$

Se observa que

$r^2 \cos{2\theta} + z^2 + 1 = 0$

$r^2 ({\cos}^{2}{\theta} - {\sin}^{2}{\theta}) + z^2 + 1 = 0$

$r^2 {\cos}^{2}{\theta} - r^2 {\sin}^{2}{\theta} + z^2 + 1 = 0$

${(r \cos{\theta})}^{2} - {(r \sin{\theta})}^{2} + z^2 + 1 = 0$

${(x)}^{2} - {(y)}^{2} + z^2 + 1 = 0$

$x^2 - y^2 + z^2 + 1 = 0$

$y^2 - x^2 - z^2 = 1$

Y esta es la ecuación representada en coordenadas rectangulares.

Imagen4 — *Figura 4.14.4 Representación gráfica de la ecuación cilíndrica r^2 cos⁡2θ+z^2+1=0.*

El sistema de coordenadas esféricas es útil cuando las superficies en el espacio presentan un punto o centro de simetría. A continuación, se presentan tres superficies con sus respectivas ecuaciones esféricas básicas.

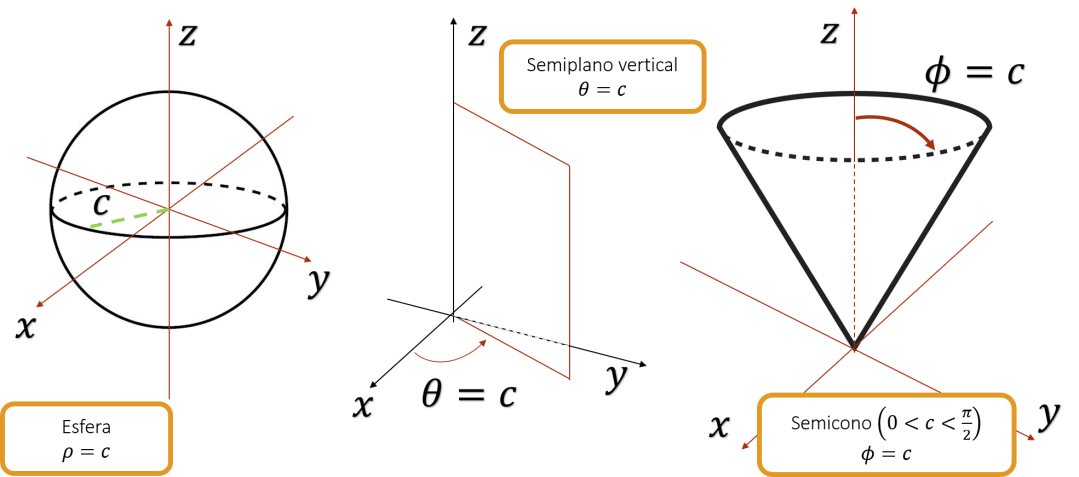
Imagen5 — *Figura 4.14.5 Representación gráfica de las superficies en el espacio representadas en ecuaciones esféricas.*

Sistema de coordenadas esféricas.

En un sistema de coordenadas esféricas, un punto P en el espacio se representa por medio de una terna ordenada $(\rho, \theta, \phi)$ .

$\rho$ es la distancia entre P y el origen, $\rho \ge 0$ .
$\theta$ es el mismo ángulo utilizado en coordenadas cilíndricas para $r \ge 0$ .
$\phi$ es el ángulo entre el eje z positivo y el segmento de recta $\rho$ , $0 \le \phi \le \pi$ .

Se debe observar que $\rho$ y $\phi$ son no negativas.

Imagen6 — *Figura 4.14.6 Representación gráfica del sistema de coordenadas esféricas.*

Conversiones rectangulares y esféricas.

Conversión de coordenadas esféricas a rectangulares

$x = \rho \sin{\phi} \cos{\theta}$

$y = \rho \sin{\phi} \sin{\theta}$

$z = \rho \cos{\phi}$

Conversión de coordenadas rectangulares a esféricas

${\rho}^{2} = x^2+y^2+z^2$

$\displaystyle \tan{\theta} = \frac{y}{x}$

$\displaystyle \phi = {\cos}^{-1}{(\frac{z}{\sqrt{x^2+y^2+z^2}})}$

Conversiones cilíndricas y esféricas.

Conversión de coordenadas esféricas a cilíndricas $(r \ge 0)$

$r^2 = {\rho}^{2} \sin{\phi}$

$\theta = \theta$

$z = \rho \cos{\phi}$

Conversión de coordenadas cilíndricas a esféricas $(r \ge 0)$

$\displaystyle \rho = \sqrt{r^2+z^2}$

$\theta = \theta$

$\displaystyle \phi = {cos}^{-1}{(\frac{z}{\sqrt{r^2+z^2}})}$

Problemas resueltos.

Problema 5. Hallar una ecuación en coordenadas esféricas para la superficie representada por cada una de la ecuaciones rectangulares.

a) Cono: $x^2+y^2=z^2$

b) Esfera: $x^2+y^2+z^2-4z=0$

Solución a). Utilizando las fórmulas para convertir de coordenadas rectangulares a esféricas y viceversa: $\rho^2 = x^2 + y^2 + z^2$ . $\displaystyle \tan{\theta} = \frac{y}{x}$ , $\rho = {\cos}^{-1}{(\frac{z}{\sqrt{x^2+y^2+z^2}})}$ , $x = \rho \sin{\phi} \cos{\theta}$ , $y = \rho \sin{\phi} \sin{\theta}$ , $z = \rho \cos{\phi}$ .

Se observa que

$x^2+y^2=z^2$

${(\rho \sin{\phi} \cos{\theta})}^{2} + {(\rho \sin{\phi} \sin{\theta})}^{2} = {(\rho \cos{\phi})}^{2}$

$\rho^2 {\sin}^{2}{\phi} {\cos}^{2}{\theta} + {\rho}^{2} {\sin}^{2}{\phi} {\sin}^{2}{\theta} = {\rho}^{2} {\cos}^{2}{\phi}$

${\rho}^{2} {\sin}^{2}{\phi} ({\cos}^{2}{\theta} + {\sin}^{2}{\theta}) = {\rho}^{2} {\cos}^{2}{\phi}$

Recordando que ${\cos}^{2}{\theta} + {\sin}^{2}{\theta} = 1$

${\rho}^{2} {\sin}^{2}{\phi} (1) = {\rho}^{2} {\cos}^{2}{\phi}$

Si $\rho \ge 0$

${\sin}^{2}{\phi} = {\cos}^{2}{\phi}$

$\displaystyle \frac{{\sin}^{2}{\phi}}{{\cos}^{2}{\phi}} = 1$

${\tan}^{2}{\phi} = 1$

$\tan{\phi} = 1$

$\phi = \arctan{(1)} = \frac{1}{4} \pi = \frac{3\pi}{4}$

Y esta es la ecuación representada en coordenadas esféricas, la cual, $\displaystyle \phi = \frac{1}{4} \pi$ es un semicono superior, y $\displaystyle \phi = \frac{3}{4} \pi$ es un semicono inferior.

Imagen7 — *Figura 4.14.7 Representación gráfica de la ecuación rectangular x^2+y^2=z^2.*

Solución b). Utilizando las fórmulas para convertir de coordenadas rectangulares a esféricas y viceversa: ${\rho}^{2} = x^2 + y^2 + z^2$ . $\displaystyle \tan{\theta} = \frac{y}{x}$ , $\phi = {cos}^{-1}{(\frac{z}{\sqrt{x^2+y^2+z^2}})}$ , $x=\rho \sin{\phi} \cos{\theta}$ , $y=\rho \sin{\phi} \sin{\theta}$ , $z= \rho \cos{\phi}$ .

Se observa que

$x^2+y^2+z^2-4z=0$

${(\rho \sin{\phi} \cos{\theta})}^{2} + {(\rho \sin{\phi} \sin{\theta})}^{2} + {(\rho \cos{\phi})}^{2} - 4(\rho \cos{\phi}) = 0$

${\rho}^{2} {\sin}^{2}{\phi} {\cos}^{2}{\theta} + {\rho}^{2} {\sin}^{2}{\phi} {\sin}^{2}{\theta} + {\rho}^{2} {\cos}^{2}{\phi} - 4\rho \cos{\phi} = 0$

${\rho}^{2} {\sin}^{2}{\phi}({\cos}^{2}{\theta} + {\sin}^{2}{\theta}) + {\rho}^{2} {\cos}^{2}{\phi} - 4\rho \cos{\phi} = 0$

${\rho}^{2} {\sin}^{2}{\phi}(1) + {\rho}^{2} {\cos}^{2}{\phi} - 4\rho \cos{\phi} = 0$

${\rho}^{2} {\sin}^{2}{\phi} + {\rho}^{2} {\cos}^{2}{\phi} - 4\rho \cos{\phi} = 0$

${\rho}^{2} ({\sin}^{2}{\phi} + {\cos}^{2}{\phi}) - 4\rho \cos{\phi} = 0$

${\rho}^{2} (1) - 4\rho \cos{\phi} = 0$

${\rho}^{2} - 4\rho \cos{\phi} = 0$

${\rho}^{2} = 4\rho \cos{\phi}$

$\rho = 4 \cos{\phi}$

Y esta es la ecuación representada en coordenadas esféricas.

Imagen8 — *Figura 4.14.8 Representación gráfica de la ecuación rectangular x^2+y^2+z^2-4z=0.*

Referencias bibliográficas.

Colley, S. J. (2013). Cálculo vectorial. México: PEARSON EDUCACIÓN.
Larson, R., & Edwards, B. (2017). Matemáticas 3. Cálculo de varias variables. México: CENGAGE Learning.
R. Spiegel, M. (1967). Análisis vectorial. México: McGRAW – HILL.

Coordenadas cilíndricas y coordenadas esféricas. Cálculo vectorial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Coordenadas cilíndricas y coordenadas esféricas. Cálculo vectorial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta