Método de bisección. Segundo método cerrado. Métodos numéricos.

Introducción

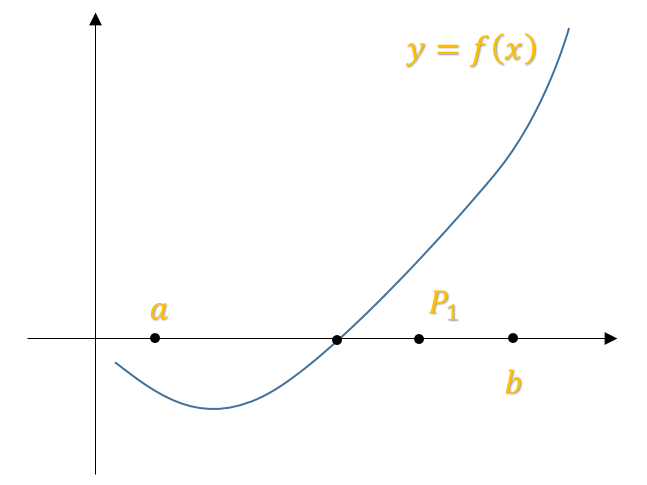
Dada una función $y=f(x)$ graficada en el plano $xy$ , se toma arbitrariamente los límites inferior y superior sobre el eje $x$ y formará un intervalo cerrado. Dentro de ese intervalo, la función deberá intersectar sobre el eje $x$ , ya que esto representa el cambio de signo (raíz) y el valor numérico de $x$ .

Imagen1 — *Figura 1. Representación gráfica de una función.*

El método de bisección consiste en calcular el parámetro $P$ tantas veces como sea posible (comparando con los valores de cada error) formando subintervalos cerrados. Cuando se considere que el último valor de $P$ sea el adecuado, automáticamente, representará el valor de $x$ donde la función presenta ese cambio de signo.

En general, para calcular la variable $P$

$\displaystyle P_n = \frac{a_n + b_n }{2}$

En cada subintervalo, para obtener $P_1$

$\displaystyle [a_1 , b_1 ] = [a, b] \rightarrow P_1 = \frac{a+b}{2}$

Para obtener $P_2$

$\displaystyle [a_2 , b_2 ] = [a_1 , P_1 ] \rightarrow P_2 = \frac{a_1 + P_1 }{2}$

Para obtener $P_3$

$\displaystyle [a_3 , b_3 ] = [P_1 , P_2 ] \rightarrow P_3 = \frac{P_1 + P_2}{2}$

La secuencia de subintervalos es la siguiente

$[a, b] \rightarrow [a, P_1 ] \rightarrow [P_1 , P_2 ] \rightarrow [ \cdots , \cdots ] \rightarrow [P_{n-1} , P_n ]$

Y para calcular el error

$E_n = |P_n - P_{n-1} |$

Problemas resueltos

Problema 1. Encontrar la raíz positiva de $x^3 + 4x^2 - 16 = 0$ con tolerancia de $0.02$

Solución. Se realiza una tabulación usando solo valores del dominio positivos desde $x=0$ hasta $x=2$ .

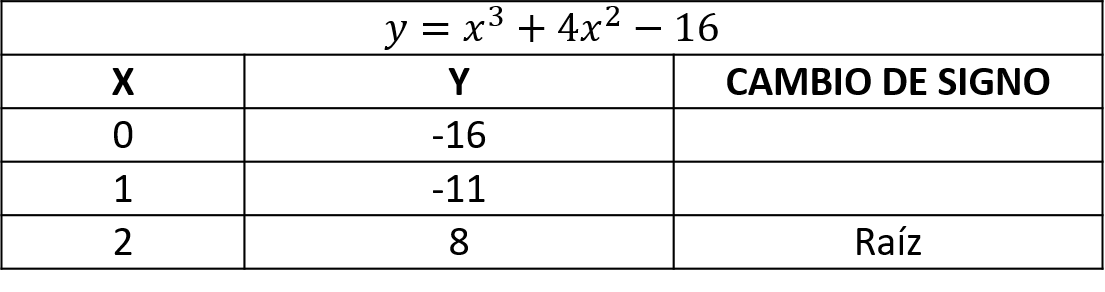
En la tabulación, la función presenta un cambio de signo entre $x =1$ y $x=2$ , por lo que el intervalo a tomar es $[1,2]$ . Luego, los valores a utilizar son $a=1$ y $b=2$ .

$[1, 2] \rightarrow a=1$ y $b=2$

De la función brindada por el problema, se evalúan los valores para $a=1$ y $b=2$ .

$f(x) = x^3 + 4x^2 - 16$

En la primera iteración, con el intervalo $[1,2]$ , calculando $P_1$

$\displaystyle P_1 = \frac{a_1 + b_1}{2} = \frac{a+b}{2}$

$\displaystyle P_1 = \frac{1+2}{2} = \frac{3}{2}$

$P_1 = 1.5$

El valor de $P_1$ será evaluado en la función $f(x)$

$f(x) = x^3 + 4x^2 - 16$

$f(P_1 ) = f(1.5) = (1.5)^3 + 4(1.5)^2 - 16$

$f(1.5) = -3.635$

Este resultado tiene un signo negativo, para obtener el siguiente intervalo, el valor de $a$ o $b$ será remplazado por el valor de $P_1$ . Para identificarlo, se observa que el valor de $P_1$ , al evaluarlo, se tiene un resultado con signo negativo, por lo que, los valores de $a$ y de $b$ (del intervalo $[1,2]$ ) al momento de evaluarlos en la función $f(x)$ , debe de mostrarse el mismo signo con lo que se obtuvo $f(P_1 )$ , y el indicado es el valor de $a=1$ (ya que muestra un resultado con signo negativo). Por lo que, del primer intervalo

$[a_1, b_1 ] = [a,b] = [1,2]$

El segundo intervalo es

$[a_2, b_2 ] = [P_1 , b] = [1.5,2]$

De la función brindada por el problema, se evalúan los valores para $P_1 = 1.5$ y $b=2$ .

$f(x) = x^3 + 4x^2 - 16$

En la segunda iteración, con el intervalo $[1.5 , 2]$ , calculando $P_2$

$\displaystyle P_2 = \frac{a_2 + b_2}{2} = \frac{P_1 + b}{2}$

$\displaystyle P_2 = \frac{1.5+2}{2} = \frac{3.5}{2}$

$P_2 = 1.75$

El valor de $P_2$ será evaluado en la función $f(x)$

$f(x) = x^3 + 4x^2 - 16$

f(P_2 ) = f(1.75) = (1.75)^3 + 4(1.75)^2 - 16

Este resultado tiene un signo positivo, para obtener el siguiente intervalo, el valor de $P_1$ o $b$ será remplazado por el valor de $P_2$ . Para identificarlo, se observa que el valor de $P_2$ , al evaluarlo, se tiene un resultado con signo positivo, por lo que, los valores de $P_1$ y de $b$ (del intervalo $[1.5, 2]$ ) al momento de evaluarlos en la función $f(x)$ , debe de mostrarse el mismo signo con lo que se obtuvo $f(P_2 )$ , y el indicado es el valor de $b=2$ (ya que muestra un resultado con signo positivo). Por lo que, del segundo intervalo

$[a_2, b_2 ] = [P_1 , b] = [1.5, 2]$

El tercer intervalo es

$[a_3 , b_3 ] = [P_1 , P_2 ] = [1.5, 1.75]$

Calculando el valor del primer error

$E_1 = |P_2 - P_1 |$

$E_1 = |1.75 - 1.5| = |0.25|$

$E_1 = 0.25$

Comparando con el valor de $E_1$ con el valor de la tolerancia

$0.25 > 0.02$

Se observa que el valor del primer error es mayor que la tolerancia, por lo que se pasa a la siguiente iteración.

De la función brindada por el problema, se evalúan los valores para $P_1 = 1.5$ y $P_2 = 1.75$ .

$f(x) = x^3 + 4x^2 - 16$

En la tercera iteración, con el intervalo $[1.5,1.75]$ , calculando $P_3$

$\displaystyle P_3 = \frac{a_3 + b_3}{2} = \frac{P_1 + P_2}{2}$

$\displaystyle P_3 = \frac{1.5+1.75}{2} = \frac{3.25}{2}$

$P_3 = 1.625$

El valor de $P_3$ será evaluado en la función $f(x)$

$f(x) = x^3 + 4x^2 - 16$

f(P_3 ) = f(1.625) = (1.625)^3 + 4(1.625)^2 - 16

Este resultado tiene un signo negativo, para obtener el siguiente intervalo, el valor de $P_1$ o $P_2$ será remplazado por el valor de $P_3$ . Para identificarlo, se observa que el valor de $P_3$ , al evaluarlo, se tiene un resultado con signo negativo, por lo que, los valores de $P_1$ y de $P_2$ (del intervalo $[1.5, 1.75]$ ) al momento de evaluarlos en la función $f(x)$ , debe de mostrarse el mismo signo con lo que se obtuvo $f(P_3 )$ , y el indicado es el valor de $P_1 = 1.5$ (ya que muestra un resultado con signo negativo). Por lo que, del tercer intervalo

$[a_3 , b_3 ] = [P_1 , P_2 ] = [1.5, 1.75]$

El cuarto intervalo es

$[a_4 , b_4 ] = [P_3 , P_2 ] = [1.625 , 1.75]$

Calculando el valor del segundo error

$E_2 = |P_3 - P_2 |$

$E_2 = |1.625-1.75|= |-0.125|$

$E_2 = 0.125$

Comparando con el valor de $E_2$ con el valor de la tolerancia

$0.125 > 0.02$

Se observa que el valor del segundo error es mayor que la tolerancia, por lo que se pasa a la siguiente iteración.

De la función brindada por el problema, se evalúan los valores para $P_3 = 1.625$ y $P_2 = 1.75$ .

$f(x) = x^3 + 4x^2 - 16$

En la cuarta iteración, con el intervalo $[1.625,1.75]$ , calculando $P_4$

$\displaystyle P_4 = \frac{a_4 + b_4}{2}$

$\displaystyle P_4 = \frac{1.625+1.75}{2} = \frac{3.375}{2}$

$P_4 = 1.688$

El valor de $P_4$ será evaluado en la función $f(x)$

$f(x) = x^3 + 4x^2 - 16$

f(P_4 ) = f(1.688) = (1.688)^3 + 4(1.688)^2 - 16

Este resultado tiene un signo positivo, para obtener el siguiente intervalo, el valor de $P_3$ o $P_2$ será remplazado por el valor de $P_4$ . Para identificarlo, se observa que el valor de $P_4$ , al evaluarlo, se tiene un resultado con signo positivo, por lo que, los valores de $P_3$ y de $P_2$ (del intervalo $[1.625, 1.75]$ ) al momento de evaluarlos en la función $f(x)$ , debe de mostrarse el mismo signo con lo que se obtuvo $f(P_4 )$ , y el indicado es el valor de $P_2 = 1.75$ (ya que muestra un resultado con signo positivo). Por lo que, del cuarto intervalo

$[a_4 , b_4 ] = [P_3 , P_2 ] = [1.625, 1.75]$

El quinto intervalo es

$[a_5 , b_5 ] = [P_3 , P_4 ] = [1.625 , 1.688]$

Calculando el valor del tercer error

$E_3 = |P_4 - P_3 |$

$E_3 = |1.688 - 1.625|= |0.063|$

$E_3 = 0.063$

Comparando con el valor de $E_3$ con el valor de la tolerancia

$0.063 > 0.02$

Se observa que el valor del tercer error es mayor que la tolerancia, por lo que se pasa a la siguiente iteración.

De la función brindada por el problema, se evalúan los valores para $P_3 = 1.625$ y $P_4 = 1.688$ .

$f(x) = x^3 + 4x^2 - 16$

En la quinta iteración, con el intervalo $[1.625,1.688]$ , calculando $P_5$

$\displaystyle P_5 = \frac{a_5 + b_5}{2} = \frac{P_3 + P_4}{2}$

$\displaystyle P_5 = \frac{1.625 + 1.688}{2} = \frac{3.313}{2}$

$P_5 = 1.657$

El valor de $P_5$ será evaluado en la función $f(x)$

$f(x) = x^3 + 4x^2 - 16$

f(P_5 ) = f(1.657) = (1.657)^3 + 4(1.657)^2 - 16

Este resultado tiene un signo negativo, para obtener el siguiente intervalo, el valor de $P_3$ o $P_4$ será remplazado por el valor de $P_5$ . Para identificarlo, se observa que el valor de $P_5$ , al evaluarlo, se tiene un resultado con signo negativo, por lo que, los valores de $P_3$ y de $P_4$ (del intervalo $[1.625, 1.688]$ ) al momento de evaluarlos en la función $f(x)$ , debe de mostrarse el mismo signo con lo que se obtuvo $f(P_5 )$ , y el indicado es el valor de $P_3 = 1.625$ (ya que muestra un resultado con signo negativo). Por lo que, del cuarto intervalo

$[a_4 , b_4 ] = [P_3 , P_4 ] = [1.625 , 1.688]$

El quinto intervalo es

$[a_5 , b_5 ] = [P_5 , P_4 ] = [1.657 , 1.688]$

Calculando el valor del cuarto error

$E_4 = |P_5 - P_4 |$

$E_4 = |1.657 - 1.688| = |0.031|$

$E_4 = 0.031$

Comparando con el valor de $E_4$ con el valor de la tolerancia

$0.031 > 0.02$

Se observa que el valor del cuarto error es mayor que la tolerancia, por lo que se pasa a la siguiente iteración.

De la función brindada por el problema, se evalúan los valores para $P_5=1.657$ y $P_4 = 1.688$ .

$f(x) = x^3 + 4x^2 - 16$

En la sexta iteración, con el intervalo $[1.657,1.688]$ , calculando $P_6$

$\displaystyle P_6 = \frac{a_6 + b_6}{2} = \frac{P_5 + P_4}{2}$

$\displaystyle P_6 = \frac{1.657+1.688}{2} = \frac{3.313}{2}$

$P_6 = 1.673$

El valor de $P_6$ será evaluado en la función $f(x)$

$f(x) = x^3 + 4x^2 - 16$

f(P_6 ) = f(1.673) = (1.673)^3 + 4(1.673)^2 - 16

Este resultado tiene un signo negativo, para obtener el siguiente intervalo, el valor de $P_5$ o $P_4$ será remplazado por el valor de $P_6$ . Para identificarlo, se observa que el valor de $P_6$ , al evaluarlo, se tiene un resultado con signo negativo, por lo que, los valores de $P_5$ y de $P_4$ (del intervalo $[1.657, 1.688]$ ) al momento de evaluarlos en la función $f(x)$ , debe de mostrarse el mismo signo con lo que se obtuvo $f(P_6 )$ , y el indicado es el valor de $P_5 = 1.657$ (ya que muestra un resultado con signo negativo). Por lo que, del sexto intervalo

$[a_5 , b_5 ] = [P_5 , P_4 ] = [1.657 , 1.688]$

El sexto intervalo es

$[a_6 , b_6 ] = [P_6 , P_4 ] = [1.657 , 1.673]$

Calculando el valor del quinto error

$E_5 = |P_6 - P_5 |$

$E_5 = |1.673 - 1.657| = |0.016|$

$E_5 = 0.016$

Comparando con el valor de $E_5$ con el valor de la tolerancia

$0.016 < 0.02$

Se observa que el valor del quinto error ya es menor que la tolerancia, por lo que, el último valor calculado (es decir, $P_6 = 1.673$ ) es el valor indicado. Finalmente

$\therefore x = 1.673$

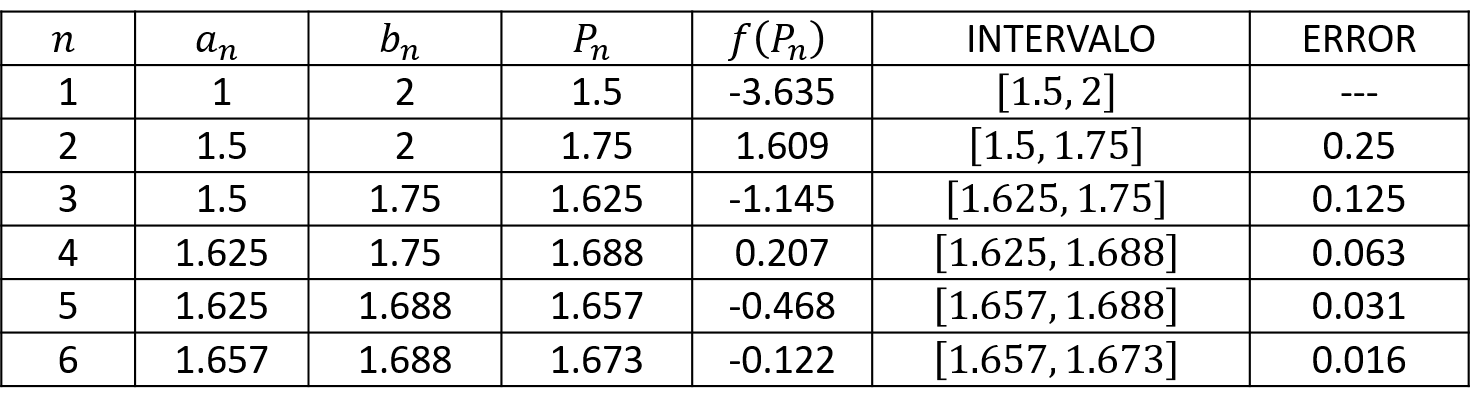
A continuación, se muestra una tabla referente a todos los valores calculados por el método de bisección.

Método de bisección. Segundo método cerrado. Métodos numéricos.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Método de bisección. Segundo método cerrado. Métodos numéricos.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta