Solución de un sistema de ecuaciones no lineales por el método del punto fijo. Métodos numéricos.

Introducción

Sean las funciones

De la ecuación (A), se despeja $x$ y de la ecuación (B), se despeja $y$

A partir de esto, para más iteraciones (es decir, para n=0, 1, 2, 3, …)

Los puntos lineales son $(x_0,y_0 )$ .

Criterio de convergencia

Sean $F_x$ y $F_y$ las derivadas parciales de $F(x,y)$ , entonces, el criterio de convergencia consiste de la siguiente manera

$|F_x |+|F_y | < 1$

$\displaystyle |\frac{\partial F}{\partial x} |+|\frac{\partial F}{\partial y}| < 1$

Y para la función $G(x,y)$ , también puede utilizarse el criterio de convergencia

$|G_x |+|G_y | < 1$

$\displaystyle \left|\frac{\partial G}{\partial x} \right|+ \left|\frac{\partial G}{\partial y} \right| < 1$

Esto se refiere que, si las derivadas parciales de $F(x,y)$ y $G(x,y)$ cumplen con la condición del criterio de convergencia, el sistema de ecuaciones no lineales tiene solución única, además de que las ecuaciones (A) y B) son las adecuadas.

Para calcular el error, su fórmula es la siguiente

$E_{n+1} = \max{\left||x_{n+1} - x_n |,|y_{n+1}-y_n |\right|}$

Problema resuelto

Problema 1. Hallar los valores de $x$ y $y$ del siguiente sistema de ecuaciones no lineales

Con un punto lineal $(x_0,y_0 )=(3,1)$ y con una tolerancia de 0.10.

Solución. Se asignan las ecuaciones como A y B

Se observa que la ecuación A tiene mayor facilidad para despejar la variable $x$ . Así que, se despejará un término $x$ (que se ubicará en el primer miembro) y lo restante se ubicará en el segundo miembro

$x^2+y^2+8-10x=0$

$\displaystyle x = \frac{-x^2-y^2-8}{-10} = \frac{x^2+y^2+8}{10}$

En el caso de la ecuación B, tiene mayor facilidad para despejar la variable $y$ . Por lo que, se despejará un término $y$ (que se ubicará en el primer miembro) y lo restante se ubicará en el segundo miembro

$xy^2+x+8-10y=0$

$\displaystyle y = \frac{-xy^2-x-8}{-10} = \frac{xy^2+x+8}{10}$

De la primera ecuación, se asigna $F(x,y)$

$\displaystyle x = \frac{x^2+y^2+8}{10}$

$\displaystyle F(x,y) = \frac{x^2+y^2+8}{10}$

Y se deriva la función $F(x,y)$ parcialmente con respecto a $x$ y con respecto a $y$

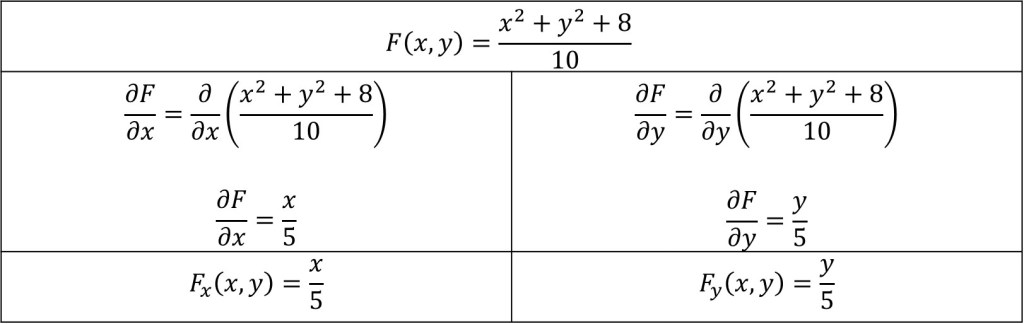
De los resultados de las derivadas parciales, se evalúa con el punto lineal $(x_0, y_0 )=(3,1)$

Y utilizando la fórmula de el criterio de convergencia

$|F_x |+|F_y |<1$

$0.6+0.2<1$

$0.8<1$

De la segunda ecuación, se asigna $G(x,y)$ .

$\displaystyle y = \frac{xy^2+x+8}{10}$

$\displaystyle G(x,y) = \frac{xy^2+x+8}{10}$

Y se deriva la función $G(x,y)$ parcialmente con respecto a $x$ y con respecto a $y$

De los resultados de las derivadas parciales, se evalúa con el punto lineal $(x_0, y_0 )=(3,1)$

\displaystyle G_x (x,y) = \frac{y^2+1}{10}

Y utilizando la fórmula de el criterio de convergencia

$|G_x |+|G_y |<1$

$0.2+0.6<1$

$0.8<1$

Se observa que ambos criterios de convergencia cumplen con la condición, esto quiere decir que los despejes son adecuados y que existe hay solución del sistema de ecuaciones no lineales.

En la primera iteración, se toma la ecuación (A) (donde ya se despejó la variable $x$ ) y se evalúa con el punto lineal $(x_0,y_0 )=(3,1)$ .

$\displaystyle x = F(x,y) = \frac{x^2+y^2+8}{10}$

$x_1 = F(x_0, y_0 ) = F(3,1)$

$\displaystyle x_1 = \frac{(3)^2+(1)^2+8}{10} = \frac{18}{10}$

$x_1 = 1.8$

Del punto $(3,1)$ , el valor de $x_1$ remplazará a $x_0$ , así, el siguiente punto a utilizar será $(1.8, 1)$ . De la ecuación (B) (donde ya se despejó la variable $y$ ), se evalúa con el punto $(1.8, 1)$

$\displaystyle y = G(x,y) = \frac{xy^2+x+8}{10}$

$y_1=G(x_1,y_0 )=G(1.8,1)$

$\displaystyle y_1 = \frac{(1.8) {(1)}^2+1.8+8}{10} = \frac{11.6}{10}$

$y_1 = 1.16$

Entonces, el segundo punto lineal es: $(x_1,y_1 )=(1.8, 1.16)$

Calculando el primer error máximo

$E_1 = \max{\left| |x_1-x_0 |,|y_1-y_0 | \right|}$

$E_1 = \max{\left| |1.8-3|,|1.16-1| \right|}$

$E_1 = \max{\left| |-1.2|, |0.16| \right|}$

$E_1 = \max{|1.2, 0.16|}$

Tomando el valor máximo de $E_1$

$E_1 = 1.2$

Comparando el valor del primer error con el valor de la tolerancia

$E_1 > \text{Tolerancia}$

$1.2 > 0.10$

Como el valor de este error es mayor que la tolerancia, se pasa a la siguiente iteración.

En la segunda iteración, tomando el punto $(x_1,y_1 ) = (1.8, 1.16)$

$x_2 = F(x_1, y_1 ) = F(1.8, 1.16)$

$\displaystyle x_2 = \frac{{(1.8)}^{2}+{(1.16)}^{2}+8}{10}$

$x_2=1.259$

Del punto $(1.8, 1.16)$ , el valor de $x_2$ remplazará a $x_1$ , así, el siguiente punto a utilizar será $(1.259, 1.16)$ . De la ecuación (B) (donde ya se despejó la variable $y$ ), se evalúa con el punto $(1.259, 1.16)$

$y_2 = G(x_2,y_1 ) = G(1.259, 1.16)$

$\displaystyle y_2 = \frac{(1.259) {(1.16)}^{2}+1.259+8}{10}$

$y_2 = 1.095$

Entonces, el tercer punto lineal es: $(x_2,y_2 ) = (1.259, 1.095)$ .

Calculando el segundo error máximo

$E_2 = \max{\left| |x_2-x_1 |,|y_2-y_1 | \right|}$

$E_2 = \max{\left| |1.259-1.8|,|1.095-1.16| \right|}$

$E_2 = \max{\left| |-0.541|, |-0.065| \right|}$

$E_2 = \max{|0.541, 0.065|}$

Tomando el valor máximo de $E_2$ .

$E_2 = 0.541$

Comparando el valor del segundo error con el valor de la tolerancia

$E_2 > \text{Tolerancia}$

$0.541 > 0.10$

Como el valor de este error es mayor que la tolerancia, se pasa a la siguiente iteración.

En la tercera iteración, tomando el punto $(x_2,y_2 ) = (1.259 1.095)$ .

$x_3 = F(x_2, y_2 ) = F(1.259, 1.095)$

$\displaystyle x_3 = \frac{{(1.259)}^{2}+{(1.095)}^{2}+8}{10}$

$x_3=1.078$

Del punto $(1.259, 1.095)$ , el valor de $x_3$ remplazará a $x_2$ , así, el siguiente punto a utilizar será $(1.078, 1.095)$ . De la ecuación (B) (donde ya se despejó la variable $y$ ), se evalúa con el punto $(1.078, 1.095)$ .

$y_3 = G(x_3,y_2 ) = G(1.078, 1.095)$

$\displaystyle y_3 = \frac{(1.078) {(1.095)}^{2}+1.078+8}{10}$

$y_3 = 1.037$

Entonces, el cuarto punto lineal es: $(x_3,y_3 ) = (1.078, 1.037)$ .

Calculando el tercer error máximo

$E_3 = \max{\left| |x_3-x_2 |,|y_3-y_2 | \right|}$

$E_3 = \max{\left| |1.078-1.259|,|1.037-1.095| \right|}$

$E_3 = \max{\left| |-0.181|, |-0.058| \right|}$

$E_3 = \max{|0.181, 0.058|}$

Tomando el valor máximo de $E_3$

$E_3 = 0.181$

Comparando el valor del tercer error con el valor de la tolerancia

$E_3 > \text{Tolerancia}$

$0.181>0.10$

Como el valor de este error es mayor que la tolerancia, se pasa a la siguiente iteración.

En la cuarta iteración, tomando el punto $(x_3,y_3 ) = (1.078, 1.037)$ .

$x_4 = F(x_3, y_3 ) = F(1.078, 1.037)$

$\displaystyle x_4 = \frac{{(1.078)}^{2}+{(1.037)}^{2}+8}{10}$

$x_4=1.024$

Del punto $(1.078, 1.037)$ , el valor de $x_4$ remplazará a $x_3$ , así, el siguiente punto a utilizar será $(1.024, 1.037)$ . De la ecuación (B) (donde ya se despejó la variable $y$ ), se evalúa con el punto $(1.024, 1.037)$

$y_4 = G(x_4,y_3 ) = G(1.024, 1.037)$

$\displaystyle y_4 = \frac{(1.024) {(1.037)}^{2}+1.024+8}{10}$

$y_4 = 1.013$

Entonces, el quinto punto lineal es: $(x_3,y_3 ) = (1.024, 1.013)$ .

Calculando el cuarto error máximo

$E_4 = \max{\left| |x_4-x_3 |,|y_4-y_3 | \right|}$

$E_4 = \max{\left| |1.024-1.078|,|1.013-1.037| \right|}$

$E_4 = \max{\left| |-0.054|, |-0.024| \right|}$

$E_4 = \max{|0.054, 0.024|}$

Tomando el valor máximo de $E_4$

$E_4 = 0.054$

Comparando el valor del cuarto error con el valor de la tolerancia

$E_4 < \text{Tolerancia}$

$0.054<0.10$

Como el valor de este error ya es menor que la tolerancia, el último punto lineal calculado es el resultado final esperado. Finalmente

$\therefore x=1.024 \quad , \quad y=1.013$

$f(x,y)=0$	(A)
$g(x,y)=0$	(B)

$x^2+y^2+8-10x=0$	(A)
$xy^2+x+8-10y = 0$	(B)

$\displaystyle F_x (x,y) = \frac{x}{5}$	$\displaystyle F_y (x,y) = \frac{y}{5}$
$\displaystyle F_x (3,1) = \frac{3}{5} = 0.6$	$\displaystyle F_y (3,1) = \frac{1}{5} = 0.2$

$\displaystyle G_x (x,y) = \frac{y^2+1}{10}$	$\displaystyle G_y (x,y) = \frac{xy}{5}$
$\displaystyle G_x (3,1) = \frac{1}{5} = 0.2$	$\displaystyle G_y (3,1) = \frac{3}{5} = 0.6$

Solución de un sistema de ecuaciones no lineales por el método del punto fijo. Métodos numéricos.

Introducción

Criterio de convergencia

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Solución de un sistema de ecuaciones no lineales por el método del punto fijo. Métodos numéricos.

Introducción

Criterio de convergencia

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta