Función de transferencia de un retenedor de primer orden. Control digital.

A pesar de que los retenedores de primer orden no se utilizan en sistemas de control puede ser de mucha utilidad obtener su función de transferencia. Partiendo de la siguiente ecuación

h(kT+t) = a_n {\tau}^{n} + a_{n-1} {\tau}^{n-1} + \cdots + a_1 \tau + x(kT)

que describe la salida de un circuito de retención de n-ésimo orden. Para el retenedor de primer orden, $n=1$ , se sustituye en la ecuación (1) y se tiene lo siguiente:

donde $0 \le \tau < T$ y $k = 0, 1, 2, ...$ . Al aplicar la condición que establece

$h((k-1)T) = x((k-1)T)$

se puede determinar la constante $a_1$

$h(kT+t) = a_1 \tau + x(kT)$

$h(kT-T) = a_1 (-T) + x(kT)$

$h((k-1)T) = - a_1 T + x(kT)$

$x((k-1)T) = -a_1 T + x(kT)$

$\displaystyle a_1 = \frac{x(kT) - x((k-1)T)}{T}$

Reemplazando el equivalente de $a_1$ en la ecuación (2)

\displaystyle h(kT+t) = \tau \left[\frac{x(kT) - x((k-1)T)}{T} \right] + x(kT)

donde $0 \le \tau < T$ . El proceso de extrapolación del retenedor de primer orden está basado en la ecuación (3). La señal de salida en tiempo continuo $h(t)$ que se obtiene al utilizar el retenedor de primer orden es una señal por secciones.

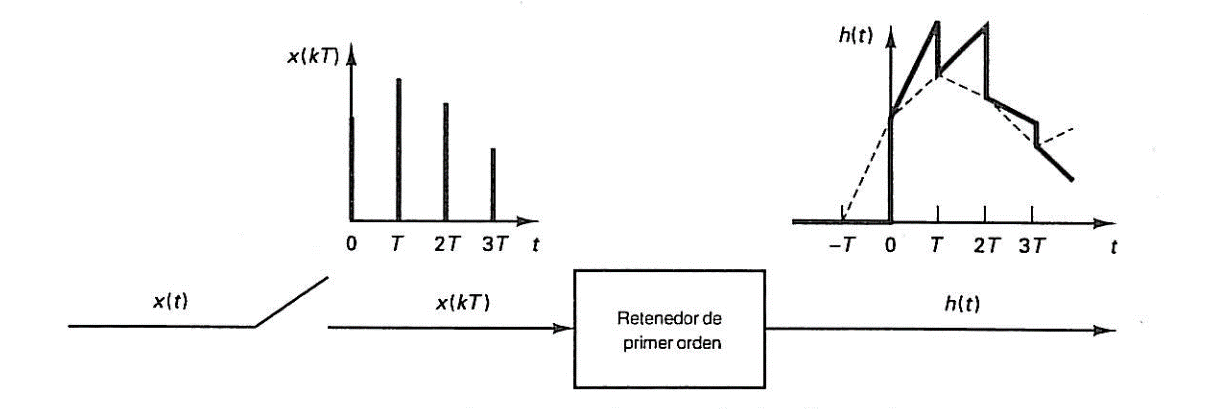
Figura 1. Entrada y salida de un retenedor de primer orden.

Para obtener la función de transferencia del retenedor de primer orden, es conveniente suponer una función sencilla para $x(t)$ , y en nuestro caso, se utilizará la función escalón unitario. Entonces, para el muestreador real y el retenedor de primer orden, la salida $h(t)$ de ese retenedor consiste en líneas rectas que son extrapolaciones de los dos valores muestreados precedentes. La salida $h(t)$ se muestra en el diagrama y su curva puede escribirse de la siguiente manera:

\displaystyle h(t) = (1 + \frac{t}{T}) \cdot 1(t) - \left(\frac{t - T}{T}\right) \cdot 1(t-T) - 1(t-T)

muestreador real en cascada y un retenedor de primer orden — Figura 2. Muestreador real en cascada y un retenedor de primer orden.

La transformada de Laplace de la ecuación (4) es

$\displaystyle \mathcal{L}[h(t)] = \mathcal{L}\left[(1 + \frac{t}{T}) \cdot 1(t) - \left(\frac{t - T}{T}\right) \cdot 1(t-T) - 1(t-T)\right]$

$\displaystyle \mathcal{L}[h(t)] = \mathcal{L}\left[(1 + \frac{t}{T}) \cdot 1(t)\right] - \mathcal{L}\left[\left(\frac{t - T}{T}\right) \cdot 1(t-T)\right] - \mathcal{L}[1(t-T)]$

$\displaystyle H(s) = \left( \frac{1}{s} + \frac{1}{Ts^2} \right) - \frac{1}{Ts^2}\cdot e^{-Ts} - \frac{1}{s}\cdot e^{-Ts}$

\displaystyle H(s) = (1-e^{-Ts})\cdot \frac{Ts + 1}{Ts^2}

Ahora, se tiene un modelo matemático que consiste en un muestreador mediante impulsos y $G_{h1} (s)$ , la función de transferencia del retenedor de primer orden. La señal de salida de este modelo es la misma que la salida del sistema real. Por tanto, la salida $H(S)$ está dada por la ecuación (5).

La transformada de Laplace de la entrada $x^*(t)$ al retenedor de primer orden $G_{h1} (s)$ es

$\displaystyle X^*(s) = \sum_{k=0}^{\infty}{1(kT)e^{-kTs}} = \frac{1}{1-e^{-Ts}}$

Y la función de transferencia $G_{h1}(s)$ del retenedor de primer orden está dada por

$\displaystyle G_{h1}(s) = \frac{H(s)}{X^*(s)}$

$\displaystyle G_{h1}(s) = {(1-e^{-Ts})}^2 \cdot \frac{Ts+1}{Ts^2}$

$\displaystyle G_{h1}(s) = {\left( \frac{1-e^{-Ts}}{s}\right)}^2 \cdot \frac{Ts+1}{T}$

Se observa que un muestreador real en combinación con un retenedor de primer orden es equivalente a un muestreador mediante impulsos con una función de transferencia $\displaystyle {(1-e^{-Ts})}^2 (Ts+1)/(Ts^2)$ .

De manera similar, se pueden obtener las funciones de transferencia de retenedores de alto orden mediante el procedimiento presentado. Sin embargo, puesto que los circuitos de retención de alto orden ( $n \ge 2$ ) no son prácticos desde el punto de vista del retraso (esto puede causar la inestabilidad del sistema) y los efectos del ruido, no se obtendrán sus funciones de transferencia; el retenedor de orden cero es el más práctico y sencillo de manejar.

Función de transferencia de un retenedor de primer orden. Control digital.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Función de transferencia de un retenedor de primer orden. Control digital.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta