Método de la división directa para obtener la transformada z inversa. Control digital.

Introducción

El método de la división directa se obtiene mediante la expansión de $X(z)$ en una serie infinita de potencias de $z^{-1}$ . Este método es útil cuando sea difícil obtener una expresión en forma cerrada para la transformada $z$ inversa o desea encontrar sólo algunos de los primeros términos de $x(k)$ .

El método de la división directa proviene el hecho de que si $X(z)$ está expandida en una serie de potencias de $z^{-1}$ , esto es, si

$\displaystyle X(z) = \sum_{k=0}^{\infty}{x(kT) z^{-k}}$

$\displaystyle X(z) =x(0) + x(T) z^{-1} + x(2T) z^{-2} + ... + x(kT) x^{-k} + ...$

O también

$\displaystyle X(z) =x(0) + x(1) z^{-1} + x(2) z^{-2} + ... + x(k) x^{-k} + ...$

entonces $x(kT)$ o $x(k)$ es el coeficiente del término $z^{-k}$ . Por lo tanto, los valores de $x(kT)$ o $x(k)$ para $k=0,1,2,...$ se pueden determinar por inspección.

Si $X(z)$ está dada en la forma de una función racional, la expansión en una serie de potencias infinita en potencias crecientes de $z^{-1}$ se puede lograr dividir el numerador entre el denominador, donde tanto el numerador como el denominador de $X(z)$ se pueden escribir en potencias crecientes de $z^{-1}$ . Si la serie es convergente, los coeficientes de los términos $z^{-k}$ son los valores de $x(kT)$ de la secuencia del tiempo o los valores de $x(k)$ de la secuencia de números.

Problema resuelto

Problema. Encuente $x(k)$ para $k = 0, 1, 2, 3, 4$ , cuando $X(z)$ está dada por

$\displaystyle X(z) = \frac{10z+5}{(z-1)(z-0.2)}$

Solución. Se reescribe el polinomio del denominador: multiplicando ambos binomios y desarrollar que sus términos sean $z^{-1}$ .

$\displaystyle X(z) = \frac{10z+5}{(z-1)(z-0.2)} \cdot \frac{z^{-2}}{z^{-2}}$

$\displaystyle X(z) = \frac{10z + 5}{z^{2} - 1.2 z + 0.2} \cdot \frac{z^{-2}}{z^{-2}}$

$\displaystyle X(z) = \frac{10z^{-1} + 5z^{-2}}{1 - 1.2 z^{-1} + 0.2 z^{-2}}$

Realizando la división directa

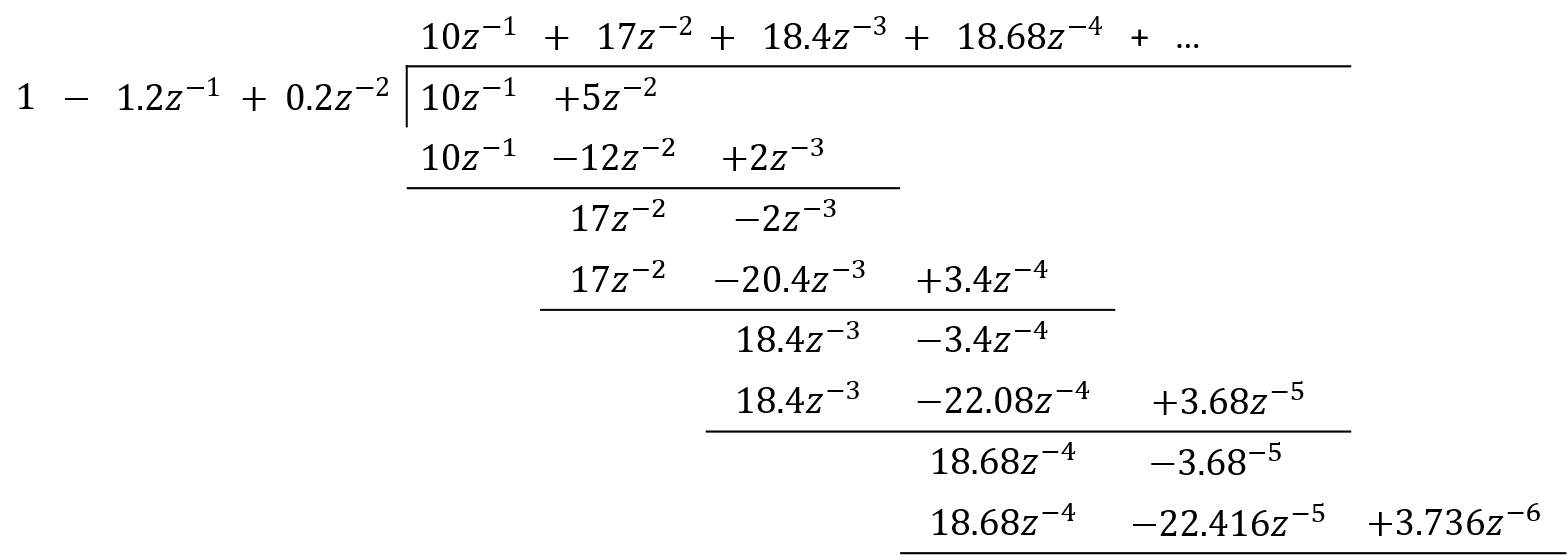
Entonces, la expasión es

$X(z) = 10z^{-1} + 17 z^{-2} + 18.4z^{-3} + 18.68 z^{-4} + \cdots$

Y comparando esta expansión de $X(z)$ en una serie infinita con $\displaystyle X(z) = \sum_{k=0}^{\infty}{x(k)z^{-k}}$ , se obtiene que

$x(0) = 0$

$x(1) = 10$

$x(2) = 17$

$x(3) = 18.4$

$x(4) = 18.68$

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Un comentario sobre “Método de la división directa para obtener la transformada z inversa. Control digital.”

Pingback: Transformada Z Inversa. Solución recurrente | XAE

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.