Filtro pasa-bajas ideal

La amplitud del espectro en frecuencia de un filtro pasa-bajas ideal G_j (j\omega), se muestra en la figura 1. La magnitud del filtro ideal es unitario sobre el intervalo de frecuencias \displaystyle -\frac{1}{2} \omega_S \le \omega \le \frac{1}{2} \omega_s, y es cero fuera de este intervalo de frecuencias.

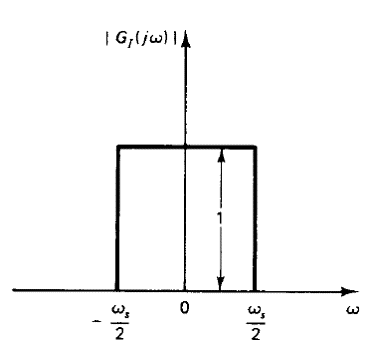
espectro de frecuencia en amplitud de un filtro pasa-bajas ideal
Figura 1. Espectro de frecuencia en amplitud de un filtro pasa-bajas ideal.

El proceso de muestreo introduce un número infinito de componentes complementarias (componentes de bandas laterales) además de la componente primaria. El filtro ideal atenuará todas las componentes complementarias hasta cero y permitirá sólo el paso de la componente primaria, siempre que la \omega_s sea dos veces mayor que la componente de más alta frecuencia de la señal en tiempo continuo. Dicho filtro ideal reconstruye la señal en tiempo continuo representada por las muestras.

Espectro de frecuencia de las señales antes y después del filtrado ideal
Figura 2. Espectro de frecuencia de las señales antes y después del filtrado ideal.

El espectro en frecuencia de salida del filtro ideal es \displaystyle \frac{1}{T} veces el espectro de frecuencia de la señal en tiempo continuo original x(t). Debido a que el filtro ideal tiene características de magnitud constante para la región de frecuencias \displaystyle -\frac{\omega_s}{2} \le \omega \le \frac{\omega_s}{2}, no hay distorsión en ninguna frecuencia dentro de este intervalo. Esto es, no hay corrimiento de fase en el espectro de frecuencia de un filtro ideal. (El corrimiento de fase del filtro ideal es cero.)

En la práctica, el espectro en frecuencia de la señal en tiempo continuo en un sistema de control se puede extender más allá de \displaystyle +\frac{1}{2} \omega_s, incluso cuando las amplitudes a altas frecuencias son pequeñas.

El filtro pasa-bajas no es físicamente realizable

El espectro de frecuencia del filtro ideal es

\displaystyle G_1 (j \omega) = \begin{matrix} 1 & , & - \frac{1}{2} \omega_s \le \omega \le \frac{1}{2} \omega_s \\ 0 & , & \text{en otro caso} \end{matrix}

La transformada inversa de Fourier del espectro en frecuencia G_1 (j\omega) es

\displaystyle \mathcal{F}^{-1} [G_1 (j\omega)] = \frac{1}{2\pi} \int_{-\infty}^{\infty}{G_1 (j\omega) e^{j\omega t} d\omega}

\displaystyle g_1 (t) = \frac{1}{2\pi} \int_{-\infty}^{-\frac{1}{2} \omega_s}{G_1 (j\omega) e^{j\omega t} d\omega} + \frac{1}{2\pi} \int_{-\frac{1}{2} \omega_s}^{\frac{1}{2} \omega_s}{G_1 (j\omega) e^{j\omega t} d\omega} + \frac{1}{2\pi} \int_{\frac{1}{2} \omega_s}^{\infty}{G_1 (j\omega) e^{j\omega t} d\omega}

\displaystyle g_1 (t) = 0 + \frac{1}{2\pi} \int_{-\frac{1}{2} \omega_s}^{\frac{1}{2} \omega_s}{1 \cdot e^{j\omega t} d\omega} + 0 = \frac{1}{2\pi} \int_{-\frac{1}{2} \omega_s}^{\frac{1}{2} \omega_s}{1\cdot e^{j\omega t} d\omega}

\displaystyle g_1 (t) = \frac{1}{2\pi} \cdot \left. (\frac{e^{j\omega t}}{jt}) \right|_{-\frac{1}{2} \omega_s}^{\frac{1}{2} \omega_s} = (\frac{1}{2j \pi t})(e^{j \frac{\omega_s}{2} t} - e^{-j \frac{\omega_s}{2} t})

\displaystyle g_1 (t) = (\frac{1}{t\pi}) (\frac{e^{j \frac{\omega_s}{2} t} - e^{-j \frac{\omega_s}{2} t}}{2j}) = (\frac{1}{t\pi}) \sin{\frac{\omega_s t}{2}}

\displaystyle g_1 (t) ) = \frac{T}{T} (\frac{1}{t\pi}) \sin{\frac{\omega_s t}{2}} = \frac{1}{T} (\frac{1}{t\pi}) \frac{\sin{\frac{\omega_s t}{2}}}{\frac{1}{T}}

\displaystyle g_1 (t) = \frac{1}{T} (\frac{1}{t\pi}) \frac{\sin{\frac{\omega_s t}{2}}}{\frac{\omega_s}{2\pi}} = \frac{1}{T} \frac{\sin{\frac{\omega_s t}{2}}}{\frac{t\omega_s}{2}}

\displaystyle \therefore g_1 (t) = \displaystyle \frac{1}{T} \cdot \frac{\sin{\frac{\omega_s t}{2}}}{\frac{t\omega_s}{2}}

Esta ecuación representa la respuesta impulso unitario, entonces, graficando se tiene la respuesta del filtro ideal.

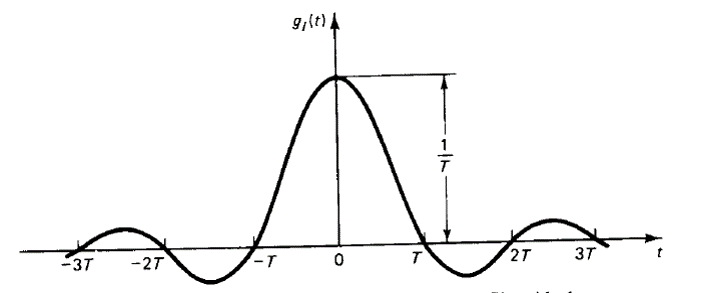
respuesta al impulso g_t (t) de un filtro ideal
Figura 3. Respuesta al impulso g_t (t) de un filtro ideal.

Esta gráfica de g_1 (t) contra t, la respuesta se extiende desde t=-\infty hasta t=\infty. Esto implica que existe respuesta para t<0 a un impulso unitario que se aplica en t=0. (Es decir, la respuesta en el tiempo empieza antes de que aplique la entrada). Esto no puede ser cierto en el mundo físico. Por lo tanto, dicho filtro no es físicamente realizable. En sistemas de control retroalimentado, incrementar el atraso de fase no es deseable desde el punto de vista de la estabilidad. Por lo tanto, se evita agregar atrasos de fase para aproximar al filtro ideal.

Desde el punto de vista práctico, no es posible reconstruir con precisión la señal en tiempo continuo en un sistema de control práctico que éste se ha muestreado.

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.