Continuidad seccional o a trazos

Se dice que una función es seccionalmente continua o continua a trazos en un intervalo \alpha \le t \le \beta si es posible partir el intervalo en un número finito de subintervalos de tal manera que la función sea continua en cada uno de ellos y tenga límites a izquierda y derecha.

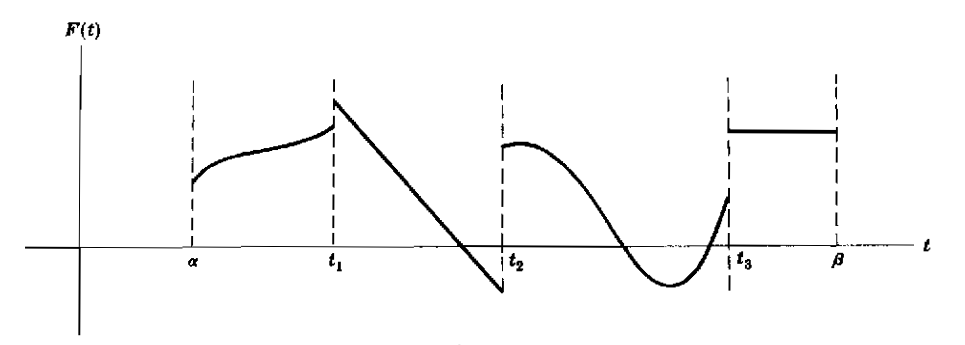
continuidad seccional
Figura 1.2.1 Representación gráfica de una función seccionalmente continua, F(t) = f(t) (R. Spiegel, 1996).

 La función que se muestra en la figura 1 contiene discontinuidades en t_1, t_2 y t_3. Nótese que en t_2, los límites a derecha y a izquierda se representan por

\displaystyle \lim_{\epsilon \rightarrow 0}{f(t_2 + \epsilon)} = f(t_2 + 0) = f(t_2 +)

y

\displaystyle \lim_{\epsilon \rightarrow 0}{f(t_2 - \epsilon)} = f(t_2 - 0) = f(t_2 -)

respectivamente, donde \epsilon es positivo.

Funciones de orden exponencial

Si existen constantes reales  M>0 y \gamma tales que para todo t>N,

|e^{-\gamma t} F(t)|<M   o   |F(t)|<Me^{\gamma t}

se dice que f(t) es una función de orden exponencial \gamma cuando t \rightarrow \infty, o simplemente, que es una función de ordn exponencial.

Condición suficiente para la existencia de la transformada de Laplace.

Existencia de la transformada de Laplace

Teorema. Si f(t) es seccionalmente continua en cada intervalo finito 0 \le t \le N de orden exponencial \gamma$ para t>N, entonces existe la transformada de Laplace F(s) para todo s > \gamma.

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.