Propiedades de la transformada de Laplace. Laplace.

Propiedad de linealidad

Si $c_1$ y $c_2$ son constantes y $f_1 (t)$ y $f_2(t)$ son cuyas transformadas de Laplace son, respectivamente, $F_1 (s)$ y $F_2(s)$ , entonces es

$\displaystyle \mathcal{L} [c_1 f_1 (t) + c_2 f_2 (t)] = c_1 \mathcal{L} [f_1 (t)] + c_2 \mathcal{L} [f_2 (t)]$

O también

$\mathcal{L} [c_1 f_1(t) + c_2 f_2 (t)] = c_1 F_1 (s) + c_2 F_2 (s)$

Demostración

$\displaystyle \mathcal{L} [c_1 f_1(t) + c_2 f_2 (t)] = \int_{0}^{\infty}{e^{-st}[c_1 f_1 (t) + c_2 f_2 (t)] \ dt}$

$\displaystyle \mathcal{L} [c_1 f_1(t) + c_2 f_2 (t)] = \int_{0}^{\infty}{[e^{-st}c_1 f_1 (t) + e^{-st} c_2 f_2 (t)] \ dt}$

$\displaystyle \mathcal{L} [c_1 f_1(t) + c_2 f_2 (t)] = \int_{0}^{\infty}{e^{-st} c_1 f_1 (t) \ dt} + \int_{0}^{\infty}{e^{-st} c_2 f_2 (t) \ dt}$

$\displaystyle \mathcal{L} [c_1 f_1(t) + c_2 f_2 (t)] = c_1 \int_{0}^{\infty}{e^{-st} f_1 (t) \ dt} + c_2 \int_{0}^{\infty}{e^{-st} f_2 (t) \ dt}$

$\displaystyle \mathcal{L} [c_1 f_1 (t) + c_2 f_2 (t)] = c_1 \mathcal{L} [f_1 (t)] + c_2 \mathcal{L} [f_2 (t)]$

$\displaystyle \therefore \mathcal{L} [c_1 f_1(t) + c_2 f_2 (t)] = c_1 F_1 (s) + c_2 F_2 (s)$

Primera propiedad de traslación

Si $\mathcal{L} [f(t)] = F(s)$ entonces

$\mathcal{L} [e^{at} \ f(t)] = F(s-a)$

Demostración

$\displaystyle \mathcal{L}[f(t)] = \int_{0}^{\infty}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L}[e^{at} f(t)] = \int_{0}^{\infty}{e^{-st} \cdot e^{at} f(t) \ dt}$

$\displaystyle \mathcal{L}[e^{at} f(t)] = \int_{0}^{\infty}{e^{-st + at} f(t) \ dt}$

$\displaystyle \mathcal{L}[e^{at} f(t)] = \int_{0}^{\infty}{e^{(-s + a)t} f(t) \ dt}$

$\displaystyle \mathcal{L}[e^{at} f(t)] = \int_{0}^{\infty}{e^{-(s - a)t} f(t) \ dt}$

$\displaystyle \therefore \mathcal{L}[e^{at} f(t)] =F(s-a)$

Segunda propiedad de traslación

Si $f(t) = F(s)$ , para $f(t-a)$ si $t>a$ es

$\mathcal{L} [f(t-a)] = e^{-as} F(s)$

Demostración.

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{\infty}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{a}{e^{-st} f(t) \ dt} + \int_{a}^{\infty}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{a}{e^{-st} (0) \ dt} + \int_{a}^{\infty}{e^{-st} g(t-a) \ dt}$

$\displaystyle \mathcal{L} [f(t)] = \int_{a}^{\infty}{e^{-st} g(t-a) \ dt}$

Tomando la sustitución $t = u+a$ y $dt=du$ (y también $u=t-a$ ), se tiene que

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{\infty}{e^{-s(u+a)} g(u) \ du}$

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{\infty}{e^{-su - as} g(u) \ du}$

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{\infty}{e^{-su} e^{-as} g(u) \ du}$

$\displaystyle \mathcal{L} [f(t)] = e^{-as} \int_{0}^{\infty}{e^{-su} g(u) \ du}$

$\displaystyle \mathcal{L} [f(t)] = e^{-as} G(s)$

Propiedad del cambio de escala

Si $\mathcal{L}[f(t)] = F(s)$ , entonces

$\displaystyle \mathcal{L} [f(at)] = \frac{1}{a} F(\frac{s}{a})$

Demostración

$\displaystyle \mathcal{L}[f(t)] = \int_{0}^{\infty}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L}[f(at)] = \int_{0}^{\infty}{e^{-st} f(at) \ dt}$

Realizando la sustitución $u = at$ y $du = a \ dt$ (y también $\displaystyle t = \frac{u}{a}$ , $dt = 1/a \ du$ ) en el segundo miembro, resulta que

$\displaystyle \mathcal{L}[f(at)] = \int_{0}^{\infty}{e^{-s \ \frac{u}{a}} f(u) \ (\frac{1}{a} \ du)}$

$\displaystyle \mathcal{L}[f(at)] = \frac{1}{a} \int_{0}^{\infty}{e^{- \frac{su}{a}} f(u) \ du}$

$\displaystyle \therefore \mathcal{L}[f(at)] = \frac{1}{a} f \left(\frac{s}{a} \right)$

Transformada de Laplace de las derivadas

1.- Si $\mathcal{L}[f(t)] = F(s)$ , entonces

$\displaystyle \mathcal{L} \left[ \frac{d}{dt} f(t) \right] = s F(s) - f(0)$

si f(t) es continua para $0 \le t \le N$ y de orden exponencial para t>N mientras que f(t) es seccionalmente continua para $0 \le t \le N$ .

2.- Si $f(f)$ no satisface la continuidad en $t=0$ , pero $\displaystyle \lim_{}{f(t)} = f(0+)$ existe (aunque no sea igual a $f(0)$ , el cual, puede o no existir), entonces

$\mathcal{L}[f'(t)] = s \cdot F(s) - f(0+)$

3.- Si $f(t)$ deja de ser continua en $t=a$ , entonces

$\mathcal{L}[f'(t)] = s \cdot F(s) - f(0) - e^{-as}[f(a+) - f(a-)]$

donde $f(a+) - f(a-)$ se llama el salto en la discontinuidad en $t=a$ . Pueden hacerse modificaciones que sean adecuadas para más de un salto.

4.- Si $\mathcal{L}[f(t)] = F(s)$ , entonces

$\mathcal{L}[f(t)] = s^n F(s) - s^{n-1} f(0) - s^{n-2} f'(0) - \cdots - s f^{(n-2)}(0) - f^{(n-1)}(0)$

si $f(t), \cdots , f^{(n-1)}(0)$ son continuas para $0\le t \le N$ y de orden exponencial para $t>N$ , además, si $f^{(n)}(t)$ es seccionalmente continua para $0 \le t \le N$ .

Demostración de la transformada de Laplace de la primera derivada de una función.

$\displaystyle \mathcal{L}[f'(t)] = \int_{0}^{\infty}{e^{-st} f'(t) \ dt}$

$\displaystyle \mathcal{L}[f'(t)] = \lim_{m \rightarrow \infty}{\int_{0}^{m}{e^{-st} f'(t) \ dt}}$

$\displaystyle \mathcal{L}[f'(t)] = \lim_{m \rightarrow \infty}{\left[\left. e^{-st} f(t) \right|_{0}^{m} - \int_{0}^{m}{(-s \cdot e^{-st}) f(t) \ dt} \right]}$

$\displaystyle \mathcal{L}[f'(t)] = \lim_{m \rightarrow \infty}{\left\{ \left[e^{-s \cdot m} f(m) - e^{-s \cdot 0} f(0) \right] + s \int_{0}^{m}{e^{-st} f(t) \ dt} \right\}}$

$\displaystyle \mathcal{L}[f'(t)] = \left[e^{-s \cdot \infty} f(\infty) - e^{0} f(0) \right] + s \int_{0}^{\infty}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L}[f'(t)] = \left[0 - (1) \ f(0) \right] + s \int_{0}^{\infty}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L}[f'(t)] = - f(0) + s \int_{0}^{\infty}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L}[f'(t)] = - f(0) + s \ F(s)$

$\displaystyle \therefore \mathcal{L}[f'(t)] = s \ F(s) - f(0)$

Demostración de la transformada de Laplace de la segunda derivada de una función.

$\displaystyle \mathcal{L}[f''(t)] = \int_{0}^{\infty}{e^{-st} f''(t) \ dt}$

Haciendo $g(t) = f'(t)$ y $g'(t) = f''(t)$ , la expresión toma la siguiente forma

$\displaystyle \mathcal{L}[g'(t)] = \int_{0}^{\infty}{e^{-st} g'(t) \ dt}$

$\displaystyle \mathcal{L}[g'(t)] = \lim_{m \rightarrow \infty}{\int_{0}^{m}{e^{-st} g'(t) \ dt}}$

$\displaystyle \mathcal{L}[g'(t)] = \lim_{m \rightarrow \infty}{\left[\left. e^{-st} g(t) \right|_{0}^{m} - \int_{0}^{m}{(-s \cdot e^{-st}) g(t) \ dt} \right]}$

$\displaystyle \mathcal{L}[g'(t)] = \lim_{m \rightarrow \infty}{\left\{ \left[e^{-s \cdot m} g(m) - e^{-s \cdot 0} g(0) \right] + s \int_{0}^{m}{e^{-st} g(t) \ dt} \right\}}$

$\displaystyle \mathcal{L}[g'(t)] = \left[e^{-s \cdot \infty} g(\infty) - e^{0} g(0) \right] + s \int_{0}^{\infty}{e^{-st} g(t) \ dt}$

$\displaystyle \mathcal{L}[g'(t)] = \left[0 - (1) \ g(0) \right] + s \int_{0}^{\infty}{e^{-st} g(t) \ dt}$

$\displaystyle \mathcal{L}[g'(t)] = - g(0) + s \int_{0}^{\infty}{e^{-st} g(t) \ dt}$

$\displaystyle \mathcal{L}[g'(t)] = - g(0) + s \ G(s)$

$\displaystyle \mathcal{L}[f''(t)] = - f'(0) + s \ F'(s)$

$\displaystyle \mathcal{L}[f''(t)] = - f'(0) + s \int_{0}^{\infty}{e^{-st} f'(t) \ dt}$

$\displaystyle \mathcal{L}[f''(t)] = \lim_{m \rightarrow \infty}{\left[- f'(0) + s \int_{0}^{m}{e^{-st} f'(t) \ dt} \right]}$

$\displaystyle \mathcal{L}[f''(t)] = \lim_{m \rightarrow \infty}{\left\{- f'(0) + s \left[\left. e^{-st} f(t)\right|_{0}^{m} - \int_{0}^{m}{(-s \cdot e^{-st}) f(t) \ dt} \right] \right\}}$

$\displaystyle \mathcal{L}[f''(t)] = - f'(0) + s \left[\left. e^{-st} f(t)\right|_{0}^{\infty} - \int_{0}^{\infty}{(-s \cdot e^{-st}) f(t) \ dt} \right]$

$\displaystyle \mathcal{L}[f''(t)] = - f'(0) + s \left[\left. e^{-st} f(t)\right|_{0}^{\infty} + s \int_{0}^{\infty}{e^{-st} f(t) \ dt} \right]$

$\displaystyle \mathcal{L}[f''(t)] = - f'(0) + s \left\{\left[ e^{-s \cdot \infty} f(\infty) - e^{-s \cdot 0} f(0) \right] + s \int_{0}^{\infty}{e^{-st} f(t) \ dt} \right\}$

$\displaystyle \mathcal{L}[f''(t)] = - f'(0) + s \left\{\left[ e^{-\infty} f(\infty) - e^{0} f(0) \right] + s \int_{0}^{\infty}{e^{-st} f(t) \ dt} \right\}$

$\displaystyle \mathcal{L}[f''(t)] = - f'(0) + s \left\{\left[ (0)- (1) f(0) \right] + s \int_{0}^{\infty}{e^{-st} f(t) \ dt} \right\}$

$\displaystyle \mathcal{L}[f''(t)] = - f'(0) + s \left[- f(0) + s \int_{0}^{\infty}{e^{-st} f(t) \ dt} \right]$

$\displaystyle \mathcal{L}[f''(t)] = - f'(0) - s f(0) + s^2 \int_{0}^{\infty}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L}[f''(t)] = - f'(0) - s f(0) + s^2 F(s)$

$\displaystyle \therefore \mathcal{L}[f''(t)] = s^2 F(s) - s f(0) - f'(0)$

Transformada de Laplace de las integrales

Si $\mathcal{L} [f(t)] = F(s)$ , entonces

$\displaystyle \mathcal{L} \left[\int_{0}^{t}{f(\tau) \ d\tau} \right] = \frac{F(s)}{s}$

Demostración.

Sea $\displaystyle g(t) = \int_{0}^{t}{f(\tau) \ d\tau}$ , $g'(t) = f(t)$ y $g(0) = 0$ . Entonces,

$\displaystyle g'(t) = f(t)$

$\displaystyle \mathcal{L}[g'(t)] = \mathcal{L}[f(t)]$

$\displaystyle s G(s) - g(0) = F(s)$

$\displaystyle s G(s) - 0 = F(s)$

$\displaystyle s G(s) = F(s)$

$\displaystyle G(s) = \frac{F(s)}{s}$

$\displaystyle \mathcal{L} \left[g(t) \right] = \frac{F(s)}{s}$

$\displaystyle \therefore \mathcal{L} \left[ \int_{0}^{\infty}{f(\tau) \ d\tau} \right] = \frac{F(s)}{s}$

Multiplicación por $t^n$

Si $\mathcal{L}[f(t)] = F(s)$ , entonces

$\displaystyle \mathcal{L}[t^n f(t)] = {(-1)}^n \frac{d^n}{ds^n} F(s) = {(-1)}^n F^{(n)} (s)$

Demostración para «t f(t)» (es decir, $n=1$ ).

$\displaystyle F(s) = \int_{0}^{\infty}{e^{-st} f(t) \ dt}$

$\displaystyle \frac{d}{ds}[F(s)] = \frac{d}{ds} \left[\int_{0}^{\infty}{e^{-st} f(t) \ dt} \right]$

$\displaystyle \frac{d}{ds}[F(s)] = \int_{0}^{\infty}{\frac{\partial}{\partial s} [e^{-st} f(t)] \ dt}$

$\displaystyle \frac{d}{ds}[F(s)] = \int_{0}^{\infty}{(-t \cdot e^{-st}) f(t) \ dt}$

$\displaystyle \frac{d}{ds}[F(s)] = - \int_{0}^{\infty}{t e^{-st} f(t) \ dt}$

$\displaystyle \frac{d}{ds}[F(s)] = - \int_{0}^{\infty}{e^{-st} [t \ f(t)] \ dt}$

$\displaystyle \frac{d}{ds}[F(s)] = -\mathcal{L} [t f(t)]$

$\displaystyle -\mathcal{L} [t f(t)] = \frac{d}{ds}[F(s)]$

$\displaystyle \mathcal{L} [t f(t)] = - \frac{d}{ds}[F(s)]$

$\displaystyle \therefore \mathcal{L} [t f(t)] = - F'(s)$

Demostración para « $t^n f(t)$ » (es decir, $n=k+1$ ).

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{\infty}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L} [t f(t)] = - F(s)$

$\displaystyle \mathcal{L} [t f(t)] = (-1) F(s)$

$\displaystyle \mathcal{L} [t^k f(t)] = (-1)^k F^{(k)}(s)$

$\displaystyle \int_{0}^{\infty}{e^{-st} \cdot t^k f(t) \ dt} = (-1)^k F^{(k)}(s)$

$\displaystyle \frac{d}{ds} \left[\int_{0}^{\infty}{e^{-st} \cdot t^k f(t) \ dt} \right] = \frac{d}{ds} \left[(-1)^k F^{(k)}(s) \right]$

$\displaystyle \int_{0}^{\infty}{\frac{\partial}{\partial s}[e^{-st} \cdot t^k f(t)] \ dt} = \left[(-1)^k \cdot F^{(k+1)}(s) \right]$

$\displaystyle \int_{0}^{\infty}{(-t e^{-st}) \cdot t^k f(t) \ dt} = (-1)^k F^{(k+1)}(s)$

$\displaystyle - \int_{0}^{\infty}{e^{-st} \cdot t^{k+1} f(t) \ dt} = (-1)^k F^{(k+1)}(s)$

$\displaystyle (-1) \int_{0}^{\infty}{e^{-st} \cdot t^{k+1} f(t) \ dt} = (-1)^k F^{(k+1)}(s)$

$\displaystyle \int_{0}^{\infty}{e^{-st} \cdot t^{k+1} f(t) \ dt} = \frac{(-1)^k}{(-1)} F^{(k+1)}(s)$

$\displaystyle \int_{0}^{\infty}{e^{-st} \cdot t^{k+1} f(t) \ dt} = (-1)^{k-1} F^{(k+1)}(s)$

$\displaystyle \int_{0}^{\infty}{e^{-st} \cdot t^{k+1} f(t) \ dt} = (-1)^{k+1} F^{(k+1)}(s)$

$\displaystyle \mathcal{L}[t^{k+1} f(t)] = (-1)^{k+1} F^{(k+1)}(s)$

$\displaystyle \mathcal{L}[t^n f(t)] = (-1)^n F^n (s) = (-1)^n \frac{d^n}{ds^n} [F(s)]$

División por $t$

Si $\mathcal{L} \left[f(t) \right] = F(s)$ , entonces

$\displaystyle \mathcal{L} \left[\frac{f(t)}{t} \right] = \int^{\infty}_{s}{f(\sigma) \ d\sigma}$

siempre que exista $\displaystyle \lim_{t \rightarrow 0}{\frac{f(t)}{t}}$ .

$\displaystyle g(t) = \frac{f(t)}{t}$

$\displaystyle t \cdot g(t) = f(t)$

$\displaystyle \mathcal{L}[t g(t)] =\mathcal{L} [f(t)]$

$\displaystyle - \frac{d}{ds} {\mathcal{L} [g(t)]} = \mathcal{L} [f(t)]$

$\displaystyle - \frac{d}{ds} [G(s)] = F(s)$

$\displaystyle d[G(s)] = - F(s) \ ds$

$\displaystyle \int_{\infty}^{s}{d[G(s)]} = - \int_{\infty}^{s}{F(\sigma) \ d\sigma}$

$\displaystyle G(s) = \int_{s}^{\infty}{F(\sigma) \ d\sigma}$

$\displaystyle \mathcal{L}[g(t)] = \int_{s}^{\infty}{F(\sigma) \ d\sigma}$

$\displaystyle \therefore \mathcal{L} \left[\frac{f(t)}{t} \right] = \int_{s}^{\infty}{F(\sigma) \ d\sigma}$

Funciones periódicas

Sea $f(t)$ con período $T>0$ tal que $f(t+T) = f(t)$ . Entonces

$\displaystyle \mathcal{L}[f(t)] = \frac{\int^{T}_{0}{e^{-st} f(\tau) d\tau}}{1-e^{-sT}}$

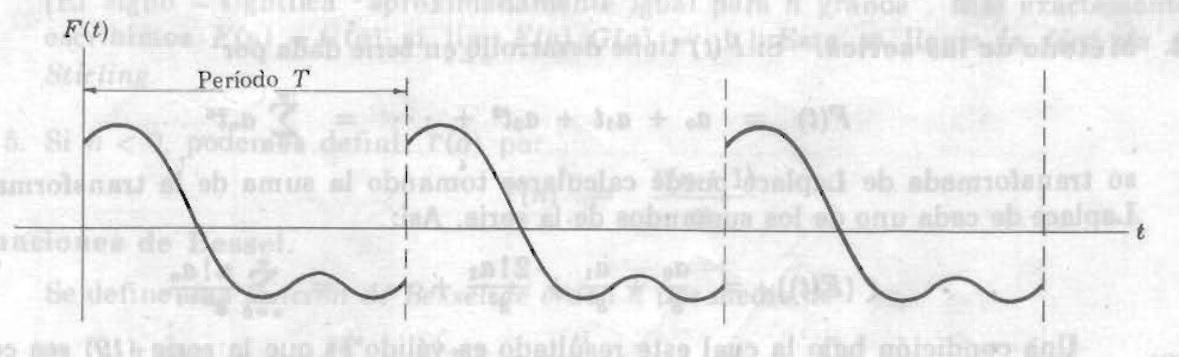
funcion periódica — *Figura 1.3.1 Represencación gráfica de una función peródica (R. Spiegel, 1996).*

Demostración.

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{\infty}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{T}{e^{-st} f(t) \ dt} + \int_{T}^{2T}{e^{-st} f(t) \ dt} + \int_{2T}^{3T}{e^{-st} f(t) \ dt} + \cdots$

Tomando la sustitución: en la primera integral $t=\tau$ y $dt=d\tau$ , en la segunda integral $t=\tau + T$ y $dt=d\tau$ , y en la tercera integral $t= \tau + 2T$ y $dt=d\tau$ , resulta que

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{T}{e^{-s\tau} f(\tau) \ d\tau} + \int_{0}^{T}{e^{-s(\tau+T)} f(\tau +T) \ d\tau} + \int_{0}^{T}{e^{-s(\tau +2T)} f(\tau +2T) \ d\tau} +$

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{T}{e^{-s\tau} f(\tau) \ d\tau} + \int_{0}^{T}{e^{-s\tau -sT} f(\tau +T) \ d\tau} + \int_{0}^{T}{e^{-s\tau -2sT} f(\tau +2T) \ d\tau} +$

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{T}{e^{-s\tau} f(\tau) \ d\tau} + \int_{0}^{T}{e^{-s\tau} e^{-sT} f(\tau+T) \ d\tau} + \int_{0}^{T}{e^{-s\tau} e^{-2sT} f(\tau+2T) \ d\tau} +$

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{T}{e^{-s\tau} f(\tau) \ d\tau} + e^{-sT} \int_{0}^{T}{e^{-s\tau} f(\tau+T) \ d\tau} + e^{-2sT} \int_{0}^{T}{e^{-s\tau} f(\tau+2T) \ d\tau} +$

Como $f(\tau+T)=f(\tau)$ , $f(\tau + 2T) = f(\tau)$ , …, tiene la siguiente expresión

$\displaystyle \mathcal{L} [f(t)] = \int_{0}^{T}{e^{-s\tau} f(\tau) \ d\tau} + e^{-sT} \int_{0}^{T}{e^{-s\tau} f(\tau) \ d\tau} + e^{-2sT} \int_{0}^{T}{e^{-s\tau} f(\tau) \ d\tau} +$

$\displaystyle \mathcal{L} [f(t)] = (1 + e^{-sT} + e^{-2sT} + \cdots) \int_{0}^{T}{e^{-s\tau} f(\tau) \ d\tau}$

$\displaystyle \mathcal{L} [f(t)] = \left( \frac{1}{1-e^{-sT}} \right) \int_{0}^{T}{e^{-s\tau} f(\tau) \ d\tau} = \frac{ \int_{0}^{T}{e^{-s\tau} f(\tau) \ d\tau} }{1-e^{-sT}}$

Comportamiento de F(s) cuando $s \rightarrow \infty$

Si $\mathcal{L}[f(t)]=F(s)$ , entonces

$\displaystyle \lim_{s \rightarrow \infty}{F(s)} = 0$

Teorema del valor inicial

Si existen los límites indicados, entonces

$\displaystyle \lim_{t \rightarrow 0}{f(t)} = \lim_{s \rightarrow \infty}{s F(s)}$

Demostración.

$\displaystyle \mathcal{L}[f'(t)] = s F(s) - f(0)$

$\displaystyle \int_{0}^{\infty}{e^{-st} f'(t) \ dt} = s F(s) - f(0)$

$\displaystyle \lim_{s \rightarrow \infty}{\left[\int_{0}^{\infty}{e^{-st} f'(t) \ dt} \right]} = \lim_{s \rightarrow \infty}{\left[s F(s) - f(0) \right]}$

$\displaystyle \lim_{s \rightarrow \infty}{\left[\int_{0}^{\infty}{e^{-st} f'(t) \ dt} \right]} = \lim_{s \rightarrow \infty}{s F(s)} - \lim_{s \rightarrow \infty}{f(0)}$

$\displaystyle 0 = \lim_{s \rightarrow \infty}{s F(s)} - f(0)$

$\displaystyle 0 = \lim_{s \rightarrow \infty}{s F(s)} - \lim_{t \rightarrow 0}{f(t)}$

$\displaystyle \lim_{t \rightarrow 0}{f(t)} = \lim_{s \rightarrow \infty}{s F(s)}$

Teorema del valor final

Si existen los valores indicados, entonces

$\displaystyle \lim_{t \rightarrow \infty}{f(t)} = \lim_{s \rightarrow 0}{s F(s)}$

Demostración.

$\displaystyle \mathcal{L}[f'(t)] = s F(s) - f(0)$

$\displaystyle \int_{0}^{\infty}{e^{-st} f'(t) \ dt} = s F(s) - f(0)$

$\displaystyle \lim_{s \rightarrow 0}{\left[\int_{0}^{\infty}{e^{-st} f'(t) \ dt} \right]} = \lim_{s \rightarrow 0}{\left[s F(s) - f(0) \right]}$

$\displaystyle \lim_{s \rightarrow 0}{\left[\int_{0}^{\infty}{e^{-st} f'(t) \ dt} \right]} = \lim_{s \rightarrow 0}{s F(s)} - \lim_{s \rightarrow 0}{f(0)}$