Cálculo del área de una función polar. Cálculo integral.

Introducción

De lo que se trata es hallar el área acotada por una curva y dos de sus radios vectores.
Suponiendo que la ecuación de la curva se representa con ρ=f(θ) y los dos radios vectores con $OP_1$ y $OD$ (figura 1).

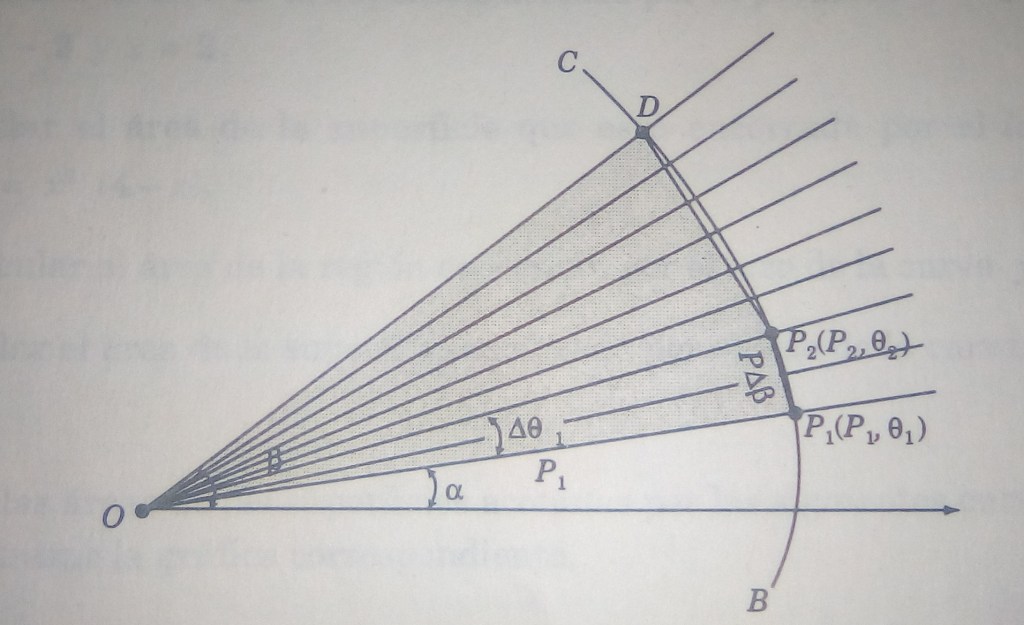
figura 4.5.1 — Figura 1. Representación gráfica de un área acotada por una curva con dos radios vectores.

Sean también α y β los ángulos que forman dichos radios vectores y el eje polar. Aplicando el teorema fundamental del cálculo integral, se tiene que

Primer paso. Con base en la figura 1, el área pedida es el límite de la suma de sus sectores circulares construidos.

Segundo paso. Sean los ángulos centrales de los sectores $\Delta \theta_1$ , $\Delta \theta_2$ , $\Delta \theta_3$ , etc., y sus radios $\rho_1$ , $\rho_2$ , $\rho_3$ , etc. Entonces la suma de las áreas de los sectores es

$\displaystyle \frac{1}{2} \rho_1^2 \Delta \theta_1 + \frac{1}{2} \rho_2^2 \Delta \theta_2 + \frac{1}{2} \rho_3^2 \Delta \theta_3 + \cdots + \frac{1}{2} \rho_n^2 \Delta \theta_n = \sum_{i=1}^n{\frac{1}{2} \rho_i^2 \Delta \theta_i}$

Lo anterior se debe a que el área de un sector circular es igual a ½ del radio por arco; entonces el área del primer sector es igual a $\displaystyle (\frac{1}{2} \rho_1 )(\rho_1 \Delta \theta_1 ) = \frac{1}{2} \rho_1^2 \Delta \theta_1$ .

Tercer paso. Aplicando el teorema fundamental del cálculo integral, resulta

$\displaystyle \lim_{n \rightarrow \infty}{\sum_{i=1}^{n}{\frac{1}{2} \rho_i^2 \Delta \theta_i}} = \int_{\alpha}^{\beta}{\frac{1}{2} \rho^2 \, d\theta} = \frac{1}{2} \int_{\alpha}^{\beta}{\rho^2 \, d\theta}$

Sustituyendo en la ecuación de la curva, el valor de ρ estará en términos de θ.

Por tanto, el elemento de área para $\displaystyle \frac{1}{2} \int_{\alpha}^{\beta}{\rho \, d\theta}$ es un sector circular de radio ρ y el ángulo central dθ.

Por tanto, la fórmula para calcular el área cuando una función es polar es

$\displaystyle \text{Area} = \frac{1}{2} \int_{\alpha}^{\beta}{\rho^2 \, d\theta}$

Problemas resueltos

Problema 1. Hallar el área de la superficie limitada por el círculo $\rho = a \cos{\theta}$ y las rectas θ=0° y θ=60°.

Solución. Se realiza una tabulación desde θ=0° hasta θ=60°, en donde la ecuación $\rho = a \cos{\theta}$ , se considera un valor de $a=1$ , para que sea $\rho = \cos{\theta}$ .

Graficando la función

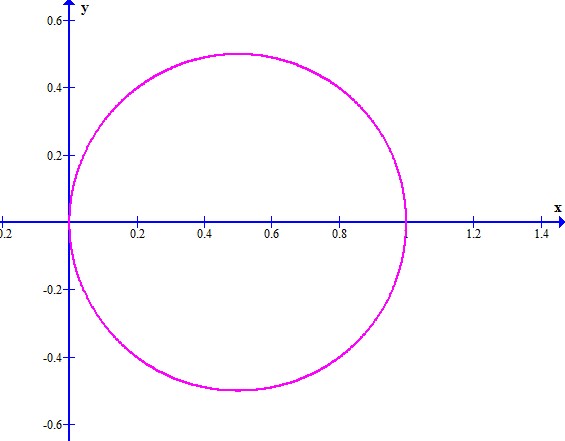
figura 4.5.2 — Figura 2. Gráfica de la función ρ=a cos θ.

Tomando la fórmula y sustituyendo

$\displaystyle \text{Area} = \frac{1}{2} \int_{\alpha}^{\beta}{\rho^2 \, d\theta}$

$\displaystyle \text{Area} = \frac{1}{2} \int_{0}^{60}{(a \cos{\theta})^2 \, d\theta} = \frac{1}{2} a^2 \int_{0}^{60}{\cos^2{\theta} \, d\theta} = \frac{1}{2} a^2 \int_0^{\frac{\pi}{3}}{\cos^2{\theta} \, d\theta}$

$\displaystyle \text{Area} = \frac{1}{2} a^2 \int_0^{\frac{\pi}{3}}{\cos^2{\theta} \, d\theta}$

Resolviéndolo como una integral indefinida

$\displaystyle \int_0^{\frac{\pi}{3}}{\cos^2{\theta} \, d\theta} \quad \rightarrow \quad \int{\cos^2{\theta} \, d\theta}$

Continuando

$\displaystyle \int{\cos^2{\theta} \, d\theta} = \int{(\frac{1}{2} + \frac{1}{2} \cos{2\theta} ) \, d\theta}$

$\displaystyle \int{\cos^2{\theta} \, d\theta} = \frac{1}{2} \int{d\theta} + \frac{1}{2} \int{\cos{2\theta} \, d\theta}$

$\displaystyle \int{\cos^2{\theta} \, d\theta} = \frac{1}{2} \theta + \frac{1}{4} \sin{2\theta} + C$

Regresando y reemplazando la variable θ con sus respectivos límites, resulta

$\displaystyle \int_0^{\frac{\pi}{3}}{\cos^2{\theta} \, d\theta} = \left[\frac{1}{2} \theta + \frac{1}{4} \sin{2\theta} + C\right]_0^{\frac{\pi}{3}}$

$\displaystyle \int_0^{\frac{\pi}{3}}{\cos^2{\theta} \, d\theta} = \left[\frac{1}{2} (\frac{\pi}{3}) + \frac{1}{4} \sin{\frac{2\pi}{3}}\right] - \left[\frac{1}{2} (0) + \frac{1}{4} \sin{0} \right]$

$\displaystyle \int_0^{\frac{\pi}{3}}{\cos^2{\theta} \, d\theta} = \frac{\pi}{6} + \frac{\sqrt{3}}{8}$

Finalmente

$\displaystyle \text{Area} = \frac{1}{2} a^2 \int_0^{\frac{\pi}{3}}{\cos^2{\theta} \, d\theta}$

$\displaystyle \text{Area} = \frac{1}{2} a^2 \left(\frac{\pi}{6} + \frac{\sqrt{3}}{8} \right) \ \text{u}^2 = \frac{a^2 \pi}{12} + \frac{a^2 \sqrt{3}}{16}$

$\displaystyle \therefore \text{Area} = \frac{a^2 \pi}{12} + \frac{a^2 \sqrt{3}}{16} \ \text{u}^2= 0.37 a^2 \ \text{u}^2$

Problema 2. Hallar el área total de la superficie limita por la curva $\rho = a \sin{2\theta}$ .

Solución. Se realiza una tabulación para la curva dada, con la finalidad de determinar los límites inferior y superior. Considerando $a=1$ de la ecuación de la curva, resulta

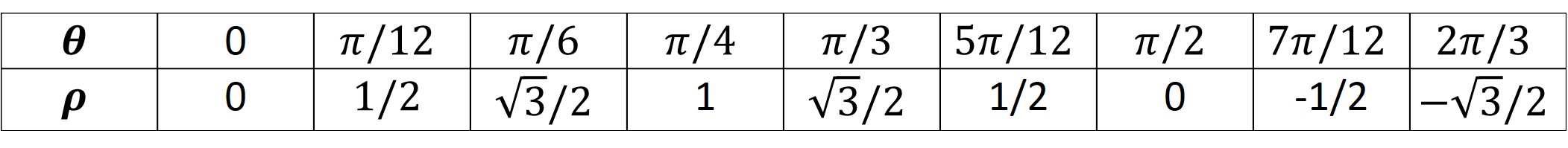
Graficando la función, se tiene lo siguiente

figura 4.5.3 — Figura 3. Representación gráfica de la función brindada por el problema.

El primer pétalo se forma desde $\theta =0$ hasta $\displaystyle \theta = \frac{\pi}{2}$ , el segundo se forma desde $\displaystyle \theta = \frac{\pi}{2}$ hasta $\theta=\pi$ , el tercero se forma desde $\theta=\pi$ hasta $\displaystyle \theta = \frac{3\pi}{2}$ y el último va desde $\displaystyle \theta=\frac{3\pi}{2}$ hasta $\displaystyle \theta=2\pi$ . Entonces, se determinará el área de un solo pétalo y luego se multiplicará cuatro veces para conocer el área total de esa curva.

figura 4.5.4 — Figura 4.5.4 Representación gráfica del área a calcular.

Continuando

$\displaystyle \text{Area} = \frac{1}{2} \int_{\alpha}^{\beta}{\rho^2 \, d\theta} = \frac{1}{2} \left[4\int_0^{\frac{\pi}{2}}{(a \sin{2\theta})^2 \, d\theta} \right]$

$\displaystyle \text{Area} = 2a^2 \int_0^{\frac{\pi}{2}}{\sin^2{2\theta} \, d\theta}$

Resolviéndolo como una integral indefinida

$\displaystyle \int_0^{\frac{\pi}{2}}{\sin^2{2\theta} \, d\theta} \quad \rightarrow \quad \int{\sin^2{2\theta} \, d\theta}$

Continuando

$\displaystyle \int{\sin^2{2\theta} \, d\theta} = \int{\left(\frac{1}{2} - \frac{1}{2} \cos{2\theta} \right) d\theta}$

$\displaystyle \int{\sin^2{2\theta} \, d\theta} = \frac{1}{2} \int{d\theta} - \frac{1}{2} \int{\cos{2\theta} \, d\theta}$

$\displaystyle \int{\sin^2{2\theta} \, d\theta} = \frac{1}{2} \theta - \frac{1}{4} \sin{2\theta} + C$

Regresando y reemplazando la variable θ con sus respectivos límites, resulta

$\displaystyle \int_0^{\frac{\pi}{2}}{\sin^2{2\theta} \, d\theta} = \left[\frac{1}{2} \theta - \frac{1}{4} \sin{2\theta} + C\right]_0^{\frac{\pi}{2}}$

$\displaystyle \int_0^{\frac{\pi}{2}}{\sin^2{2\theta} \, d\theta} = \left[\frac{1}{2} (\frac{\pi}{2}) - \frac{1}{4} \sin{2(\frac{\pi}{2})} \right] - 2a^2 \left[\frac{1}{2} (0) - \frac{1}{4} \sin{2(0)} \right]$

$\displaystyle \int_0^{\frac{\pi}{2}}{\sin^2{2\theta} \, d\theta} = \frac{\pi}{4} - 0 = \frac{\pi}{4}$

Finalmente

$\displaystyle \text{Area} = 2a^2 \int_0^{\frac{\pi}{2}}{\sin^2{2\theta} \, d\theta}$

$\displaystyle \text{Area} = 2a^2 \left( \frac{\pi}{4} \right)$

$\displaystyle \therefore \text{Area} = \frac{\pi}{2} a^2 \ \text{u}^2$

Problema 3. Hallar el área de la superficie encerrada por la curva $\displaystyle \rho = a(1-\cos{\theta})$ .

Solución. Se realiza una tabulación para la curva dada, con la finalidad de determinar los límites inferior y superior. Considerando $a=1$ de la ecuación de la curva, resulta

Graficando la función, se tiene lo siguiente

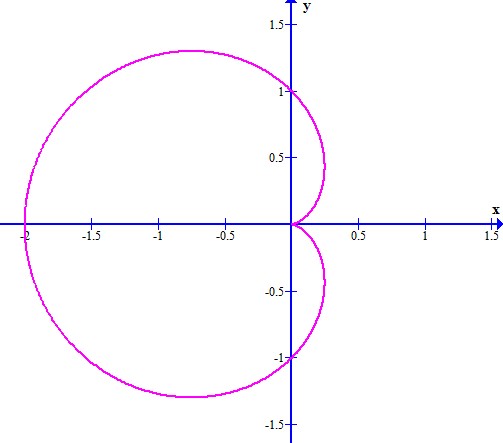
figura 4.5.5 — Figura 5. Gráfica de la función ρ = a(1 – cos θ).

La curva se forma desde θ=0 hasta θ=π, pero es simétrica con respecto al eje x, por tanto, el área a determinar variará desde θ=0 hasta θ=π y después se multiplicará por dos para tomar el área total.

figura 4.5.6 — Figura 6. Representación gráfica de la región a calcular.

Entonces

$\displaystyle \text{Area} = \frac{1}{2} \int_{\alpha}^{\beta}{\rho^2 \, d\theta}$

$\displaystyle \text{Area} = \frac{1}{2} \left[2\int_0^{\pi}{\left[a(1 - \cos{\theta}) \right]^2 \, d\theta} \right]$

$\displaystyle \text{Area} = a^2 \int_0^{\pi}{(1-2 \cos{\theta} + \cos^2{\theta} ) \, d\theta}$

Resolviendo la integral

$\displaystyle \int_0^{\pi}{(1-2 \cos{\theta} + \cos^2{\theta} ) \, d\theta} \quad \rightarrow \quad \int{(1-2 \cos{\theta} + \cos^2{\theta}) \, d\theta}$

Continuando

$\displaystyle \int{(1-2 \cos{\theta} + \cos^2{\theta}) \, d\theta} = \int{d\theta} - 2\int{\cos{\theta} \, d\theta} + \int{cos^2{\theta} \, d\theta}$

$\displaystyle \int{(1-2 \cos{\theta} + \cos^2{\theta}) \, d\theta} = \int{d\theta} - 2\int{\cos{\theta} \, d\theta} + \int{\left(\frac{1}{2} + \frac{1}{2} \cos{2\theta} \right) \, d\theta}$

$\displaystyle \int{(1-2 \cos{\theta} + \cos^2{\theta}) \, d\theta} = \frac{3}{2} \int{d\theta} - 2\int{\cos{\theta} \, d\theta} + \frac{1}{2} \int{\cos{2\theta} \, d\theta}$

$\displaystyle \int{(1-2 \cos{\theta} + \cos^2{\theta}) \, d\theta} = \frac{3}{2} \theta - 2 \sin{\theta} + \frac{1}{4} \sin{2\theta} + C$

Regresando y reemplazando la variable θ con sus respectivos límites, resulta

$\displaystyle \int_0^{\pi}{(1 - 2 \cos{\theta} + \cos^2{\theta}) \, d\theta} = \left[\frac{3}{2} \theta - 2 \sin{\theta} + \frac{1}{4} \sin{2\theta} + C\right]_0^{\pi}$

$\displaystyle \int_0^{\pi}{(1 - 2 \cos{\theta} + \cos^2{\theta}) \, d\theta} = \left[\frac{3}{2} (\pi) - 2 \sin{\pi} + \frac{1}{4} \sin{2\pi} \right] - \left[\frac{3}{2} (0) - 2 \sin{0} + \frac{1}{4} \sin{0} \right]$