Determinando la serie de Fourier de una función “f(t)”. Fourier.

A continuación, se muestra un bloque de problemas resueltos que ayudan a determinar la serie de Fourier de una función $f(t)$ .

Problemas resueltos

Problema 1. Encontrar la serie de Fourier para la función $f(t)$ definida por

$\displaystyle f(t) =\left\{ \begin{matrix} -1 \, , \quad \quad -\frac{T}{2} < t < 0 \\ 1, \, \quad \quad \quad 0 < t < \frac{T}{2} \end{matrix} \right.$

y $f(t + T) = f(t)$ .

Solución. De la serie de Fourier

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{\omega_0 t}+b_n \sin{\omega_0 t})}$

Se va a determinar el valor de $a_0$ . Entonces

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \, dt}$

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{0}{(-1) \, dt} + \frac{2}{T} \int_{0}^{T/2}{(1) \, dt}$

$\displaystyle a_0 = - \frac{2}{T} \int_{-T/2}^{0}{dt} + \frac{2}{T} \int_{0}^{T/2}{dt} = -\frac{2}{T} [t + C]_{-T/2}^{0} + \frac{2}{T} [t + C]_{0}^{T/2}$

$\displaystyle a_0 = -\frac{2}{T} \left[0 - (-\frac{T}{2}) \right] + \frac{2}{T} \left(\frac{T}{2} - 0\right) = -\frac{2}{T} \left(\frac{T}{2} \right) + \frac{2}{T} \left(\frac{T}{2}\right)$

$a_0 = - 1 + 1$

$\displaystyle a_0 = 0$

Después, se calcula el valor de $a_n$

$\displaystyle a_n = \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \cdot \cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \frac{2}{T} \int_{-T/2}^{0}{(-1) \cdot \cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{(1) \cdot \cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = - \frac{2}{T} \int_{-T/2}^{0}{\cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{\cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = - \frac{2}{T} \left[\frac{1}{n \omega_0} \sin{n \omega_0 t} + C \right]_{-T/2}^{0} + \frac{2}{T} \left[\frac{1}{n \omega_0} \sin{n \omega_0 t} + C \right]_{0}^{T/2}$

$\displaystyle a_n = - \frac{2}{T} \left[\frac{1}{n \omega_0} \sin{(n \omega_0 \cdot 0)} - \frac{1}{n \omega_0} \sin{(n \omega_0 \cdot (-\frac{T}{2}))} \right] + \frac{2}{T} \left[\frac{1}{n \omega_0} \sin{(n \omega_0 (\frac{T}{2}))} - \frac{1}{n \omega_0} \sin{(n \omega_0 \cdot 0)} \right]$

$\displaystyle a_n = - \frac{2}{T} \left[- \frac{1}{n \omega_0} \sin{(n \omega_0 \cdot (-\frac{T}{2}))} \right] + \frac{2}{T} \left[\frac{1}{n \omega_0} \sin{(n \omega_0 (\frac{T}{2}))} \right]$

Sabiendo que $\displaystyle \omega_0 = \frac{2\pi}{T}$

$\displaystyle a_n = - \frac{2}{T} \left[- \frac{1}{n \cdot \frac{2\pi}{T}} \sin{(n \frac{2\pi}{T} \cdot (-\frac{T}{2}))} \right] + \frac{2}{T} \left[\frac{1}{n \cdot \frac{2\pi}{T}} \sin{(n \frac{2\pi}{T} (\frac{T}{2}))} \right]$

$\displaystyle a_n = - \frac{2}{T} \left[- \frac{T}{2n\pi} \sin{(-n \pi)} \right] + \frac{2}{T} \left[\frac{T}{2n \pi} \sin{(n \pi)} \right]$

$\displaystyle = - \frac{1}{n \pi} \sin{(n \pi)} + \frac{1}{n \pi} \sin{(n \pi)} = 0$

$a_n = 0$

Luego, se determina el valor de $b_n$

$\displaystyle b_n = \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \cdot \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{2}{T} \int_{-T/2}^{0}{(-1) \cdot \sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{(1) \cdot \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = - \frac{2}{T} \int_{-T/2}^{0}{\sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{\sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = - \frac{2}{T} \left[-\frac{1}{n \omega_0} \cos{n \omega_0 t} \right]_{-T/2}^{0} + \frac{2}{T} \left[-\frac{1}{n \omega_0} \cos{n \omega_0 t} \right]_{0}^{T/2}$

$\displaystyle b_n = - \frac{2}{T} \left[-\frac{1}{n \omega_0} \cos{(n \omega_0 (0))} - \left(-\frac{1}{n \omega_0} \cos{(n \omega_0 (-\frac{T}{2}))} \right) \right] + \frac{2}{T} \left[-\frac{1}{n \omega_0} \cos{(n \omega_0 (\frac{T}{2}))} - \left(-\frac{1}{n \omega_0} \cos{(n \omega_0 (0))}\right) \right]$

$\displaystyle b_n = - \frac{2}{T} \left[-\frac{1}{n \omega_0} (1) - \left(-\frac{1}{n \omega_0} \cos{(n \frac{2\pi}{T} (-\frac{T}{2}))} \right) \right] + \frac{2}{T} \left[-\frac{1}{n \omega_0} \cos{(n \frac{2\pi}{T} (\frac{T}{2}))} - \left(-\frac{1}{n \omega_0 } (1) \right) \right]$

$\displaystyle b_n = - \frac{2}{T} \left[-\frac{1}{n \omega_0}- \left(-\frac{1}{n \omega_0} \cos{(-n \pi)} \right) \right] + \frac{2}{T} \left[-\frac{1}{n \omega_0} \cos{(n \pi)} - \left(-\frac{1}{n \omega_0 } \right) \right]$

$\displaystyle b_n = - \frac{2}{T} \left[-\frac{1}{n \omega_0} + \frac{1}{n \omega_0} \cos{(-n \pi)} \right] + \frac{2}{T} \left[-\frac{1}{n \omega_0} \cos{(n \pi)} + \frac{1}{n \omega_0 } \right]$

$\displaystyle b_n = - \frac{2}{T} \left(-\frac{1}{n \omega_0} + \frac{1}{n \omega_0} \cos{n \pi} \right) + \frac{2}{T} \left(-\frac{1}{n \omega_0} \cos{n \pi} + \frac{1}{n \omega_0 } \right)$

$\displaystyle b_n = - \frac{2}{T} \left(-\frac{1}{n \cdot \frac{2\pi}{T}} + \frac{1}{n \cdot \frac{2\pi}{T}} \cos{n \pi} \right) + \frac{2}{T} \left(-\frac{1}{n \cdot \frac{2\pi}{T}} \cos{n \pi} + \frac{1}{n \cdot \frac{2\pi}{T}} \right)$

$\displaystyle b_n = - \frac{2}{T} \left(-\frac{T}{2 \pi n} + \frac{T}{2\pi n} \cos{n \pi} \right) + \frac{2}{T} \left(-\frac{T}{2\pi n} \cos{n \pi} + \frac{T}{2 \pi n} \right)$

$\displaystyle b_n = \frac{1}{\pi n} - \frac{1}{\pi n} \cos{n \pi} - \frac{1}{\pi n} \cos{n \pi} + \frac{1}{\pi n} = \frac{2}{\pi n} - \frac{2}{\pi n} \cos{n \pi}$

Si $n = 1, 3, 5, 7, \cdots$

$\displaystyle \frac{2}{\pi n} - \frac{2}{\pi n} \cos{n \pi} = \frac{2}{\pi n} - \frac{2}{\pi n} (-1) = \frac{2}{\pi n} + \frac{2}{\pi n} = \frac{4}{\pi n}$

Si $n = 2, 4, 6, 8, \cdots$

$\displaystyle \frac{2}{\pi n} - \frac{2}{\pi n} \cos{n \pi} = \frac{2}{\pi n} - \frac{2}{\pi n} (1) = \frac{2}{\pi n} - \frac{2}{\pi n} = 0$

Entonces

$\displaystyle b_n = \frac{4}{\pi n}$

donde $n=1, 3, 5, 7, \cdots$ .

Finalmente, sustituyendo los valores de cada coeficiente en la serie de Fourier

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{\omega_0 t}+b_n \sin{\omega_0 t})}$

$\displaystyle f(t) = \frac{1}{2} (0) + \sum_{n=impar}^{\infty}{\left[ (0) \cos{\omega_0 t} + (\frac{4}{\pi n}) \sin{\omega_0 t} \right]}$

$\displaystyle \therefore f(t) = \frac{4}{\pi} \sum_{n=impar}^{\infty}{\frac{1}{n} \sin{\omega_0 t}}$

Problema 2. Obtener la serie de Fourier de la siguiente figura

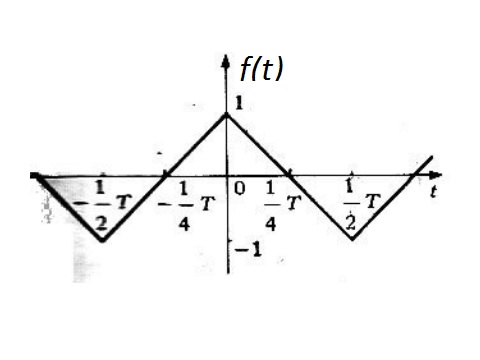
Solución. Analizando la gráfica, en $\displaystyle -\frac{T}{2} < t \le 0$ , $f(t)$ es

$\displaystyle f(t) - f(t_0) = \frac{f(t_1) - f(t_0)}{t_1 - t_0} (t - t_0)$

$\displaystyle f(t) - (-1) = \frac{(1) - (-1)}{0 - (-\frac{T}{2})} (t - (-\frac{T}{2}))$

$\displaystyle f(t) + 1 = \frac{1 + 1}{\frac{T}{2}} (t + \frac{T}{2})$

$\displaystyle f(t) + 1 = \frac{2}{\frac{T}{2}} (t + \frac{T}{2})$

$\displaystyle f(t) + 1 = \frac{4}{T} (t + \frac{T}{2})$

$\displaystyle f(t) + 1 = \frac{4}{T} t + 2$

$\displaystyle f(t) = \frac{4}{T} t + 1$

Y en $\displaystyle 0 \le t < \frac{T}{2}$ , $f(t)$ es

$\displaystyle f(t) - f(t_0) = \frac{f(t_1) - f(t_0)}{t_1 - t_0} (t - t_0)$

$\displaystyle f(t) - (1) = \frac{(-1) - (1)}{\frac{T}{2} - 0} (t - 0)$

$\displaystyle f(t) - 1 = \frac{-1 - 1}{\frac{T}{2}} (t)$

$\displaystyle f(t) - 1 = \frac{-2}{\frac{T}{2}} t$

$\displaystyle f(t) - 1 = -\frac{4}{T} t$

$\displaystyle f(t) - 1 = - \frac{4}{T} t$

$\displaystyle f(t) = - \frac{4}{T} t + 1$

Por esa parte, $f(t)$ esta definida de la siguiente manera

$\displaystyle f(t) = \left\{ \begin{matrix} \frac{4}{T} t + 1 \, , \quad \quad -\frac{T}{2} < t \le 0 \\ - \frac{4}{T} t + 1, \, \quad \quad 0 \le t < \frac{T}{2} \end{matrix} \right.$

Depués, recordando la serie de Fourier

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{\omega_0 t}+b_n \sin{\omega_0 t})}$

Calculando $a_0$

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \, dt}$

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{0}{\left( \frac{4}{T} t + 1 \right) \, dt} + \frac{2}{T} \int_{0}^{T/2}{\left(-\frac{4}{T} t + 1 \right) \, dt}$

$\displaystyle a_0 = \frac{2}{T} \cdot \frac{4}{T} \int_{-T/2}^{0}{t \, dt} + \frac{2}{T} \int_{-T/2}^{0}{dt} - \frac{2}{T} \cdot \frac{4}{T} \int_{0}^{T/2}{t \, dt} + \frac{2}{T} \int_{0}^{T/2}{dt}$

$\displaystyle a_0 = \frac{8}{T^2} \int_{-T/2}^{0}{t \, dt} + \frac{2}{T} \int_{-T/2}^{0}{dt} - \frac{8}{T^2} \int_{0}^{T/2}{t \, dt} + \frac{2}{T} \int_{0}^{T/2}{dt}$

$\displaystyle a_0 = \frac{8}{T^2} \int_{-T/2}^{0}{t \, dt} - \frac{8}{T^2} \int_{0}^{T/2}{t \, dt} + \frac{2}{T} \int_{-T/2}^{0}{dt} + \frac{2}{T} \int_{0}^{T/2}{dt}$

$\displaystyle a_0 = \frac{8}{T^2} \int_{-T/2}^{0}{t \, dt} - \frac{8}{T^2} \int_{0}^{T/2}{t \, dt} + \frac{2}{T} \int_{-T/2}^{T/2}{dt}$

$\displaystyle a_0 = \frac{8}{T^2} \left[ \frac{1}{2} t^2 + C \right]_{-T/2}^{0} - \frac{8}{T^2} \left[ \frac{1}{2} t^2 + C \right]_{0}^{T/2} + \frac{2}{T} [t + C]_{-T/2}^{T/2}$

$\displaystyle a_0 = \frac{8}{T^2} \left[\frac{1}{2} (0)^2 - \frac{1}{2} (-\frac{T}{2})^2\right] - \frac{8}{T^2} \left[ \frac{1}{2} (\frac{T}{2})^2 - \frac{1}{2} (0)^2 \right] + \frac{2}{T} \left[\frac{T}{2} - (-\frac{T}{2}) \right]$

$\displaystyle a_0 = \frac{8}{T^2} \left[- \frac{1}{2} \left( \frac{T^2}{4} \right) \right] - \frac{8}{T^2} \left[ \frac{1}{2} \left(\frac{T^2}{4} \right) \right] + \frac{2}{T} \left(\frac{T}{2} + \frac{T}{2} \right)$

$\displaystyle a_0 = \frac{8}{T^2} \left(- \frac{T^2}{8} \right) - \frac{8}{T^2} \left(\frac{T^2}{8} \right) + \frac{2}{T} (T) = -1 -1 +2$

$a_0 = 0$

Calculando $a_n$ , resulta

$\displaystyle a_n = \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \frac{2}{T} \int_{-T/2}^{0}{\left(\frac{4}{T} t + 1 \right) \cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{\left(-\frac{4}{T} t + 1 \right) \cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \frac{2}{T} \cdot \frac{4}{T} \int_{-T/2}^{0}{t \cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{-T/2}^{0}{\cos{n \omega_0 t} \, dt} - \frac{2}{T} \cdot \frac{4}{T} \int_{0}^{T/2}{t \cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{\cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \frac{8}{T^2} \int_{-T/2}^{0}{t \cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{-T/2}^{0}{\cos{n \omega_0 t} \, dt} - \frac{8}{T^2} \int_{0}^{T/2}{t \cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{\cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \frac{8}{T^2} \int_{-T/2}^{0}{t \cos{n \omega_0 t} \, dt} - \frac{8}{T^2} \int_{0}^{T/2}{t \cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{-T/2}^{0}{\cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{\cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \frac{8}{T^2} \int_{-T/2}^{0}{t \cos{n \omega_0 t} \, dt} - \frac{8}{T^2} \int_{0}^{T/2}{t \cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{-T/2}^{T/2}{\cos{n \omega_0 t} \, dt}$

De la primera y segunda integral

$\displaystyle \int{t \cos{n \omega_0 t} \, dt}$

se resuelve por el método de integración por partes (donde $u=t$ , $du=dt$ , $dv=\cos{n \omega_0 t}$ y $v = \frac{1}{n \omega_0} \sin{n \omega_0 t}$ ). Entonces

$\displaystyle \int{t \cos{n \omega_0 t} \, dt} = (t) \left( \frac{1}{n \omega_0} \sin{n \omega_0 t} \right) - \int{\left(\frac{1}{n \omega_0} \sin{n \omega_0 t} \right)dt}$

$\displaystyle \int{t \cos{n \omega_0 t} \, dt} = \frac{1}{n \omega_0} t \sin{n \omega_0 t} - \frac{1}{n \omega_0} \int{\sin{n \omega_0 t} \, dt}$

$\displaystyle \int{t \cos{n \omega_0 t} \, dt} = \frac{1}{n \omega_0} t \sin{n \omega_0 t} + \frac{1}{n^2 \omega_0^2} \cos{n \omega_0 t} + C$

Para la tercera integral, se toma la propiedad de ortogonalidad

$\displaystyle \frac{2}{T} \int_{-T/2}^{T/2}{\cos{n \omega_0 t} \, dt} = 0$

Regresando y remplazando la variable $t$ por sus respectivos límites interior y superior, resulta lo siguiente

$\displaystyle a_n = \frac{8}{T^2} \int_{-T/2}^{0}{t \cos{n \omega_0 t} \, dt} - \frac{8}{T^2} \int_{0}^{T/2}{t \cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{-T/2}^{T/2}{\cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \frac{8}{T^2} \left[ \frac{1}{n \omega_0} t \sin{n \omega_0 t} + \frac{1}{n^2 \omega_0^2} \cos{n \omega_0 t} + C \right]_{-T/2}^{0} - \frac{8}{T^2} \left[ \frac{1}{n \omega_0} t \sin{n \omega_0 t} + \frac{1}{n^2 \omega_0^2} \cos{n \omega_0 t} + C \right]_{0}^{T/2} + \frac{2}{T}(0)$

$\displaystyle a_n = \frac{8}{T^2} \left[ \left(\frac{1}{n \omega_0} (0) \sin{n \omega_0 (0)} + \frac{1}{n^2 \omega_0^2} \cos{n \omega_0 (0)} \right) - \left(\frac{1}{n \omega_0} (-\frac{T}{2}) \sin{(n \omega_0 (-\frac{T}{2}) )} + \frac{1}{n^2 \omega_0^2} \cos{n \omega_0 (-\frac{T}{2}))} \right) \right] - \frac{8}{T^2} \left[ \left(\frac{1}{n \omega_0} (\frac{T}{2}) \sin{(n \omega_0 (\frac{T}{2}) )} + \frac{1}{n^2 \omega_0^2} \cos{n \omega_0 (\frac{T}{2}))} \right) - \left(\frac{1}{n \omega_0} (0) \sin{n \omega_0 (0)} - \frac{1}{n^2 \omega_0^2} \cos{n \omega_0 (0)} \right) \right] + 0$

$\displaystyle a_n = \frac{8}{T^2} \left[\frac{1}{n^2 \omega_0^2} (1) - \left(\frac{1}{n \omega_0} (-\frac{T}{2}) \sin{(n \omega_0 (-\frac{T}{2}) )} + \frac{1}{n^2 \omega_0^2} \cos{n \omega_0 (-\frac{T}{2}))} \right) \right] - \frac{8}{T^2} \left[ \left(\frac{1}{n \omega_0} (\frac{T}{2}) \sin{(n \omega_0 (\frac{T}{2}) )} + \frac{1}{n^2 \omega_0^2} \cos{n \omega_0 (\frac{T}{2}))} \right) - \frac{1}{n^2 \omega_0^2} (1) \right]$

$\displaystyle a_n = \frac{8}{T^2} \left[\frac{1}{n^2 \omega_0^2} - \left(-\frac{T}{2n \omega_0} \sin{(n (\frac{2\pi}{T}) (-\frac{T}{2}) )} + \frac{1}{n^2 \omega_0^2} \cos{(n (\frac{2\pi}{T}) (-\frac{T}{2}))} \right) \right] - \frac{8}{T^2} \left[ \left(\frac{T}{2n \omega_0} \sin{(n (\frac{2\pi}{T}) (\frac{T}{2}) )} + \frac{1}{n^2 \omega_0^2} \cos{(n (\frac{2\pi}{T}) (\frac{T}{2}))} \right) - \frac{1}{n^2 \omega_0^2} \right]$

$\displaystyle a_n = \frac{8}{T^2} \left[\frac{1}{n^2 \omega_0^2} - \left(-\frac{T}{2n \omega_0} \sin{(-n \pi)} + \frac{1}{n^2 \omega_0^2} \cos{(-n\pi)} \right) \right] - \frac{8}{T^2} \left[ \left(\frac{T}{2n \omega_0} \sin{(n \pi)} + \frac{1}{n^2 \omega_0^2} \cos{n \pi)} \right) - \frac{1}{n^2 \omega_0^2} \right]$

$\displaystyle a_n = \frac{8}{T^2} \left[\frac{1}{n^2 \omega_0^2} + \frac{T}{2n \omega_0} \sin{(-n \pi)} - \frac{1}{n^2 \omega_0^2} \cos{(-n\pi)} \right] - \frac{8}{T^2} \left[ \frac{T}{2n \omega_0} \sin{(n \pi)} + \frac{1}{n^2 \omega_0^2} \cos{(n \pi)} - \frac{1}{n^2 \omega_0^2} \right]$

$\displaystyle a_n = \frac{8}{T^2} \left[\frac{T^2}{n^2 \cdot 4\pi^2} + \frac{T^2}{2n \cdot 2\pi} \sin{(-n \pi)} - \frac{T^2}{n^2 \cdot 4\pi^2} \cos{(-n\pi)} \right] - \frac{8}{T^2} \left[ \frac{T^2}{2n \cdot 2\pi} \sin{(n \pi)} + \frac{T^2}{n^2 \cdot 4\pi^2} \cos{(n \pi)} - \frac{T^2}{n^2 \cdot 4\pi^2} \right]$

$\displaystyle a_n = \frac{8}{T^2} \left[\frac{T^2}{4n^2\pi^2} + \frac{T^2}{4\pi n} \sin{(-n \pi)} - \frac{T^2}{4 n^2 \pi^2} \cos{(-n\pi)} \right] - \frac{8}{T^2} \left[ \frac{T^2}{4n \pi} \sin{(n \pi)} + \frac{T^2}{4 \pi^2 n^2} \cos{(n \pi)} - \frac{T^2}{4 \pi^2 n^2} \right]$

$\displaystyle a_n = \frac{8}{T^2} \frac{T^2}{4n^2\pi^2} + \frac{8}{T^2} \frac{T^2}{4\pi n} \sin{(-n \pi)} - \frac{8}{T^2} \cdot \frac{T^2}{4 n^2 \pi^2} \cos{(-n\pi)} - \frac{8}{T^2} \cdot \frac{T^2}{4n \pi} \sin{(n \pi)} - \frac{8}{T^2} \cdot \frac{T^2}{4 \pi^2 n^2} \cos{(n \pi)} + \frac{8}{T^2} \cdot \frac{T^2}{4 \pi^2 n^2}$

$\displaystyle a_n = \frac{2}{n^2\pi^2} + \frac{2}{\pi n} \sin{(-n \pi)} - \frac{2}{n^2 \pi^2} \cos{(-n\pi)} - \frac{2}{n \pi} \sin{(n \pi)} - \frac{2}{\pi^2 n^2} \cos{(n \pi)} + \frac{2}{\pi^2 n^2}$

$\displaystyle a_n = \frac{2}{n^2\pi^2} - \frac{2}{\pi n} \sin{(n \pi)} - \frac{2}{n^2 \pi^2} \cos{(n\pi)} - \frac{2}{n \pi} \sin{(n \pi)} - \frac{2}{\pi^2 n^2} \cos{(n \pi)} + \frac{2}{\pi^2 n^2}$

$\displaystyle a_n = \frac{4}{n^2\pi^2} - \frac{4}{\pi n} \sin{(n \pi)} - \frac{4}{n^2 \pi^2} \cos{(n\pi)}$

Si $n=1,3,5,7,\cdots$

$\displaystyle \frac{4}{n^2\pi^2} - \frac{4}{\pi n} \sin{(n \pi)} - \frac{4}{n^2 \pi^2} \cos{(n\pi)} = \frac{4}{n^2\pi^2} - \frac{4}{n^2 \pi^2}(-1)$

$\displaystyle = \frac{4}{n^2\pi^2} + \frac{4}{n^2 \pi^2} = \frac{8}{n^2 \pi^2}$

Si $n=2,4,6,8,\cdots$

$\displaystyle \frac{4}{n^2\pi^2} - \frac{4}{\pi n} \sin{(n \pi)} - \frac{4}{n^2 \pi^2} \cos{(n\pi)} = \frac{4}{n^2\pi^2} - \frac{4}{n^2 \pi^2}(1) = 0$

Por tanto, cuando $n$ es impar, el valor de $a_n$ es

$\displaystyle a_n = \frac{8}{n^2 \pi^2}$

Calculando el valor de $b_n$

$\displaystyle b_n = \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{2}{T} \int_{-T/2}^{0}{\left( \frac{4}{T}t + 1\right) \sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{\left( -\frac{4}{T}t + 1\right)\sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{2}{T} \cdot \frac{4}{T} \int_{-T/2}^{0}{t \sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{-T/2}^{0}{\sin{n \omega_0 t} \, dt} - \frac{2}{T} \cdot \frac{4}{T} \int_{0}^{T/2}{t \sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{\sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{8}{T^2} \int_{-T/2}^{0}{t \sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{-T/2}^{0}{\sin{n \omega_0 t} \, dt} - \frac{8}{T^2} \int_{0}^{T/2}{t \sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{\sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{8}{T^2} \int_{-T/2}^{0}{t \sin{n \omega_0 t} \, dt} - \frac{8}{T^2} \int_{0}^{T/2}{t \sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{-T/2}^{0}{\sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{\sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{8}{T^2} \int_{-T/2}^{0}{t \sin{n \omega_0 t} \, dt} - \frac{8}{T^2} \int_{0}^{T/2}{t \sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{-T/2}^{T/2}{\sin{n \omega_0 t} \, dt}$

De la primera y segunda integral

$\displaystyle \int{t \sin{n \omega_0 t} \, dt}$

se resolverá por el método de integración por partes (donde $u=t$ , $du=dt$ , $dv=\sin{n \omega_0 t}$ y $v=-\frac{1}{n \omega_0}\cos{n \omega_0 t}$ ). Entonces

$\displaystyle \int{t \sin{n \omega_0 t} \, dt} = (t)\left[-\frac{1}{n \omega_0}\cos{n \omega_0 t} \right] - \int{\left( -\frac{1}{n \omega_0}\cos{n \omega_0 t}\right) \, dt}$

$\displaystyle \int{t \sin{n \omega_0 t} \, dt} = -\frac{1}{n \omega_0} t \cos{n \omega_0 t} + \frac{1}{n \omega_0} \int{\cos{n \omega_0 t} \, dt}$

$\displaystyle \int{t \sin{n \omega_0 t} \, dt} = -\frac{1}{n \omega_0} t \cos{n \omega_0 t} + \frac{1}{n^2 \omega_0^2} \sin{n \omega_0 t} + C$

En la tercera integral, por propiedad de ortogonalidad

$\displaystyle \int_{-T/2}^{T/2}{\sin{n \omega_0 t} \, dt} = 0$

Regresando y remplazando la variable $t$ por sus respectivos límites, resulta lo siguiente

$\displaystyle b_n = \frac{8}{T^2} \int_{-T/2}^{0}{t \sin{n \omega_0 t} \, dt} - \frac{8}{T^2} \int_{0}^{T/2}{t \sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{-T/2}^{T/2}{\sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{8}{T^2} \left[ -\frac{1}{n \omega_0} t \cos{n \omega_0 t} + \frac{1}{n^2 \omega_0^2} \sin{n \omega_0 t} + C \right]_{-T/2}^{0} - \frac{8}{T^2} \left[ -\frac{1}{n \omega_0} t \cos{n \omega_0 t} + \frac{1}{n^2 \omega_0^2} \sin{n \omega_0 t} + C \right]_{0}^{T/2} + \frac{2}{T} (0)$

$\displaystyle b_n = \frac{8}{T^2} \left[ -\frac{1}{n \omega_0} (0) \cos{(n \omega_0 (0))} + \frac{1}{n^2 \omega_0^2} \sin{(n \omega_0 (0))} - \left( -\frac{1}{n \omega_0} (-\frac{T}{2}) \cos{(n \omega_0 (-\frac{T}{2}))} + \frac{1}{n^2 \omega_0^2} \sin{(n \omega_0 (-\frac{T}{2}))} \right) \right] - \frac{8}{T^2} \left[ -\frac{1}{n \omega_0} (\frac{T}{2}) \cos{(n \omega_0 (\frac{T}{2}))} + \frac{1}{n^2 \omega_0^2} \sin{(n \omega_0 (\frac{T}{2}))} - \left( -\frac{1}{n \omega_0} (0) \cos{(n \omega_0 (0))} + \frac{1}{n^2 \omega_0^2} \sin{(n \omega_0 (0))} \right) \right] + 0$

$\displaystyle b_n = \frac{8}{T^2} \left[- \left( \frac{T}{n \cdot 2\pi } (\frac{T}{2})\cos{(n \frac{2\pi}{T} (-\frac{T}{2}))} + \frac{T^2}{n^2 \cdot 4 \pi^2} \sin{(n (\frac{2\pi}{T}) (-\frac{T}{2}))} \right) \right] - \frac{8}{T^2} \left[ -\frac{T}{n \cdot 2\pi} (\frac{T}{2}) \cos{(n (\frac{2\pi}{T}) (\frac{T}{2}))} + \frac{T^2}{n^2 4 \pi^2} \sin{(n (\frac{2\pi}{T}) (\frac{T}{2}))} - 0 \right]$

$\displaystyle b_n = \frac{8}{T^2} \left[- \left( \frac{T^2}{4 \pi n} \cos{(-n \pi)} + \frac{T^2}{4 n^2 \pi^2} \sin{(-n \pi)} \right) \right] - \frac{8}{T^2} \left[ -\frac{T^2}{4n \pi} \cos{(n \pi)} + \frac{T^2}{4 n^2 \pi^2} \sin{(n \pi)} \right]$

$\displaystyle b_n = - \frac{8}{T^2} \frac{T^2}{4 \pi n} \cos{(-n \pi)} + \frac{8}{T^2} \frac{T^2}{4 n^2 \pi^2} \sin{(-n \pi)} + \frac{8}{T^2}\frac{T^2}{4n \pi} \cos{(n \pi)} - \frac{8}{T^2} \frac{T^2}{4 n^2 \pi^2} \sin{(n \pi)}$

$\displaystyle b_n = - \frac{2}{\pi n} \cos{(-n \pi)} + \frac{2}{n^2 \pi^2} \sin{(-n \pi)} + \frac{2}{n \pi} \cos{(n \pi)} - \frac{2}{n^2 \pi^2} \sin{(n \pi)}$

$\displaystyle b_n = - \frac{2}{\pi n} \cos{(n \pi)} - \frac{2}{n^2 \pi^2} \sin{(n \pi)} + \frac{2}{n \pi} \cos{(n \pi)} - \frac{2}{n^2 \pi^2} \sin{(n \pi)}$

$b_n = 0$

Regresando y sustituyendo los coeficientes de Fourier en la serie de Fourier, el resultado final es

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{\omega_0 t}+b_n \sin{\omega_0 t})}$

$\displaystyle f(t) = \frac{1}{2} (0) + \sum_{n=impar}^{\infty}{(\frac{8}{n^2 \pi^2} \cos{\omega_0 t} + (0) \sin{\omega_0 t})} = \sum_{n=impar}^{\infty}{(\frac{8}{n^2 \pi^2} \cos{\omega_0 t})}$

$\displaystyle \therefore f(t) = \frac{8}{\pi^2} \sum_{n=impar}^{\infty}{ \frac{1}{n^2} \cos{\omega_0 t}}$

Problema 3. Encontrar la serie de Fourier para la función $f(t)$ definida por

$\displaystyle f(t) = \left\{ \begin{matrix} 0 \, , \quad \quad \quad \quad -\frac{T}{2} < t < 0 \\ A \sin{\omega_0 t}, \, \quad \quad 0 < t < \frac{T}{2} \end{matrix} \right.$

y $f(t+T) = f(t)$ , $\omega_0 = \frac{2\pi}{T}$ .

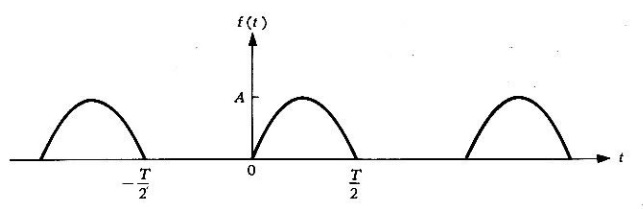
Solución. Recordando la serie de Fourier

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{\omega_0 t}+b_n \sin{\omega_0 t})}$

Se calcula el coeficiente $a_0$

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \, dt}$

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{0}{0 \, dt} + \frac{2}{T} \int_{0}^{T/2}{A \sin{\omega_0 t} \, dt}$

$\displaystyle a_0 = A \cdot \frac{2}{T} \int_{0}^{T/2}{\sin{\omega_0 t} \, dt} = \frac{2A}{T} \int_{0}^{T/2}{\sin{\omega_0 t} \, dt}$

$\displaystyle a_0 = \left[- \frac{2A}{T \omega_0} \cos{\omega_0 t} \right]_{0}^{T/2} = \left[- \frac{2A}{T \omega_0} \cos{(\omega_0 \cdot \frac{T}{2})} \right] - \left[- \frac{2A}{T \omega_0} \cos{(\omega_0 \cdot 0)} \right]$

$\displaystyle a_0 = \left[- \frac{2A}{T \cdot \frac{2\pi}{T}} \cos{(\frac{2\pi}{T} \cdot \frac{T}{2})} \right] - \left[- \frac{2A}{T \cdot \frac{2\pi}{T}} \cos{(0)} \right]$

$\displaystyle a_0 = \left[- \frac{A}{\pi} \cos{\pi} \right] - \left[- \frac{A}{\pi} \cos{0} \right] = \left[- \frac{2A}{\pi} (-1) \right] - \left[- \frac{2A}{\pi} (1) \right]$

$\displaystyle a_0 = \left(\frac{A}{\pi} \right) - \left(- \frac{A}{\pi} \right) = \frac{A}{\pi} + \frac{A}{\pi} = \frac{2A}{\pi}$

$\displaystyle a_0 = \frac{2A}{\pi}$

Calculando $a_n$ , resulta

$\displaystyle a_n = \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \frac{2}{T} \int_{-T/2}^{0}{0 \cdot \cos{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{A \sin{\omega_0 t} \cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \frac{2A}{T} \int_{0}^{T/2}{\sin{\omega_0 t} \cos{n \omega_0 t} \, dt}$

Si $n=1$ , el integrando tiene la siguiente forma

$\displaystyle a_1 = \frac{2A}{T} \int_{0}^{T/2}{\sin{\omega_0 t} \cos{\omega_0 t} \, dt}$

$\displaystyle a_1 = \frac{2A}{T} \left[ \frac{1}{\omega_0} \sin^{2}{\omega_0 t} \right]_{0}^{T/2} = \frac{2A}{T}\left\{ \left[ \frac{1}{\omega_0} \sin^{2}{\omega_0 (\frac{T}{2})} \right] - \left[ \frac{1}{\omega_0} \sin^{2}{\omega_0 (0)} \right] \right\}$

$\displaystyle a_1 = \frac{2A}{T}\left\{ \left[ \frac{1}{\frac{2\pi}{T}} \sin^{2}{(\frac{2\pi}{T}) (\frac{T}{2})} \right] - 0 \right\} = \frac{2A}{T}\left( \frac{T}{2\pi} \sin^{2}{\pi} \right) = 0$

Si $n=2, 3, 4, \cdots$ , el integrando tiene la siguiente forma

$\displaystyle a_n = \frac{2A}{T} \int_{0}^{T/2}{\sin{\omega_0 t} \cos{n \omega_0 t} \, dt}$

Esta integral se resuelve por integración de productos de funciones seno y coseno con diferentes argumentos en la misma variable. Se observa que esta integral de la forma $\displaystyle \int{\sin{mu} \cos{nu} \, du}$ , donde $m=\omega_0$ y $n=\omega_0 n$ , entonces

$\displaystyle \int{\sin{\omega_0 t} \cos{n \omega_0 t} \, dt} = -\frac{1}{2(\omega_0 + n \omega_0)} \cos{(\omega_0 + n\omega_0)t} - \frac{1}{2(\omega_0 + n \omega_0 )}\cos{(\omega_0 - n \omega_0)t}$

$\displaystyle = -\frac{1}{2\omega_0(1 + n)} \cos{\omega_0 (1 + n)t} - \frac{1}{2\omega_0 (1 + n)} \cos{\omega_0(1 - n)t} + C$

Remplazando la variable « $t$ » por sus respectivos límites, resulta lo siguiente

$\displaystyle a_n = \frac{2A}{T} \int_{0}^{T/2}{\sin{\omega_0 t} \cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \frac{2A}{T} \left\{\left[ -\frac{1}{2\omega_0(1 + n)} \cos{\omega_0 (1 + n)t} - \frac{1}{2\omega_0 (1 - n)} \cos{\omega_0(1 - n)t} \right]_{0}^{T/2} \right\}$

$\displaystyle a_n = \frac{2A}{T} \left\{ \left[ -\frac{1}{2\omega_0(1 + n)} \cos{\omega_0 (1 + n)(\frac{T}{2})} - \frac{1}{2\omega_0 (1 - n)} \cos{\omega_0(1 - n)(\frac{T}{2})} \right] - \left[ -\frac{1}{2\omega_0(1 + n)} \cos{\omega_0 (1 + n)(0)} - \frac{1}{2\omega_0 (1 - n)} \cos{\omega_0(1 - n)(0)} \right] \right\}$

$\displaystyle a_n = \frac{2A}{T}\left\{ \left[ -\frac{1}{2(\frac{2\pi}{T})(1 + n)} \cos{(\frac{2\pi}{T}) (1 + n)(\frac{T}{2})} - \frac{1}{2 (\frac{2\pi}{T}) (1 - n)} \cos{(\frac{2\pi}{T})(1 - n)(\frac{T}{2})} \right] - \left[ -\frac{1}{2 (\frac{2\pi}{T}) (1 + n)} \cos{0} - \frac{1}{2 (\frac{2\pi}{T})(1 - n)} \cos{0} \right] \right\}$

$\displaystyle a_n = \frac{2A}{T} \left\{ \left[ -\frac{T}{4\pi (1 + n)} \cos{\pi(1 + n)} - \frac{T}{4 \pi (1 - n)} \cos{\pi (1 - n)} \right] - \left[ -\frac{T}{4 \pi (1 + n)} (1) - \frac{T}{4 \pi (1 - n)}(1) \right] \right\}$

$\displaystyle a_n = \frac{2A}{T}\left[ -\frac{T}{4\pi (1 + n)} \cos{\pi(1 + n)} - \frac{T}{4 \pi (1 - n)} \cos{\pi (1 - n)} + \frac{T}{4 \pi (1 + n)} + \frac{T}{4 \pi (1 - n)} \right]$

$\displaystyle a_n = \frac{2A}{T} \cdot \frac{T}{4\pi} \left[ -\frac{1}{1 + n} \cos{\pi(1 + n)} - \frac{1}{1 - n} \cos{\pi (1 - n)} + \frac{1}{1 + n} + \frac{1}{1 - n} \right]$

$\displaystyle a_n = \frac{A}{2\pi} \left[ -\frac{1}{1 + n} \cos{\pi(1 + n)} - \frac{1}{1 - n} \cos{\pi (1 - n)} + \frac{2}{(1 + n)(1 - n)} \right]$

$\displaystyle a_n = \frac{A}{2\pi} \left[ \frac{2}{(1 + n)(1 - n)} -\frac{1}{1 + n} \cos{\pi(1 + n)} - \frac{1}{1 - n} \cos{\pi (1 - n)} \right]$

$\displaystyle a_n = \frac{A}{2\pi} \cdot \frac{2}{(1 + n)(1 - n)} - \frac{A}{2\pi} \cdot \frac{1}{1 + n} \cos{\pi(1 + n)} - \frac{A}{2\pi} \cdot \frac{1}{1 - n} \cos{\pi (1 - n)}$

$\displaystyle a_n = \frac{A}{\pi(1 + n)(1 - n)} - \frac{A}{2\pi(1 + n)} \cos{\pi(1 + n)} - \frac{A}{2\pi (1 - n)} \cos{\pi (1 - n)}$

Si $n=2,4,6, \cdots$

$\displaystyle a_n = \frac{A}{\pi(1 + n)(1 - n)} - \frac{A}{2\pi(1 + n)} (-1) - \frac{A}{2\pi (1 - n)} (-1)$

$\displaystyle a_n = \frac{A}{\pi(1 + n)(1 - n)} + \frac{A}{2\pi(1 + n)} + \frac{A}{2\pi (1 - n)}$

$\displaystyle a_n = \frac{A}{\pi(1 + n)(1 - n)} + \frac{A}{\pi(1 + n)(1- n)} = \frac{2A}{\pi(1 + n)(1 - n)}$

Si $n=3,5,7, \cdots$

$\displaystyle a_n = \frac{A}{\pi(1 + n)(1 - n)} - \frac{A}{2\pi(1 + n)} (1) - \frac{A}{2\pi (1 - n)} (1)$

$\displaystyle a_n = \frac{A}{\pi(1 + n)(1 - n)} - \frac{A}{2\pi(1 + n)} - \frac{A}{2\pi (1 - n)}$

$\displaystyle a_n = \frac{A}{\pi(1 + n)(1 - n)} - \frac{A}{\pi(1 + n)(1- n)} = 0$

Finalmente

$\displaystyle a_n = \frac{2A}{\pi(1 + n)(1 - n)}$

Cuando $n=2,4,6, \cdots$

Y calculando $b_n$

$\displaystyle b_n = \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{2}{T} \int_{-T/2}^{0}{(0) \sin{n \omega_0 t} \, dt} + \frac{2}{T} \int_{0}^{T/2}{A \sin{\omega_0 t} \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{2A}{T} \int_{0}^{T/2}{\sin{\omega_0 t} \sin{n \omega_0 t} \, dt}$

Si $n=1$ , el integrando tiene la siguiente forma

$\displaystyle b_1 = \frac{2A}{T} \int_{0}^{T/2}{\sin{\omega_0 t} \sin{\omega_0 t} \, dt}$

$\displaystyle b_1 = \frac{2A}{T} \int_{0}^{T/2}{\sin^2{\omega_0 t} \, dt} = \frac{2}{T} \int_{0}^{T/2}{\left(\frac{1}{2} - \frac{1}{2}\cos{2\omega_0 t} \right) \, dt}$

$\displaystyle b_1 = \frac{2A}{T} \left[\frac{1}{2} t - \frac{1}{4 \omega_0} \sin{2\omega_0 t} \right]_{0}^{T/2} = \frac{2A}{T} \left\{ \left[\frac{1}{2} (\frac{T}{2}) - \frac{1}{4 \omega_0} \sin{2\omega_0 (\frac{T}{2})} \right] - \left[\frac{1}{2} (0) - \frac{1}{4 \omega_0} \sin{2\omega_0 (0)} \right] \right\}$

$\displaystyle b_1 = \frac{2A}{T} \left\{ \left[\frac{T}{4} - \frac{1}{4 \omega_0} \sin{\omega_0 T} \right] - 0 \right\} = \frac{2A}{T} \left[\frac{T}{4} - \frac{1}{4 (\frac{2\pi}{T})} \sin{\frac{2\pi}{T} T} \right]$

$\displaystyle b_1 = \frac{2A}{T} \left(\frac{T}{4} - \frac{T}{8 \pi} \sin{2\pi} \right) = \frac{A}{2} - \frac{A}{4 \pi} \sin{2\pi} = \frac{A}{2}$

Si $n=2, 3, 4, \cdots$ , el integrando tiene la siguiente forma

$\displaystyle b_n = \frac{2A}{T} \int_{0}^{T/2}{\sin{\omega_0 t} \sin{n \omega_0 t} \, dt}$

Esta integral se resuelve por integración de productos de funciones seno y coseno con diferentes argumentos en la misma variable. Se observa que esta integral de la forma $\displaystyle \int{\sin{mu} \sin{nu} \, du}$ , donde $m=\omega_0$ y $n=n \omega_0$ , entonces

$\displaystyle \int{\sin{\omega_0 t} \sin{n \omega_0 t} \, dt} = -\frac{1}{2(\omega_0 + n \omega_0)} \sin{(\omega_0 + n \omega_0)t} + \frac{1}{2(\omega_0 - n \omega_0)} \sin{(\omega_0 - n \omega_0)t}$

$\displaystyle = -\frac{1}{2\omega_0 (1 + n)} \sin{\omega_0(1 + n)t} + \frac{1}{2\omega_0(1 - n)} \sin{\omega_0(1 - n)t} + C$

Remplazando la variable « $t$ » por sus respectivos límites, resulta lo siguiente

$\displaystyle = \frac{2A}{T} \int_{0}^{T/2}{\sin{\omega_0 t} \sin{n \omega_0 t} \, dt}$

$\displaystyle = \frac{2A}{T} \left[-\frac{1}{2\omega_0 (1 + n)} \sin{\omega_0(1 + n)t} + \frac{1}{2\omega_0(1 - n)} \sin{\omega_0(1 - n)t} \right]_{0}^{T/2}$

$\displaystyle = \frac{2A}{T} \left\{\left[-\frac{1}{2\omega_0 (1 + n)} \sin{\omega_0(1 + n)(\frac{T}{2})} + \frac{1}{2\omega_0(1 - n)} \sin{\omega_0(1 - n)(\frac{T}{2})} \right] - \left[-\frac{1}{2\omega_0 (1 + n)} \sin{\omega_0(1 + n)(0)} + \frac{1}{2\omega_0(1 - n)} \sin{\omega_0(1 - n)(0)} \right] \right\}$

$\displaystyle = \frac{2A}{T} \left\{\left[-\frac{1}{2 (\frac{2\pi}{T}) (1 + n)} \sin{(\frac{2\pi}{T})(1 + n)(\frac{T}{2})} + \frac{1}{2 (\frac{2\pi}{T}) (1 - n)} \sin{(\frac{2\pi}{T})(1 - n)(\frac{T}{2})} \right] - (-0 + 0) \right\}$

$\displaystyle = \frac{2A}{T} \left[-\frac{T}{4 \pi (1 + n)} \sin{\pi (1 + n)} + \frac{T}{4 \pi (1 - n)} \sin{\pi (1 - n)} \right]$

$\displaystyle = -\frac{A}{2 \pi (1 + n)} \sin{\pi (1 + n)} + \frac{A}{2 \pi (1 - n)} \sin{\pi (1 - n)}$

Si $n=2,4,6, \cdots$

$\displaystyle b_n = -\frac{A}{2 \pi (1 + n)} \sin{\pi (1 + n)} + \frac{A}{2 \pi (1 - n)} \sin{\pi (1 - n)}$

$\displaystyle = -\frac{A}{2 \pi (1 + n)} (0) + \frac{A}{2 \pi (1 - n)} (0) = 0$

Si $n = 3,5,7 \cdots$

$\displaystyle b_n = -\frac{A}{2 \pi (1 + n)} \sin{\pi (1 + n)} + \frac{A}{2 \pi (1 - n)} \sin{\pi (1 - n)}$

$\displaystyle b_n = -\frac{A}{2 \pi (1 + n)} (0) + \frac{A}{2 \pi (1 - n)} (0) = 0$

Finalmente

$b_n = 0$

Regresando y sustituyendo los valores de los coeficientes $a_0$ , $a_n$ y $b_n$ , se tiene el resultado final

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{\omega_0 t}+b_n \sin{\omega_0 t})}$

$\displaystyle f(t) = \frac{1}{2} a_0 + \left(a_1 \cos{\omega_0 t}+b_1 \sin{\omega_0 t}\right) + \sum_{n=2}^{\infty}{(a_n \cos{\omega_0 t}+b_n \sin{\omega_0 t})}$

$\displaystyle f(t) = \frac{1}{2} \cdot \frac{2A}{\pi} + \left[ 0 \cos{\omega_0 t} + \frac{A}{2} \sin{\omega_0 t} \right] + \sum_{n=par}^{\infty}{\left[\frac{2A}{\pi (1+n)(1-n)} \cos{\omega_0 t} + (0) \sin{\omega_0 t} \right]}$

$\displaystyle \therefore f(t) = \frac{A}{\pi} + \frac{A}{2} \sin{\omega_0 t} + \sum_{n=par}^{\infty}{\frac{2A}{\pi (1+n)(1-n)} \cos{\omega_0 t}}$

Problema 4. Desarrollar la función $\sin^5{t}$ en serie de Fourier.

Solución. Utilizando la siguiente identidad

$\displaystyle \sin{t} = \frac{e^{jn t} - e^{-jn t}}{2j}$

Entonces (observando que $n=1$ )

$\displaystyle \sin^5{t} = (\sin{t})^5 = \left( \frac{e^{j t} - e^{-j t}}{2j} \right)^5$

$\displaystyle = \frac{ \left(e^{j t} - e^{-j t} \right)^5}{(2j)^5} = \frac{(e^{j t})^5 + 5 (e^{j t})^4 (-e^{-j t}) + 10 (e^{j t})^3 (-e^{-j t})^2 + 10(e^{j t})^2(-e^{-j t})^3 + 5(e^{j t})(-e^{-j t})^4 + (-e^{-j t})^5}{32j}$

$\displaystyle = \frac{e^{5j t} + 5 (e^{4j t}) (-e^{-j t}) + 10 (e^{3j t}) (e^{-2j t}) + 10(e^{2j t})(-e^{-3j t}) + 5(e^{j t})(e^{-4j t}) + (-e^{-5j t})}{32j}$

$\displaystyle = \frac{e^{5j t} - 5 e^{(4j t - jt)} + 10 e^{(3j t-2j t)} - 10 e^{(2j t-3j t)} + 5 e^{(j t-4j t)} - e^{-5j t}}{32j}$

$\displaystyle = \frac{e^{5j t} - 5 e^{3j t} + 10 e^{j t} - 10 e^{-j t} + 5 e^{-3j t} - e^{-5j t}}{32j}$

$\displaystyle = \frac{e^{5j t} - e^{-5j t} - 5 e^{3j t} + 5 e^{-3j t} + 10 e^{j t} - 10 e^{-j t}}{32j}$

$\displaystyle = \frac{e^{5j t} - e^{-5j t} - 5 (e^{3j t} - e^{-3j t}) + 10 (e^{j t} - e^{-j t})}{32j}$

$\displaystyle = \frac{e^{5j t} - e^{-5j t}}{32j} + \frac{(- 5) (e^{3j t} - e^{-3j t})}{32j} + \frac{(10) (e^{j t} - e^{-j t})}{32j}$

$\displaystyle = \frac{e^{5j t} - e^{-5j t}}{(16)(2j)} + \frac{(- 5) (e^{3j t} - e^{-3j t})}{(16)(2j)} + \frac{(10) (e^{j t} - e^{-j t})}{(16)(2j)}$

$\displaystyle = \frac{1}{16} \left(\frac{e^{5j t} - e^{-5j t}}{2j} \right) + \frac{(- 5)}{16} \left( \frac{e^{3j t} - e^{-3j t}}{2j} \right) + \frac{10}{16} \left(\frac{e^{j t} - e^{-j t}}{2j} \right)$

$\displaystyle = \frac{1}{16} \sin{5 t} - \frac{5}{16}\sin{3t} + \frac{10}{16} \sin{t} = \frac{1}{16} \sin{5 t} - \frac{5}{16}\sin{3t} + \frac{5}{8} \sin{t}$

Finalmente

$\displaystyle \therefore f(t) = \frac{1}{16} \sin{5 t} - \frac{5}{16}\sin{3t} + \frac{5}{8} \sin{t}$

O también

$\displaystyle \therefore f(t) = \frac{5}{8} \sin{t} - \frac{5}{16}\sin{3t} + \frac{1}{16} \sin{5 t}$

Y se concluye que la función $f(t)$ al ser expresado como serie de Fourier, solo consta de tres términos.

Determinando la serie de Fourier de una función “f(t)”. Fourier.

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Determinando la serie de Fourier de una función “f(t)”. Fourier.

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta