Coeficientes de Fourier de ondas simétricas. Fourier.

Teoremas

Teorema 1. Si $f(t)$ es una función periódica par con período $T$ , la serie de Fourier consta de una constante y de términos del coseno solamente, es decir,

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{a_n \cos{n\omega_0 t}}$

donde

$\displaystyle \omega_0 = \frac{2\pi}{T}$

$\displaystyle a_n = \frac{4}{T} \int_{0}^{T/2}{f(t) \cos{n \omega_0 t} \, dt}$

Teorema 2. Si $f(t)$ es una función periódica impar con período $T$ , la parte inferior de la serie de Fourier consta de términos del seno solamente, es decir,

$\displaystyle f(t) = \sum_{n=1}^{\infty}{b_n \sin{n \omega_0 t}}$

donde

$\displaystyle \omega_0 = \frac{2\pi}{T}$

$\displaystyle b_n = \frac{4}{T} \int_{0}^{T/2}{f(t) \sin{n \omega_0 t} \, dt}$

Teorema 3. La serie de Fourier de cualquier función periódica $f(t)$ que tiene simetría de media onda, contiene solamente armónicas impares.

$\displaystyle a_n = \left\{ \begin{matrix} 0 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad para \, n \, par \\ \frac{4}{T} \int_{0}^{T/2}{f(t) \cos{n \omega_0 t} \, dt} \quad \quad para \, n \, impar \end{matrix} \right.$

$\displaystyle b_n = \left\{ \begin{matrix} 0 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad para \, n \, par \\ \frac{4}{T} \int_{0}^{T/2}{f(t) \sin{n \omega_0 t} \, dt} \quad \quad para \, n \, impar \end{matrix} \right.$

Teorema 4. La serie de Fourier de cualquier función periódica $f(t)$ que tiene simetría de cuarto de onda par, consta solamente de armónicos impares términos del coseno, es decir,

$\displaystyle f(t) = \sum_{n=1}^{\infty}{a_{2n-1} \cos{(2n-1) \omega_0 t}}$

donde

$\displaystyle \omega_0 = \frac{2\pi}{T}$

$\displaystyle a_{2n-1} = \frac{8}{T} \int_{0}^{T/4}{f(t) \cos{(2n-1) \omega_0 t} \, dt}$

Teorema 5. La serie de Fourier de cualquier función periódica $f(t)$ que tiene simetría de cuarto de onda impar, consta solamente de armónicos impares de términos del seno, es decir,

$\displaystyle f(t) = \sum_{n=1}^{\infty}{b_{2n-1} \sin{(2n-1) \omega_0 t}}$

donde

$\displaystyle \omega_0 = \frac{2\pi}{T}$

$\displaystyle b_{2n-1} = \frac{8}{T} \int_{0}^{T/4}{f(t) \sin{(2n-1) \omega_0 t} \, dt}$

Problemas resueltos

Problema 1. Encontrar la serie de Fourier de la siguiente onda cuadrada (figura 1).

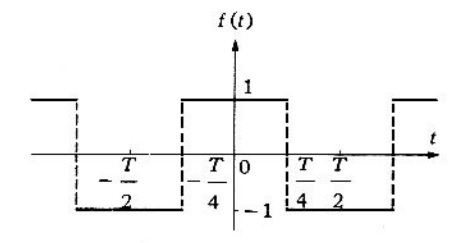
forma de onda del problema 1 — Figura 1. Forma de onda del problema 1.

Solución. En la figura se observa que

$f(-t) = f(t)$ y $\displaystyle f \left(t + \frac{1}{2} T \right) = - f(t)$

Y esto quiere decir que la función $f(t)$ tiene simetría de cuarto de onda par. Por lo que, la serie de Fourier esperado es

$f(t) = \displaystyle \sum_{n=1}^{\infty}{a_{2n-1} \cos{(2n-1) \omega_0 t}}$

Calculando $a_{2n-1}$

$\displaystyle a_{2n-1} = \frac{8}{T} \int_{0}^{T/4}{f(t) \cos{(2n-1) \omega_0 t} \, dt}$

$\displaystyle a_{2n-1} = \frac{8}{T} \int_{0}^{T/4}{(1) \cdot \cos{(2n-1) \omega_0 t} \, dt}$

$\displaystyle a_{2n-1} = \frac{8}{T} \int_{0}^{T/4}{\cos{(2n-1) \omega_0 t} \, dt}$

$\displaystyle a_{2n-1} = \frac{8}{T} \left[ \frac{1}{(2n-1) \omega_0} \sin{(2n-1) \omega_0 t} + C \right]_{0}^{T/4}$

$\displaystyle a_{2n-1} = \frac{8}{T} \left[ \frac{1}{(2n-1) \omega_0} \sin{(2n-1) \omega_0 (\frac{T}{2})} - \frac{1}{(2n-1) \omega_0} \sin{(2n-1) \omega_0 (0)} \right]$

$\displaystyle a_{2n-1} = \frac{8}{T} \left[ \frac{1}{(2n-1) \omega_0} \sin{(2n-1) (\frac{2\pi}{T}) (\frac{T}{4})} - \frac{1}{(2n-1) \omega_0} \sin{(0)} \right]$

$\displaystyle a_{2n-1} = \frac{8}{T} \left[ \frac{1}{(2n-1) \omega_0} \sin{(2n-1) \frac{\pi}{2}} \right] = \frac{8}{T} \left[ \frac{1}{(2n-1) \frac{2\pi}{T}} \sin{(2n-1) \frac{\pi}{2}} \right]$

$\displaystyle a_{2n-1}= \frac{8}{T} \left[ \frac{T}{2 (2n-1) \pi} \sin{(2n-1) \frac{\pi}{2}} \right] = \frac{4}{(2n-1) \pi} \sin{(2n-1) \frac{\pi}{2}}$

Si $n=1,3,5, \cdots$

$\displaystyle a_{2n-1} = \frac{4}{(2n-1) \pi} \sin{(2n-1) \frac{\pi}{2}}$

$\displaystyle a_{2n-1} = \frac{4}{(2n-1) \pi} (1) = \frac{4}{(2n-1) \pi}$

$\displaystyle a_{2n-1} = \frac{4}{(2n-1) \pi}$

Si $n=2,4,6, \cdots$

$\displaystyle a_{2n-1} = \frac{4}{(2n-1) \pi} \sin{(2n-1) \frac{\pi}{2}}$

$\displaystyle a_{2n-1} = \frac{4}{(2n-1) \pi} (-1) = - \frac{4}{(2n-1) \pi}$

$\displaystyle a_{2n-1} = - \frac{4}{(2n-1) \pi}$

Entonces $a_{2n-1}$ es

$\displaystyle \large a_{2n-1} = \left\{ \begin{matrix} \frac{4}{(2n-1) \pi} \quad , \quad n=1,3,5, \cdots \\ - \frac{4}{(2n-1) \pi} \quad, \quad n =2,4,6, \cdots \end{matrix} \right.$

Regresando, el resultado final es

$\displaystyle f(t) = \sum_{n=1}^{\infty}{a_{2n-1} \cos{(2n-1) \omega_0 t}}$

$\displaystyle f(t) = \sum_{n=1}^{\infty}{\frac{4}{(2n-1) \pi} \sin{(2n-1) \frac{\pi}{2}} \cdot \cos{(2n-1) \omega_0 t}}$

$\displaystyle \therefore f(t) = \frac{4}{\pi} \sum_{n=1}^{\infty}{\left(\frac{1}{2n-1} \right) \sin{(2n-1) \frac{\pi}{2}} \cdot \cos{(2n-1) \omega_0 t}}$

O también

$\displaystyle \therefore f(t) = \frac{4}{\pi} \left[ \sum_{n=impar}^{\infty}{\left( \frac{1}{2n-1} \right) \cos{(2n-1) \omega_0 t}} + \sum_{n=par}^{\infty}{\left( \frac{1}{2n-1} \right) \cos{(2n-1) \omega_0 t}} \right]$

Problema 2. Encontrar la serie de Fourier de la siguiente forma de onda cuadrada (figura 2.)

forma de onda del problema 2 — Figura 2. Forma de onda del problema 2.

Solución. Observando la figura 2.2.2, se tiene lo siguiente

$\displaystyle f(-t) = - f(t)$ y $\displaystyle f \left(t + \frac{1}{2} T \right)$

esto quiere decir que la función $f(t)$ tiene simetría de cuarto de onda impar. La serie de Fourier esperado es

$\displaystyle f(t) = \sum_{n=1}^{\infty}{b_{2n-1} \sin{(2n-1) \omega_0 t}}$

Calculando $b_{2n-1}$

$\displaystyle b_{2n-1} = \frac{8}{T} \int_{0}^{T/4}{f(t) \sin{(2n-1) \omega_0 t} \, dt}$

$\displaystyle b_{2n-1} = \frac{8}{T} \int_{0}^{T/4}{(1) \sin{(2n-1) \omega_0 t} \, dt}$

$\displaystyle b_{2n-1} = \frac{8}{T} \int_{0}^{T/4}{\sin{(2n-1) \omega_0 t} \, dt}$

$\displaystyle b_{2n-1} = \frac{8}{T} \left[- \frac{1}{(2n-1) \omega_0} \cos{(2n-1) \omega_0 t} + C \right]_{0}^{T/4}$

$\displaystyle b_{2n-1} = \frac{8}{T} \left[- \frac{1}{(2n-1) \omega_0} \cos{(2n-1) \omega_0 (\frac{T}{4})} + \frac{1}{(2n-1) \omega_0} \cos{(2n-1) \omega_0 (0)} \right]$

$\displaystyle b_{2n-1} = \frac{8}{T} \left[- \frac{1}{(2n-1) \frac{2\pi}{T}} \cos{(2n-1) \frac{2\pi}{T} (\frac{T}{4})} + \frac{1}{(2n-1) \frac{2\pi}{T}} \cos{(0)} \right]$

$\displaystyle b_{2n-1} = \frac{8}{T} \left[- \frac{T}{2 (2n-1) \pi} \cos{(2n-1) \frac{\pi}{2}} + \frac{T}{2 (2n-1)\pi} (1) \right]$

$\displaystyle b_{2n-1} = - \frac{4}{(2n-1) \pi} \cos{(2n-1) \frac{\pi}{2}} + \frac{4}{(2n-1)\pi}$

Si $n=1,3,5, \cdots$

$\displaystyle b_{2n-1} = - \frac{4}{(2n-1) \pi} \cos{(2n-1) \frac{\pi}{2}} + \frac{4}{(2n-1)\pi}$

$\displaystyle b_{2n-1} = - \frac{4}{(2n-1) \pi} (0) + \frac{4}{(2n-1)\pi}$

$\displaystyle b_{2n-1} = \frac{4}{(2n-1)\pi}$

Si $n=2,4,6, \cdots$

$\displaystyle b_{2n-1} = - \frac{4}{(2n-1) \pi} \cos{(2n-1) \frac{\pi}{2}} + \frac{4}{(2n-1)\pi}$

$\displaystyle b_{2n-1} = - \frac{4}{(2n-1) \pi} (0) + \frac{4}{(2n-1)\pi}$

$\displaystyle b_{2n-1} = \frac{4}{(2n-1)\pi}$

Entonces $b_{2n-1}$ es

$\displaystyle \large b_{2n-1} = \frac{4}{(2n-1)\pi}$

Regresando, el resultado final es

$\displaystyle f(t) = \sum_{n=1}^{\infty}{b_{2n-1} \sin{(2n-1) \omega_0 t}}$

$\displaystyle f(t) = \sum_{n=1}^{\infty}{\frac{4}{(2n-1)\pi} \cdot \sin{(2n-1) \omega_0 t}}$

$\displaystyle \therefore f(t) = \frac{4}{\pi} \sum_{n=1}^{\infty}{ \left(\frac{1}{2n-1} \right) \sin{(2n-1) \omega_0 t}}$

Problema 3. Encontrar la serie de Fourier de la función $f(t)$ que se muestra en la siguiente figura

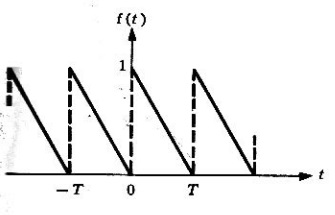
forma de onda del problema 3a — Figura 3. Forma de onda del problema 3.

Solución. La figura presenta una simetría escondida, para ello, se desplazará $1/2$ de la función para tener la siguiente forma

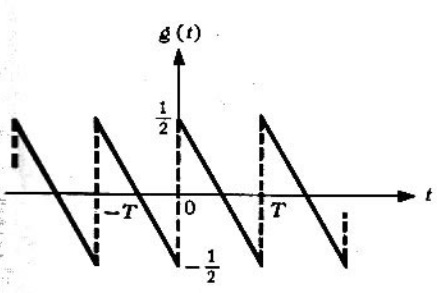
forma de onda del problema 3b — Figura 4. Forma de onda que se ha desplazado 1/2 haciéndolo simétrico en el eje «t».

Y la nueva función a tomar para resolver este problema es $\displaystyle g(t) = f(t) - \frac{1}{2}$ , donde $g(t)$ es una función impar. De $f(t)$ (de la figura 2.2.3), la función es ( $0 < t < T$ )

$\displaystyle f(t) - f(t_1) = \left[ \frac{f(t_2) - f(t_1)}{t_2 - t_1} \right] (t - t_1)$

$\displaystyle f(t) - 1 = \left( \frac{-\frac{1}{2} - \frac{1}{2}}{T - 0} \right) (t - 0)$

$\displaystyle f(t) - 1 = \left(- \frac{1}{T} \right) (t)$

$\displaystyle f(t) - 1 = - \frac{1}{T} t$

$\displaystyle f(t) = 1 - \frac{1}{T} t$

Por lo que $g(t)$ (de la figura 2.2.4) es

$\displaystyle g(t) = f(t) - \frac{1}{2}$

$\displaystyle g(t) = 1 - \frac{1}{T} t - \frac{1}{2}$

$\displaystyle g(t) = \frac{1}{2} - \frac{1}{T} t$

Si $g(t)$ es impar, la serie de Fourier es

$\displaystyle g(t) = \sum_{n=1}^{\infty}{b_n \sin{n \omega_0 t}}$

Calculando $b_n$

$\displaystyle b_n = \frac{4}{T} \int_{0}^{T/2}{g(t) \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{4}{T} \int_{0}^{T/2}{\left(\frac{1}{2} - \frac{1}{T} t \right) \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{4}{T} \int_{0}^{T/2}{\frac{1}{2} \sin{n \omega_0 t} \, dt} + \frac{4}{T} \int_{0}^{T/2}{\left(- \frac{1}{T} t \right) \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{2}{T} \int_{0}^{T/2}{\sin{n \omega_0 t} \, dt} - \frac{4}{T^2} \int_{0}^{T/2}{t \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{1}{n \omega_0} \right) \cos{n \omega_0 t} + C \right]_{0}^{T/2} - \frac{4}{T^2} \left[\left(-\frac{1}{n \omega_0} \right) t \cos{n \omega_0 t} + \left( \frac{1}{n \omega_0} \right)^2 \sin{n \omega_0 t} + C \right]_{0}^{T/2}$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{1}{n \omega_0} \right) \cos{n \omega_0 (\frac{T}{2})} + \left(\frac{1}{n \omega_0} \right) \cos{n \omega_0 (0)} \right] - \frac{4}{T^2} \left[\left(-\frac{1}{n \omega_0} \right) (\frac{T}{2}) \cos{n \omega_0 (\frac{T}{2})} + \left( \frac{1}{n \omega_0} \right)^2 \sin{n \omega_0 (\frac{T}{2})} - \left(-\frac{1}{n \omega_0} \right) (0) \cos{n \omega_0 (0)} - \left( \frac{1}{n \omega_0} \right)^2 \sin{n \omega_0 (0)} \right]$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{1}{n \omega_0} \right) \cos{n \omega_0 (\frac{T}{2})} + \left(\frac{1}{n \omega_0} \right) (1) \right] - \frac{4}{T^2} \left[\left(-\frac{1}{n \omega_0} \right) (\frac{T}{2}) \cos{n \omega_0 (\frac{T}{2})} + \left( \frac{1}{n \omega_0} \right)^2 \sin{n \omega_0 (\frac{T}{2})} - (0) (1) - \left( \frac{1}{n \omega_0} \right)^2 (0) \right]$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{1}{n \omega_0} \right) \cos{n \omega_0 (\frac{T}{2})} + \left(\frac{1}{n \omega_0} \right) \right] - \frac{4}{T^2} \left[\left(-\frac{1}{n \omega_0} \right) (\frac{T}{2}) \cos{n \omega_0 (\frac{T}{2})} + \left( \frac{1}{n \omega_0} \right)^2 \sin{n \omega_0 (\frac{T}{2})} \right]$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{1}{n \left(\frac{2\pi}{T} \right)} \right) \cos{n \left(\frac{2\pi}{T} \right) (\frac{T}{2})} + \left(\frac{1}{n \left(\frac{2\pi}{T} \right)} \right) \right] - \frac{4}{T^2} \left[\left(-\frac{1}{n \left(\frac{2\pi}{T} \right)} \right) (\frac{T}{2}) \cos{n \left(\frac{2\pi}{T} \right) (\frac{T}{2})} + \left( \frac{1}{n \left(\frac{2\pi}{T} \right)} \right)^2 \sin{n \left(\frac{2\pi}{T} \right) (\frac{T}{2})} \right]$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{T}{2 n \pi} \right) \cos{n \pi} + \left(\frac{T}{2n \pi} \right) \right] - \frac{4}{T^2} \left[ \left(- \frac{T^2}{4 n \pi} \right) \cos{n \pi} + \left( \frac{T}{2 n \pi} \right)^2 \sin{n \pi} \right]$

$\displaystyle b_n = \frac{2}{T} \left(- \frac{T}{2 n \pi} \cos{n \pi} + \frac{T}{2n \pi} \right) - \frac{4}{T^2} \left( - \frac{T^2}{4 n \pi} \cos{n \pi} + \frac{T^2}{4 n^2 \pi^2} \sin{n \pi} \right)$