Expansión en serie de Fourier de una función en un intervalo finito. Fourier.

Introducción

Una función $f(t)$ no periódica, definida en cierto intervalo finito $(0, \, \tau)$ , se puede desarrollar en una serie de Fourier, la cual está definida solamente en el intervalo $(0, \, \tau)$ . Es posible desarrollar $f(t)$ en una serie de Fourier con cualquier frecuencia fundamental deseada; demás $f(t)$ se puede representar por una serie de términos del seno o coseno solamente, lo cual se puede hacer construyendo una función periódica adecuada que sea idéntica a $f(t)$ en el intervalo $(, \, \tau)$ , y que satisfaga las condiciones de simetría que conduzcan a la forma deseada de las series de Fourier.

Expansiones de medio corrido

Sea $f(t)$ una función de período $T=2\tau$ . Si $f(t)$ es par, entonces, la serie de Fourier tendrá términos del coseno.

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{a_n \cos{\left(\frac{n \pi}{\tau}t \right)} }$

donde $a_n$ es

$\displaystyle a_n = \frac{2}{\tau} \int_{0}^{\tau}{f(t) \cos{\frac{n\pi}{\tau} t} \, dt}$

Si $f(t)$ es impar, entonces, la serie de Fourier tendrá términos del seno

$\displaystyle f(t) = \sum_{n=1}^{\infty}{b_n \sin{\left( \frac{n \pi}{\tau} \right)}}$

donde $b_n$ es

$\displaystyle b_n = \frac{2}{\tau} \int_{0}^{\tau}{f(t) \sin{\frac{n\pi}{\tau} t} \, dt}$

Estas series de Fourier, ambas representan la misma función $f(t)$ dada, en el intervalo $(0, \, \tau)$ , fuera de este intervalo, la serie de Fourier donde tendrá términos del coseno representará la extensión periódica par de $f(t)$ , con período $T=2\tau$ , y la serie de Fourier donde tendrá solo términos del seno representará la extensión impar de $f(t)$ , con período $T=2\tau$ . Las series que contienen los coeficientes $a_n$ y $b_n$ se denominan expansiones de medio recorrido de la función $f(t)$ dada.

Problemas resueltos

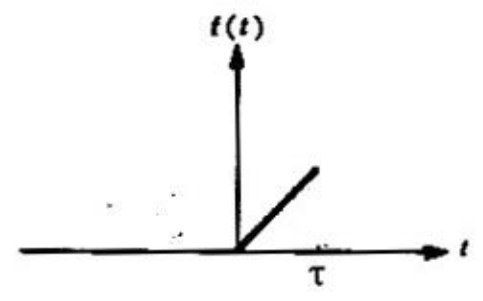
Problema 1. Dada la función (figura 8)

$\displaystyle f(t) = \left\{ \begin{matrix} 0 \quad \text{para} \quad 0 < t < \frac{1}{2} \pi \\1 \quad \text{para} \quad \frac{1}{2} \pi < t < \pi \end{matrix} \right.$

desarrollar $f(t)$ en una serie de Fourier de términos del coseno y trazar la correspondiente extensión periódica de $f(t)$ .

Figura 2.3.2 — *Figura 8. Representación gráfica de la función del problema 1.*

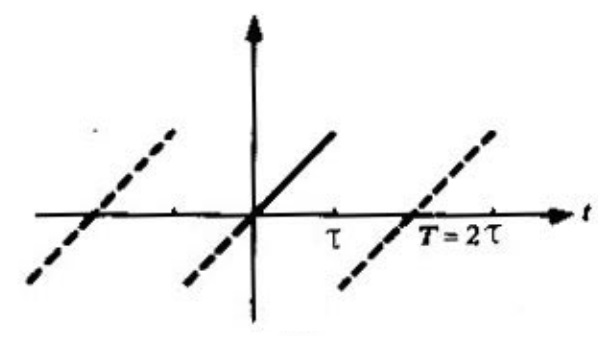
Solución. Se elabora una gráfica que represente la extensión periódica par de $f(t)$ .

Figura 2.3.3 — *Figura 9. Representación gráfica de la extensión periódica par de «f(t)».*

Como $f(t)$ se extiende a una función par, $b_n = 0$ . Cuando $n = 1,2,3,4, \cdots$ , el valor de $a_n$ es

$\displaystyle a_n = \frac{2}{\tau} \int_{0}^{\tau}{f(t) \cos{\frac{n\pi}{\tau} t} \, dt}$

$\displaystyle a_n = \frac{2}{\pi} \int_{0}^{\pi/2}{(0) \cos{\frac{n\pi}{\pi} t} \, dt} + \frac{2}{\pi} \int_{\pi/2}^{\pi}{(1) \cos{\frac{n\pi}{\pi} t} \, dt}$

$\displaystyle a_n = \frac{2}{\pi} \int_{\pi/2}^{\pi}{\cos{n t} \, dt} = \frac{2}{\pi} \left[\frac{1}{n} \sin{nt} +C \right]_{\pi/2}^{\pi}$

$\displaystyle a_n = \frac{2}{\pi} \left[\frac{1}{n} \sin{n \pi} - \frac{1}{n} \sin{n (\frac{\pi}{2})} \right]$

$\displaystyle a_n = \frac{2}{n \pi} \sin{n \pi} - \frac{2}{n \pi} \sin{\frac{n\pi}{2}}$

Si $n =1, 5, 9, \cdots$

$\displaystyle a_n = \frac{2}{n \pi} \sin{n \pi} - \frac{2}{n \pi} \sin{\frac{n\pi}{2}}$

$\displaystyle a_n = \frac{2}{n \pi} (0) - \frac{2}{n \pi} (1)$

$\displaystyle a_n = - \frac{2}{n \pi}$

Si $n = 2, 4, 6, \cdots$

$\displaystyle a_n = \frac{2}{n \pi} \sin{n \pi} - \frac{2}{n \pi} \sin{\frac{n\pi}{2}}$

$\displaystyle a_n = \frac{2}{n \pi} (0) - \frac{2}{n \pi} (0)$

$\displaystyle a_n = 0$

Si $n =3, 7, 11, \cdots$

$\displaystyle a_n = \frac{2}{n \pi} \sin{n \pi} - \frac{2}{n \pi} \sin{\frac{n\pi}{2}}$

$\displaystyle a_n = \frac{2}{n \pi} (0) - \frac{2}{n \pi} (-1)$

$\displaystyle a_n = \frac{2}{n \pi}$

Entonces, $a_n$ es

$\displaystyle \large a_n = \left\{ \begin{matrix} - \frac{2}{n \pi} \quad \quad n=1,5,9, \cdots \\ 0 \quad \quad n=2,4,6,\cdots \\ \frac{2}{n \pi} \quad \quad n=3,7,11, \cdots \end{matrix} \right.$

Cuando $n = 0$ , el valor de $a_n$ es

$\displaystyle a_0 = \frac{2}{\tau} \int_{0}^{\tau}{f(t) \, dt}$

$\displaystyle a_0 = \frac{2}{\pi} \int_{0}^{\pi/2}{(0) \, dt} + \frac{2}{\pi} \int_{\pi/2}^{\pi}{(1) \, dt}$

$\displaystyle a_0 = \frac{2}{\pi} \int_{\pi/2}^{\pi}{dt} = \frac{2}{\pi} \left[t +C \right]_{\pi/2}^{\pi}$

$\displaystyle a_0 = \frac{2}{\pi} \left[\pi - \frac{\pi}{2} \right] = \frac{2}{\pi} \left(\frac{\pi}{2} \right) = 1$

Entonces, $a_0$ es

$a_0 = 1$

Finalmente, la serie de Fourier esperado es

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{a_n \cos{\left(\frac{n \pi}{\tau} t \right)}}$

$\displaystyle f(t) = \frac{1}{2} (1) + \sum_{n=1, 5, 9, \cdots}^{\infty}{(-\frac{2}{n \pi}) \cos{\left(\frac{n \pi}{\pi} t \right)}} + \sum_{n=3, 7, 11, \cdots}^{\infty}{(\frac{2}{n \pi}) \cos{\left(\frac{n \pi}{\pi} t \right)}}$

$\displaystyle \therefore f(t) = \frac{1}{2} - \frac{2}{\pi} \sum_{n=1, 5, 9, \cdots}^{\infty}{\frac{1}{n} \cos{n t}} + \frac{2}{\pi}\sum_{n=3, 7, 11, \cdots}^{\infty}{\frac{1}{n} \cos{n t}}$

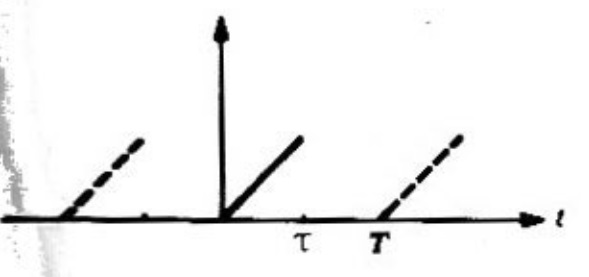
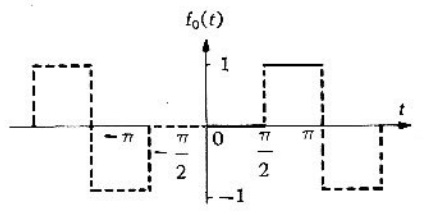
Problema 2. Desarrollar $f(t)$ definida por (figura 10)

$\displaystyle f(t) = \left\{ \begin{matrix} 0 \quad \text{para} \quad 0 < t < \frac{1}{2} \pi \\1 \quad \text{para} \quad \frac{1}{2} \pi < t < \pi \end{matrix} \right.$

en una serie de Fourier expresada en términos del seno y trazar la gráfica correspondiente extensión periódica de $f(t)$ .

Solución. Se elabora una gráfica que represente la extensión periódica impar de $f(t)$ .

Figura 2.3.4 — *Figura 11. Representación gráfica de la extensión periódica impar de «f(t)».*

Como $f(t)$ es una función impar, $a_n = 0$ . El valor de $b_n$ es

$\displaystyle b_n = \frac{2}{\tau} \int_{0}^{\tau}{f(t) \sin{\frac{n\pi}{\tau} t} \, dt}$

$\displaystyle b_n = \frac{2}{\pi} \int_{0}^{\pi}{f(t) \sin{\frac{n\pi}{\pi} t} \, dt}$

$\displaystyle b_n = \frac{2}{\pi} \int_{\pi/2}^{\pi}{f(t) \sin{n t} \, dt}$

$\displaystyle b_n = \frac{2}{\pi} \int_{\pi/2}^{\pi/2}{(0) \sin{n t} \, dt} + \frac{2}{\pi} \int_{\pi/2}^{\pi}{(1) \sin{n t} \, dt}$

$\displaystyle b_n = \frac{2}{\pi} \int_{\pi/2}^{\pi}{\sin{n t} \, dt}$

$\displaystyle b_n = \frac{2}{\pi} \left[- \frac{1}{n} \cos{n t} + C \right]_{\pi/2}^{\pi}$

$\displaystyle b_n = \frac{2}{\pi} \left[- \frac{1}{n} \cos{n \pi} + \frac{1}{n} \cos{n (\frac{\pi}{2})} \right]$

$\displaystyle b_n = \frac{2}{\pi} \left(- \frac{1}{n} \cos{n \pi} + \frac{1}{n} \cos{\frac{n\pi}{2}} \right) = \frac{2}{\pi} \cdot \frac{1}{n} \left(-\cos{n \pi} + \cos{\frac{n\pi}{2}} \right)$

$\displaystyle b_n = \frac{2}{n \pi} \left(-\cos{n \pi} + \cos{\frac{n\pi}{2}} \right)$

Si $n=1,3,5,\cdots$ , $b_n$ es

$\displaystyle b_n = \frac{2}{n \pi} \left(-\cos{n \pi} + \cos{\frac{n\pi}{2}} \right)$

$\displaystyle b_n = \frac{2}{n \pi} \left[-(-1) + (0) \right] = \frac{2}{n \pi} (1)$

$\displaystyle b_n = \frac{2}{n \pi}$

Si $n=2,6,10, \cdots$ , $b_n$ es

$\displaystyle b_n = \frac{2}{n \pi} \left(-\cos{n \pi} + \cos{\frac{n\pi}{2}} \right)$

$\displaystyle b_n = \frac{2}{n \pi} \left[-(1) + (-1) \right] = \frac{2}{n \pi} (-2)$

$\displaystyle b_n = - \frac{4}{n \pi}$

Si $n=4,8,12, \cdots$ , $b_n$ es

$\displaystyle b_n = \frac{2}{n \pi} \left(-\cos{n \pi} + \cos{\frac{n\pi}{2}} \right)$

$\displaystyle b_n = \frac{2}{n \pi} \left[-(1) + (1) \right] = \frac{2}{n \pi} (0)$

$\displaystyle b_n = 0$

Entonces, $b_n$ es

$\displaystyle \large b_n = \left\{ \begin{matrix} \frac{2}{n \pi} \quad \quad n=1,3,5, \cdots \\ - \frac{4}{n \pi} \quad \quad n=2,6,10,\cdots \\ 0 \quad \quad n=4,8,12, \cdots \end{matrix} \right.$

Finalmente, la serie de Fourier esperado es

$\displaystyle f(t) = \sum_{n=1}^{\infty}{b_n \sin{\left(\frac{n \pi}{\tau} t \right)}}$

$\displaystyle f(t) = \sum_{n=1}^{\infty}{b_n \sin{\left(\frac{n \pi}{\pi} t \right)}}$

$\displaystyle f(t) = \sum_{n=1}^{\infty}{b_n \sin{n t}}$

$\displaystyle f(t) = \sum_{n=1,3,5,\cdots}^{\infty}{\frac{2}{n \pi} \sin{n t}} + \sum_{n=2,6,10,\cdots}^{\infty}{(- \frac{4}{n \pi}) \sin{n t}} + \sum_{n=4,8,12,\cdots}^{\infty}{0 \sin{n t}}$

$\displaystyle f(t) = \frac{2}{\pi} \sum_{n=1,3,5,\cdots}^{\infty}{\frac{1}{n} \sin{n t}} - \frac{4}{\pi} \sum_{n=2,6,10,\cdots}^{\infty}{\frac{1}{n} \sin{n t}}$

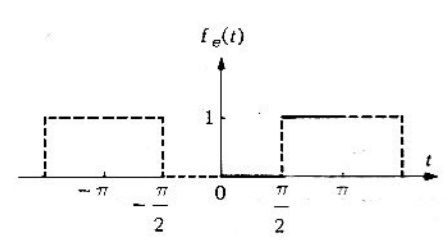
Problema 3. Dada la función (figura 12)

$\displaystyle \large f(t) = \left\{ \begin{matrix} \frac{2k}{l} \quad \quad \quad \quad \text{para} \quad 0 < t < \frac{1}{2} l \\\frac{2k}{l} (l - t) \quad \text{para} \quad \frac{1}{2} l < t < l \end{matrix} \right.$

Figura 2.3.5 — *Figura 12. Representación gráfica de la función del problema 3.*

desarrollar $f(t)$ en una serie de Fourier en términos del seno.

Solución. Se elabora una gráfica que represente la extensión periódica impar de $f(t)$ .

Figura 2.3.6 — *Figura 13. Representación gráfica de la extensión periódica impar de la función «f(t)».*

Como $f(t)$ es una función impar, $a_n = 0$ . El valor de $b_n$ es

$\displaystyle b_n = \frac{2}{\tau} \int_{0}^{\tau}{f(t) \sin{\frac{n\pi}{\tau} t} \, dt}$

$\displaystyle b_n = \frac{2}{l} \int_{0}^{l}{f(t) \sin{\frac{n\pi}{l} t} \, dt}$

$\displaystyle b_n = \frac{2}{l} \int_{0}^{l/2}{\frac{2k}{l} t \sin{\frac{n\pi}{l} t} \, dt} + \frac{2}{l} \int_{l/2}^{l}{\frac{2k}{l} (l - t) \sin{\frac{n\pi}{l} t} \, dt}$

$\displaystyle b_n = \frac{4k}{l^2} \int_{0}^{l/2}{t \sin{\frac{n\pi}{l} t} \, dt} + \frac{4k}{l^2} \int_{l/2}^{l}{(l - t) \sin{\frac{n\pi}{l} t} \, dt}$

$\displaystyle b_n = \frac{4k}{l^2} \left[-\frac{l}{n \pi} t \cos{\frac{n\pi}{l} t} + \left(\frac{l}{n\pi} \right)^2 \sin{\frac{n\pi}{l} t} + C \right]_{0}^{l/2} + \frac{4k}{l^2} \left[-\frac{1}{n \pi} (l - t) \cos{\frac{n\pi}{l} t} - \left(\frac{l}{n \pi} \right)^2 \sin{\frac{n\pi}{l} t} + C \right]_{l/2}^{l}$

$\displaystyle b_n = \frac{4k}{l^2} \left[-\frac{l}{n \pi} \left(\frac{l}{2} \right) \cos{\frac{n\pi}{l} \left(\frac{l}{2} \right)} + \left(\frac{l}{n\pi} \right)^2 \sin{\frac{n\pi}{l} \left(\frac{l}{2} \right)} + \frac{l}{n \pi} (0) \cos{\frac{n\pi}{l} (0)} - \left(\frac{l}{n\pi} \right)^2 \sin{\frac{n\pi}{l} (0)} \right]$

$\displaystyle + \frac{4k}{l^2} \left[-\frac{l}{n \pi} (l - l) \cos{\frac{n\pi}{l} (l)} - \left(\frac{l}{n \pi} \right)^2 \sin{\frac{n\pi}{l} (l)} + \frac{l}{n \pi} \left(l - \frac{l}{2} \right) \cos{\frac{n\pi}{l} \left(\frac{l}{2} \right)} + \left(\frac{l}{n \pi} \right)^2 \sin{\frac{n\pi}{l} \left(\frac{l}{2} \right)} \right]$

$\displaystyle b_n = \frac{4k}{l^2} \left[-\frac{l}{n \pi} \left(\frac{l}{2} \right) \cos{\frac{n\pi}{2}} + \frac{l^2}{n^2\pi^2} \sin{\frac{n\pi}{2}} \right] + \frac{4k}{l^2} \left[-\frac{l}{n \pi} (0) \cos{n\pi} - \frac{l^2}{n^2 \pi^2} \sin{n\pi} + \frac{l}{n \pi} \left(\frac{l}{2} \right) \cos{\frac{n\pi}{2}} + \frac{l^2}{n^2 \pi^2} \sin{\frac{n\pi}{2}} \right]$

$\displaystyle b_n = \frac{4k}{l^2} \left(-\frac{l^2}{2n \pi} \cos{\frac{n\pi}{2}} + \frac{l^2}{n^2\pi^2} \sin{\frac{n\pi}{2}} \right) + \frac{4k}{l^2} \left(- \frac{l^2}{n^2 \pi^2} \sin{n\pi} + \frac{l^2}{2n \pi} \cos{\frac{n\pi}{2}} + \frac{l^2}{n^2 \pi^2} \sin{\frac{n\pi}{2}} \right)$

$\displaystyle b_n = - \frac{2k}{n \pi} \cos{\frac{n\pi}{2}} + \frac{4k}{n^2\pi^2} \sin{\frac{n\pi}{2}} - \frac{4k}{n^2 \pi^2} \sin{n\pi} + \frac{2k}{n \pi} \cos{\frac{n\pi}{2}} + \frac{4k}{n^2 \pi^2} \sin{\frac{n\pi}{2}}$

$\displaystyle b_n = \frac{8k}{n^2\pi^2} \sin{\frac{n\pi}{2}} - \frac{4k}{n^2 \pi^2} \sin{n\pi}$

Si $n=1,5,9, \cdots$ , $b_n$ es

$\displaystyle b_n = \frac{8k}{n^2\pi^2} \sin{\frac{n\pi}{2}} - \frac{4k}{n^2 \pi^2} \sin{n\pi}$

$\displaystyle b_n = \frac{8k}{n^2\pi^2} (1) - \frac{4k}{n^2 \pi^2} (0)$

$\displaystyle b_n = \frac{8k}{n^2\pi^2}$

Si $n=3,7,11, \cdots$ , $b_n$ es

$\displaystyle b_n = \frac{8k}{n^2\pi^2} \sin{\frac{n\pi}{2}} - \frac{4k}{n^2 \pi^2} \sin{n\pi}$

$\displaystyle b_n = \frac{8k}{n^2\pi^2} (-1) - \frac{4k}{n^2 \pi^2} (0)$

$\displaystyle b_n = - \frac{8k}{n^2\pi^2}$

Si $n=2,4,6, \cdots$ , $b_n$ es

$\displaystyle b_n = \frac{8k}{n^2\pi^2} \sin{\frac{n\pi}{2}} - \frac{4k}{n^2 \pi^2} \sin{n\pi}$

$\displaystyle b_n = \frac{8k}{n^2\pi^2} (0) - \frac{4k}{n^2 \pi^2} (0)$

$\displaystyle b_n = 0$

Entonces, el valor de $b_n$ es

$\displaystyle \large b_n = \left\{ \begin{matrix} \frac{8k}{n^2 \pi^2} \quad \quad n=1,5,9, \cdots \\ - \frac{8k}{n^2 \pi^2} \quad \quad n=3,7,11,\cdots \\ 0 \quad \quad n=2,4,6, \cdots \end{matrix} \right.$

Finalmente, la serie de Fourier esperado es

$\displaystyle f(t) = \sum_{n=1}^{\infty}{b_n \sin{\left(\frac{n \pi}{\tau} t \right)}}$

$\displaystyle f(t) = \sum_{n=1}^{\infty}{b_n \sin{\left(\frac{n \pi}{\pi} t \right)}}$

$\displaystyle f(t) = \sum_{n=1}^{\infty}{b_n \sin{n t}}$

$\displaystyle f(t) = \sum_{n=1,5,9,\cdots }^{\infty}{\frac{8k}{n^2 \pi^2} \sin{n t}} + \sum_{n=3,7,11,\cdots}^{\infty}{\left(- \frac{8k}{n^2 \pi^2} \right) \sin{n t}} + \sum_{n=2,4,6,\cdots}^{\infty}{0 \sin{n t}}$

$\displaystyle \therefore f(t) = \frac{8k}{\pi} \sum_{n=1,5,9,\cdots }^{\infty}{\frac{1}{n^2} \sin{n t}} - \frac{8k}{\pi} \sum_{n=3,7,11,\cdots}^{\infty}{\frac{1}{n^2} \sin{n t}}$

Expansión en serie de Fourier de una función en un intervalo finito. Fourier.

Introducción

Expansiones de medio corrido

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Expansión en serie de Fourier de una función en un intervalo finito. Fourier.

Introducción

Expansiones de medio corrido

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta