La función impulso δ. Fourier.

La función impulso unitaria $\delta (t)$ , conocida también como función delta, se puede definir de varias maneras. Generalmente, se expresa mediante la siguiente relación

$\displaystyle \delta (t) = \left\{ \begin{matrix} 0 \quad t \ne 0 \\ \infty \quad t = 0 \end{matrix} \right.$

Esto indica que $\delta(t)$ es cero excepto en $t=0$ , donde se hace infinita, de tal manera que se cumpla con la segunda ecuación. Desarrollando la integral impropia con valores aproximados en sus límites de integración, se tiene lo siguiente,

$\displaystyle \int_{- \infty}^{\infty}{\delta(t) \, dt} = \int_{-\infty}^{-\varepsilon}{\delta(t) \, dt} + \int_{-\varepsilon}^{\varepsilon}{\delta(t) \, dt} + \int_{\varepsilon}^{\infty}{\delta(t) \, dt}$

por la definición de la función delta, resulta que

$\displaystyle \int_{- \infty}^{\infty}{\delta(t) \, dt} = \int_{-\infty}^{-\varepsilon}{0 \, dt} + \int_{-\varepsilon}^{\varepsilon}{\delta(t) \, dt} + \int_{\varepsilon}^{\infty}{0 \, dt}$

$\displaystyle \int_{- \infty}^{\infty}{\delta(t) \, dt} = \int_{-\varepsilon}^{\varepsilon}{\delta(t) \, dt}$

$\displaystyle \int_{- \infty}^{\infty}{\delta(t) \, dt} = 1$

donde $\varepsilon > 0$ .

La función delta también se puede definir en términos de las propiedades de sus integrales solamente, ésta es la definición que se utilizará. A partir de aquí, $\delta(t)$ se definirá en el sentido de la llamada función generalizada (o simbólica).

Suponiendo que la función de prueba $\phi(t)$ (llamada función de prueba) es una función continua, que se anula fuera de algún intervalo finito, entonces la función $\delta(t)$ se define como una función simbólica por la relación

$\displaystyle \int_{-\infty}^{\infty}{\delta(t) \phi(t) \, dt} = \phi(0)$

Esta expresión no tiene significado común de una integral definida, sino que la integral, así como la función $\delta(t)$ , están definidas por el número $\phi(0)$ asignado a la función $\phi(t)$ .

Con la interpretación anterior, resulta que $\delta(t)$ se puede tratar como si fuera una función ordinaria, excepto que nunca se hablará del valor de $\delta(t)$ , pero sí de los valores de las integrales en que aparece $\delta(t)$ .

Teoremas que se relacionan con la función δ

Teorema 1.

$\displaystyle \int_{-\infty}^{\infty}{\delta(t-t_0) \phi(t) \, dt} =\int_{-\infty}^{\infty}{\delta(t) \phi(t-t_0) \, dt} = \phi(t_0)$

$\displaystyle \int_{-\infty}^{\infty}{\delta(at) \phi(t) \, dt} = \frac{1}{|a|} \int_{-\infty}^{\infty}{\delta(t) \phi(\frac{1}{a}) \, dt} = \frac{1}{|a|} \phi(0)$

Teorema 2. Si $g(t)$ es una función continua en $t=t_0$ y $a<b$ , entonces

$\displaystyle \int_{a}^{b}{\delta(t-t_0) g(t) \, dt} = \left\{ \begin{matrix} g(t_0) \quad a<t_0<b \\0 \quad \quad b < t_0 < a \end{matrix} \right.$

Teorema 3. Si $a<b$

$\displaystyle \int_{a}^{b}{\delta(t-t_0) \, dt} = \left\{ \begin{matrix}1 \quad a < t_0 < b \\0 \quad b < t_0 < a \end{matrix} \right.$

Teorema 4. Si $f(t)$ es una función continua y $\phi(t)$ es una función de prueba arbitraria, entonces

$f(t) \delta(t) = f(0) \delta(t)$

$t \delta(t) = 0$

$\displaystyle \delta(at) = \frac{1}{|a|} \delta(t)$

$\displaystyle \delta(-t) = \delta(t)$

Derivadas de la función δ

La derivada $\delta'(t)$ de $\delta(t)$ está definida por la relación integral

$\displaystyle \int_{-\infty}^{\infty}{\delta' (t) \phi(t) \, dt} = -\int_{-\infty}^{\infty}{\delta(t) \phi'(t) \, dt} = \phi'(0)$

donde

$\displaystyle \delta'(t) = \frac{d}{dt}[\delta (t)]$ , $\displaystyle \phi'(0) = \left. \frac{d\phi}{dt} \right|_{t=0}$

La ecuación que muestra la definición de la derivada de delta, muestra que $\delta'(t) = \frac{d}{dt} [\delta (t)]$ es una función generalizada que asigna el valor $-\phi'(0)$ a la función de prueba.

La derivada enésima de la función $\delta$ es

$\displaystyle \delta^{(n)} (t) = \frac{d^n}{dt^n} [\delta(t)]$

Y también se puede definir lo siguiente

$\displaystyle \int_{-\infty}^{\infty}{\delta^{(n)} (t) \phi(t) \, dt} = (-1)^n \phi^{(n)}(0)$ ,

donde

$\displaystyle \phi^{(n)} (0) = \left. \frac{d^{n}}{dt^n} [\phi(t)] \right|_{t=0}$

Teoremas que relacionan las derivadas de la función δ

Teorema 5. Si $\phi(t)$ es una función de prueba tal que se anula fuera de algún intervalo, entonces

$\displaystyle \int_{-\infty}^{\infty}{f'(t) \delta(t) \, dt} = - \int_{-\infty}^{\infty}{f(t) \delta'(t) \, dt}$

que es consecuente con la definición ordinaria de una derivada de $f(t)$ si $f(t)$ es una función ordinaria cuya primera derivada es continua.

Teorema 6. Si $f(t)$ es una función continua y diferenciable, la regla del producto es

$\displaystyle [f(t) \delta(t)]' = f(t) \delta'(t) + f'(t) \delta(t)$

Teorema 7.

$f(t) \delta'(t) = f(0) \delta'(t) - f'(0) \delta(t)$

Teorema 8. La función δ es la derivada de la función $u(t)$ , la cual está definida por la relación

$\displaystyle \int_{-\infty}^{\infty}{u(t) \delta(t) \, dt} = \int_{-\infty}^{\infty}{\phi(t) \, dt}$

Teorema 9. La derivada de una función unitaria es

$\displaystyle u'(t) = \frac{d}{dt} [u(t)] = \delta (t)$

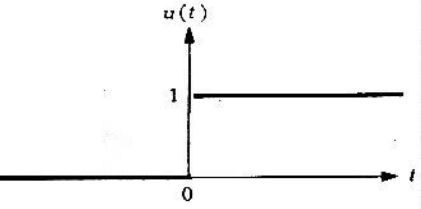
Función unitaria de Heaviside

La función generalizada (o función simbólica) $u(t)$ definida por el teorema 4

$\displaystyle \int_{-\infty}^{\infty}{u(t) \delta(t) \, dt} = \int_{-\infty}^{\infty}{\phi(t) \, dt}$ ,

se conoce como la función unitaria de Heaviside o función escalonada unitaria. Esto se puede definir como

$\displaystyle u(t) = \left\{ \begin{matrix} 1 \quad t>0 \\ 0 \quad t<0 \end{matrix} \right.$

La función no está definida para $t=0$ .

Se debe notar que la derivada de la función $u(t)$ es cero cuando $t<0$ y $t>0$ .

*Figura 1. Representación gráfica de la función unitaria de Heaviside.*

La derivada generalizada de «f(t)»

Si $f(t)$ es una función continua por tramos con discontinuidades súbitas $a_1$ , $a_2$ , $\cdots$ , en $t_1$ , $t_2$ , $\cdots$ , y la función $f'(t)$ está definida en todas partes excepto en estas discontinuidades de número finito, la derivada generalizada de $f(t)$ es