Series de Fourier de las derivadas de funciones periódicas discontinuas. Fourier

Se dice que la sucesión de una función generalizada $f_n(t)$ , donde $n=1, 2, \cdots$ , converge a la función generalizada $f(t)$ si y sólo si

$\displaystyle \lim_{n \rightarrow \infty}{\int_{-\infty}^{\infty}{f_n (t) \phi(t) \,dt}} = \int_{-\infty}^{\infty}{f(t) \phi (t) \, dt}$

para toda función de prueba $\phi(t)$ .

Análogamente, una serie

$\displaystyle \sum_{n=1}^{k}{f_n(t)}$

con funciones generalizadas que converge a la función generalizada $f(t)$ se puede diferenciar término por término. En otros términos,

$\displaystyle f'(t) = \sum_{n=1}^{k}{f'_n(t)}$

En este caso se dice que la serie converge en el sentido de funciones generalizadas, aunque en el sentido ordinario, la derivada de una serie convergente de funciones diferenciables puede, en general, no converger.

Al recordar que si $f(t)$ es periódica y continua, esta dada por

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_n t})}$

entonces $f'(t)$ también es periódica y se puede obtener diferenciando término por término, es decir

$\displaystyle f'(t) = \sum_{n=1}^{\infty}{(-n \omega_0 a_n \sin{n \omega_0 t} + n \omega_0 b_n \cos{n \omega_n t})}$

Problemas resueltos

Problema 1. Encontrar la serie de Fourier para la derivada de la forma de onda de la figura 1.

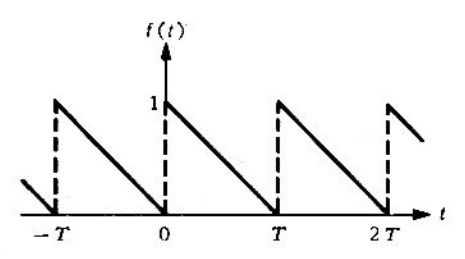
figura 2.5.1 — *Figura 1. Representación gráfica de la forma de onda del problema 1.*

Solución. La figura presenta una simetría escondida, para ello, se desplazará $1/2$ de la función para tener la siguiente forma

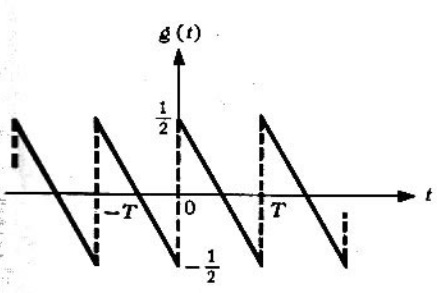
forma de onda del problema 3b — *Figura 2. Desplazamiento de la amplitud de la función «f(t)».*

Y la nueva función a tomar para resolver este problema es $\displaystyle g(t) = f(t) - \frac{1}{2}$ , donde $g(t)$ es una función impar. De $f(t)$ (de la figura 2.5.1), la función es ( $0 < t < T$ )

$\displaystyle f(t) - f(t_1) = \left[ \frac{f(t_2) - f(t_1)}{t_2 - t_1} \right] (t - t_1)$

$\displaystyle f(t) - 1 = \left( \frac{-\frac{1}{2} - \frac{1}{2}}{T - 0} \right) (t - 0)$

$\displaystyle f(t) - 1 = \left(- \frac{1}{T} \right) (t)$

$\displaystyle f(t) - 1 = - \frac{1}{T} t$

$\displaystyle f(t) = 1 - \frac{1}{T} t$

Por lo que $g(t)$ (de la figura 2) es

$\displaystyle g(t) = f(t) - \frac{1}{2}$

$\displaystyle g(t) = 1 - \frac{1}{T} t - \frac{1}{2}$

$\displaystyle g(t) = \frac{1}{2} - \frac{1}{T} t$

Si $g(t)$ es impar, la serie de Fourier es

$\displaystyle g(t) = \sum_{n=1}^{\infty}{b_n \sin{n \omega_0 t}}$

Calculando $b_n$

$\displaystyle b_n = \frac{4}{T} \int_{0}^{T/2}{g(t) \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{4}{T} \int_{0}^{T/2}{\left(\frac{1}{2} - \frac{1}{T} t \right) \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{4}{T} \int_{0}^{T/2}{\frac{1}{2} \sin{n \omega_0 t} \, dt} + \frac{4}{T} \int_{0}^{T/2}{\left(- \frac{1}{T} t \right) \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{2}{T} \int_{0}^{T/2}{\sin{n \omega_0 t} \, dt} - \frac{4}{T^2} \int_{0}^{T/2}{t \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{1}{n \omega_0} \right) \cos{n \omega_0 t} + C \right]_{0}^{T/2} - \frac{4}{T^2} \left[\left(-\frac{1}{n \omega_0} \right) t \cos{n \omega_0 t} + \left( \frac{1}{n \omega_0} \right)^2 \sin{n \omega_0 t} + C \right]_{0}^{T/2}$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{1}{n \omega_0} \right) \cos{n \omega_0 (\frac{T}{2})} + \left(\frac{1}{n \omega_0} \right) \cos{n \omega_0 (0)} \right] - \frac{4}{T^2} \left[\left(-\frac{1}{n \omega_0} \right) (\frac{T}{2}) \cos{n \omega_0 (\frac{T}{2})} + \left( \frac{1}{n \omega_0} \right)^2 \sin{n \omega_0 (\frac{T}{2})} - \left(-\frac{1}{n \omega_0} \right) (0) \cos{n \omega_0 (0)} - \left( \frac{1}{n \omega_0} \right)^2 \sin{n \omega_0 (0)} \right]$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{1}{n \omega_0} \right) \cos{n \omega_0 (\frac{T}{2})} + \left(\frac{1}{n \omega_0} \right) (1) \right] - \frac{4}{T^2} \left[\left(-\frac{1}{n \omega_0} \right) (\frac{T}{2}) \cos{n \omega_0 (\frac{T}{2})} + \left( \frac{1}{n \omega_0} \right)^2 \sin{n \omega_0 (\frac{T}{2})} - (0) (1) - \left( \frac{1}{n \omega_0} \right)^2 (0) \right]$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{1}{n \omega_0} \right) \cos{n \omega_0 (\frac{T}{2})} + \left(\frac{1}{n \omega_0} \right) \right] - \frac{4}{T^2} \left[\left(-\frac{1}{n \omega_0} \right) (\frac{T}{2}) \cos{n \omega_0 (\frac{T}{2})} + \left( \frac{1}{n \omega_0} \right)^2 \sin{n \omega_0 (\frac{T}{2})} \right]$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{1}{n \left(\frac{2\pi}{T} \right)} \right) \cos{n \left(\frac{2\pi}{T} \right) (\frac{T}{2})} + \left(\frac{1}{n \left(\frac{2\pi}{T} \right)} \right) \right] - \frac{4}{T^2} \left[\left(-\frac{1}{n \left(\frac{2\pi}{T} \right)} \right) (\frac{T}{2}) \cos{n \left(\frac{2\pi}{T} \right) (\frac{T}{2})} + \left( \frac{1}{n \left(\frac{2\pi}{T} \right)} \right)^2 \sin{n \left(\frac{2\pi}{T} \right) (\frac{T}{2})} \right]$

$\displaystyle b_n = \frac{2}{T} \left[- \left(\frac{T}{2 n \pi} \right) \cos{n \pi} + \left(\frac{T}{2n \pi} \right) \right] - \frac{4}{T^2} \left[ \left(- \frac{T^2}{4 n \pi} \right) \cos{n \pi} + \left( \frac{T}{2 n \pi} \right)^2 \sin{n \pi} \right]$

$\displaystyle b_n = \frac{2}{T} \left(- \frac{T}{2 n \pi} \cos{n \pi} + \frac{T}{2n \pi} \right) - \frac{4}{T^2} \left( - \frac{T^2}{4 n \pi} \cos{n \pi} + \frac{T^2}{4 n^2 \pi^2} \sin{n \pi} \right)$

$\displaystyle b_n = - \frac{1}{n \pi} \cos{n \pi} + \frac{1}{n \pi} + \frac{1}{n \pi} \cos{n \pi} - \frac{1}{n^2 \pi^2} \sin{n \pi}$

$\displaystyle b_n = \frac{1}{n \pi} - \frac{1}{n^2 \pi^2} \sin{n \pi}$

Si $n=1,3,5, \cdots$

$\displaystyle b_n = \frac{1}{n \pi} - \frac{1}{n^2 \pi^2} \sin{n \pi}$

$\displaystyle b_n = \frac{1}{n \pi} - \frac{1}{n^2 \pi^2} (0)$

$\displaystyle b_n = \frac{1}{n \pi}$

Si $n=2,4,6, \cdots$

$\displaystyle b_n = \frac{1}{n \pi} - \frac{1}{n^2 \pi^2} \sin{n \pi}$

$\displaystyle b_n = \frac{1}{n \pi} - \frac{1}{n^2 \pi^2} (0)$

$\displaystyle b_n = \frac{1}{n \pi}$

Entonces, $b_n$ es

$\displaystyle b_n = \frac{1}{n \pi}$

Regresando a la serie de Fourier para $g(t)$

$\displaystyle g(t) = \sum_{n=1}^{\infty}{b_n \sin{n \omega_0 t}}$

$\displaystyle g(t) = \sum_{n=1}^{\infty}{\left(\frac{1}{n \pi} \right) \sin{n \omega_0 t}}$

Regresando a $f(t)$ , se obtiene el resultado final

$\displaystyle g(t) = f(t) - \frac{1}{2}$

$\displaystyle f(t) = \frac{1}{2} + g(t)$

$\displaystyle f(t) = \frac{1}{2} + \sum_{n=1}^{\infty}{\left(\frac{1}{n \pi} \right) \sin{n \omega_0 t}}$

$\displaystyle \therefore f(t) = \frac{1}{2} + \frac{1}{\pi} \sum_{n=1}^{\infty}{\frac{1}{n} \sin{n \omega_0 t}}$

De este resultado, se diferencia término por término

$\displaystyle f(t) = \frac{1}{2} + \frac{1}{\pi} \sum_{n=1}^{\infty}{\frac{1}{n} \sin{n \omega_0 t}}$

$\displaystyle \frac{d}{dt} [f(t)] = \frac{d}{dt} \left[\frac{1}{2} + \frac{1}{\pi} \sum_{n=1}^{\infty}{\frac{1}{n} \sin{n \omega_0 t}} \right]$

$\displaystyle f'(t) = \frac{1}{\pi} \sum_{n=1}^{\infty}{\frac{1}{n} n \omega_0 \cos{n \omega_0 t}}$

$\displaystyle f'(t) = \frac{\omega_0 }{\pi} \sum_{n=1}^{\infty}{\cos{n \omega_0 t}}$

$\displaystyle f'(t) = \frac{\frac{2\pi}{T}}{\pi} \sum_{n=1}^{\infty}{\cos{n \frac{2\pi}{T} t}}$

$\displaystyle \therefore f'(t) = \frac{2}{T} \sum_{n=1}^{\infty}{\cos{\frac{2n \pi}{T} t}}$

Recordando que

$\displaystyle f'(t) = - \frac{1}{T} + \sum_{n=-\infty}^{\infty}{\delta (t-nT)}$

Se observa que el resultado de la serie de Fourier del problema P1 no es una serie convergente en el sentido ordinario, pero se puede decir que esa serie converge a la función generalizada en el sentido de una función generalizada.

Si se igualan ambas ecuaciones, se obtiene un resultado, la cual, es la expresión en de serie de Fourier de un tren periódico de impulsos unitarios, es decir

$\displaystyle f'(t) = \frac{2}{T} \sum_{n=1}^{\infty}{\cos{\frac{2n \pi}{T} t}}$

$\displaystyle - \frac{1}{T} + \sum_{n=-\infty}^{\infty}{\delta (t-nT)} = \frac{2}{T} \sum_{n=1}^{\infty}{\cos{\frac{2n \pi}{T} t}}$

$\displaystyle \sum_{n=-\infty}^{\infty}{\delta (t-nT)} = \frac{1}{T} + \frac{2}{T} \sum_{n=1}^{\infty}{\cos{\frac{2n \pi}{T} t}}$

$\displaystyle \sum_{n=-\infty}^{\infty}{\delta (t-nT)} = \frac{1}{T} + \frac{2}{T} \sum_{n=1}^{\infty}{\cos{n \omega_0 t}}$

Esta ecuación muestra que el tren periódico de impulsos unitarios consiste de un término constante $1/T$ y una suma de armónicos todos con la misma amplitud de $2/T$ .

El tren periódico de impulsos unitarios es una función muy útil y por consiguiente es conveniente denotar esta función mediante un símbolo especial $\delta_T (t)$ . De este modo

$\displaystyle \delta_T (t) = \sum_{n=-\infty}^{\infty}{\delta (t-nT)}$

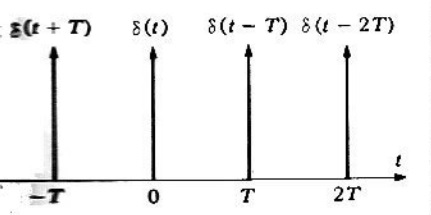
figura 2.5.3 — *Figura 3. Representación gráfica de un tren periódico de impulsos unitarios.*

¿Cómo deducir la serie de Fourier para un tren periódico de impulsos unitarios δ_T?

Suponiendo que

$\displaystyle \delta_T (t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_0 t})}$

donde se ha reemplazado $f(t)$ por $\delta_T (t)$ . En el caso de $a_0$

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{T/2}{\delta_T (t) \, dt}$

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{T/2}{\delta (t) \, dt}$

$\displaystyle a_0 = \frac{2}{T} (1) = \frac{2}{T}$

En el caso de $a_n$

$\displaystyle a_n = \frac{2}{T} \int_{-T/2}^{T/2}{\delta_T (t) \cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \frac{2}{T} \int_{-T/2}^{T/2}{\delta (t) \cos{n \omega_0 t} \, dt}$

$\displaystyle a_n = \left. \frac{2}{T} \cos{n \omega_0 t} \right|_{t=0}$

$\displaystyle a_n = \frac{2}{T} \cos{0} = \frac{2}{T}$

Y en el caso de $b_n$

$\displaystyle b_n = \frac{2}{T} \int_{-T/2}^{T/2}{\delta_T (t) \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{2}{T} \int_{-T/2}^{T/2}{\delta (t) \sin{n \omega_0 t} \, dt}$

$\displaystyle b_n = \frac{2}{T} \left. \sin{n \omega_0 t} \right|_{t=0}$

$\displaystyle b_n = \frac{2}{T} \sin{0} = 0$

Regresando

$\displaystyle \delta_T (t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_0 t})}$

$\displaystyle \delta_T (t) = \frac{1}{2} \cdot \frac{2}{T} + \sum_{n=1}^{\infty}{(\frac{2}{T} \cos{n \omega_0 t} + (0) \sin{n \omega_0 t})}$

$\displaystyle \delta_T (t) = \frac{1}{T} + \sum_{n=1}^{\infty}{\frac{2}{T} \cos{n \omega_0 t}}$

$\displaystyle \delta_T (t) = \frac{1}{T} + \frac{2}{T} \sum_{n=1}^{\infty}{\cos{n \omega_0 t}}$

$\displaystyle \therefore \sum_{n=1}^{\infty}{\delta (t - nT)} = \frac{1}{T} + \frac{2}{T} \sum_{n=1}^{\infty}{\cos{n \omega_0 t}}$

donde $\displaystyle \omega_0 = \frac{2\pi}{T}$ .

Series de Fourier de las derivadas de funciones periódicas discontinuas. Fourier

Problemas resueltos

¿Cómo deducir la serie de Fourier para un tren periódico de impulsos unitarios δ_T?

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Series de Fourier de las derivadas de funciones periódicas discontinuas. Fourier

Problemas resueltos

¿Cómo deducir la serie de Fourier para un tren periódico de impulsos unitarios δT?

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

¿Cómo deducir la serie de Fourier para un tren periódico de impulsos unitarios δ_T?