Forma compleja de las series de Fourier. Fourier.

Introducción

Considerando la serie de Fourier de una función periódica $f(t)$ , como

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_0 t})}$

donde $\omega_0 = 2\pi/T$ , el seno y coseno se puede expresar en términos de los exponenciales como

$\displaystyle \sin{n \omega_0 t} = \frac{e^{j n \omega_0 t} - e^{-j n \omega_0 t}}{2j}$

$\displaystyle \cos{n \omega_0 t} = \frac{e^{j n \omega_0 t} + e^{-j n \omega_0 t}}{2}$

Sustituyendo esto en la serie de Fourier

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{\left[a_n \cdot \left(\frac{e^{j n \omega_0 t} + e^{-j n \omega_0 t}}{2} \right) + b_n \cdot \left(\frac{e^{j n \omega_0 t} - e^{-j n \omega_0 t}}{2j} \right) \right]}$

$\displaystyle f(t) = \frac{1}{2} a_0 + \frac{1}{2} \sum_{n=1}^{\infty}{\left[a_n \cdot \left(e^{j n \omega_0 t} + e^{-j n \omega_0 t} \right) - jb_n \cdot \left(e^{j n \omega_0 t} - e^{-j n \omega_0 t} \right) \right]}$

$\displaystyle f(t) = \frac{1}{2} a_0 + \frac{1}{2} \sum_{n=1}^{\infty}{\left(a_n e^{j n \omega_0 t} + a_n e^{-j n \omega_0 t} - jb_n e^{j n \omega_0 t} + j b_n e^{-j n \omega_0 t} \right)}$

$\displaystyle f(t) = \frac{1}{2} a_0 + \frac{1}{2} \sum_{n=1}^{\infty}{\left[(a_n - j b_n) e^{j n \omega_0 t} + (a_n + j b_n) e^{-j n \omega_0 t} \right]}$

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{\left[\frac{1}{2} (a_n - j b_n) e^{j n \omega_0 t} + \frac{1}{2} (a_n + j b_n) e^{-j n \omega_0 t} \right]}$

$\displaystyle f(t) = c_0 + \sum_{n=1}^{\infty}{ \left(c_n e^{j n \omega_0 t} +c_{-n} e^{-j n \omega_0 t} \right)}$

$\displaystyle f(t) = c_0 + \sum_{n=1}^{\infty}{c_n e^{j n \omega_0 t}} + \sum_{n=1}^{\infty}{c_{-n} e^{-j n \omega_0 t}}$

$\displaystyle f(t) = c_0 + \sum_{n=1}^{\infty}{c_n e^{j n \omega_0 t}} + \sum_{n=-1}^{-\infty}{c_{n} e^{j n \omega_0 t}}$

$\displaystyle f(t) = \sum_{n=1}^{\infty}{c_n e^{j n \omega_0 t}} + c_0 + \sum_{n=-1}^{-\infty}{c_{n} e^{j n \omega_0 t}}$

$\displaystyle f(t) = \sum_{n=-\infty}^{\infty}{c_n e^{j n \omega_0 t}}$

Esta última expresión se denomina forma compleja de la serie de Fourier de $f(t)$ , o serie compleja de Fourier de $f(t)$ .

El coeficiente $c_0$ es

$\displaystyle c_0 = \frac{1}{2} a_0$

$\displaystyle c_0 = \frac{1}{2} \cdot \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \, dt}$

$\displaystyle c_0 = \frac{1}{T} \int_{-T/2}^{T/2}{f(t) \, dt}$

El coeficiente $c_n$ es

$\displaystyle c_n = \frac{1}{2} (a_n - j b_n)$

$\displaystyle c_n = \frac{1}{2} \left[\frac{2}{T} \int_{-T/2}^{T/2}{f(t) \cos{n\omega_0 t} \, dt} - j\frac{2}{T} \int_{-T/2}^{T/2}{f(t) \sin{n\omega_0 t} \, dt}\right]$

$\displaystyle c_n = \frac{1}{T} \int_{-T/2}^{T/2}{f(t) \cos{n\omega_0 t} \, dt} - j\frac{1}{T} \int_{-T/2}^{T/2}{f(t) \sin{n\omega_0 t} \, dt}$

$\displaystyle c_n = \frac{1}{T} \int_{-T/2}^{T/2}{f(t) (\cos{n\omega_0 t} - j \sin{n\omega_0 t}) \, dt}$

$\displaystyle c_n = \frac{1}{T} \int_{-T/2}^{T/2}{f(t) e^{-jn\omega_0 t} \, dt}$

Y el coeficiente $c_{-n}$ es

$\displaystyle c_{-n} = \frac{1}{2} (a_n + j b_n)$

$\displaystyle c_{-n} = \frac{1}{2} \left[\frac{2}{T} \int_{-T/2}^{T/2}{f(t) \cos{n\omega_0 t} \, dt} + j\frac{2}{T} \int_{-T/2}^{T/2}{f(t) \sin{n\omega_0 t} \, dt}\right]$

$\displaystyle c_{-n} = \frac{1}{T} \int_{-T/2}^{T/2}{f(t) \cos{n\omega_0 t} \, dt} + j\frac{1}{T} \int_{-T/2}^{T/2}{f(t) \sin{n\omega_0 t} \, dt}$

$\displaystyle c_{-n} = \frac{1}{T} \int_{-T/2}^{T/2}{f(t) (\cos{n\omega_0 t} + j \sin{n\omega_0 t}) \, dt}$

$\displaystyle c_{-n} = \frac{1}{T} \int_{-T/2}^{T/2}{f(t) e^{jn\omega_0 t} \, dt}$

Si $f(t)$ es real, entonces

$c_{-n} = c^*_n$

lo cual indica el complejo conjugado.

Puesto que $f(t) e^{-j n \omega_0 t}$ es periódica con período T, se tiene que $c_n$ también se puede hallar a partir de la fórmula

$\displaystyle c_n = \frac{1}{T} \int_{0}^{T}{f(t) e^{- j n\omega_0 t} \, dt}$

Ahora, si

$\displaystyle c_n = |c_n| e^{j \phi n}$

$\displaystyle c_{-n} = c_{n}^* = |c_n| e^{-j \phi_n}$

Entonces

$\displaystyle c_n = \frac{1}{2} \sqrt{a_n^2 + b_n^2}$

$\displaystyle \phi_n = \tan^{-1}{\left(-\frac{b_n}{a_n}\right)}$

para todos los valores de $n$ , excepto $n=0$ . En este caso $c_0$ es real y

$\displaystyle c_0 = \frac{1}{2} a_0$

Problemas resueltos

Problema 1. Encontrar la serie compleja de Fourier, para la función diente de sierra que se muestra en la figura 1, definida por

$\displaystyle f(t) = \frac{A}{T} t$

en $0 < t T$ y $f(t + T) = f(t)$ .

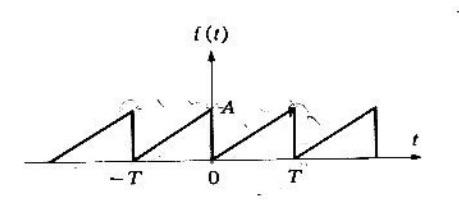
Figura 3.1.1 Función diente de sierra — *Figura 1. Función diente de sierra.*

Solución. La representación de $f(t)$ en serie compleja de Fourier está dada por

$\displaystyle f(t) = \sum_{n=-\infty}^{\infty}{c_n e^{jn\omega_0 t}}$

donde $\omega_0 = 2\pi/T$ . El valor de $c_n$ es

$\displaystyle c_n = \frac{1}{T} \int_{0}^{T}{f(t) e^{-jn\omega_0 t} \, dt}$

$\displaystyle c_n = \frac{1}{T} \int_{0}^{T}{\frac{A}{T} t e^{-jn\omega_0 t} \, dt}$

$\displaystyle c_n = \frac{1}{T} \cdot \frac{A}{T} \int_{0}^{T}{t e^{-jn\omega_0 t} \, dt} = \frac{A}{T^2} \int_{0}^{T}{t e^{-jn\omega_0 t} \, dt}$

$\displaystyle c_n = \frac{A}{T^2} \left[- \frac{1}{j n \omega_0} t e^{-j n \omega_0 t} - \left( \frac{1}{j n \omega_0} \right)^2 e^{-j n \omega_0 t} \right]_{0}^{T}$

$\displaystyle c_n = \frac{A}{T^2} \left[j \frac{1}{n \omega_0} t e^{-j n \omega_0 t} - \left( \frac{1}{j n \omega_0} \right)^2 e^{-j n \omega_0 t} \right]_{0}^{T}$

$\displaystyle c_n = \frac{A}{T^2} \left[j \frac{1}{n \omega_0} (T) e^{-j n \omega_0 T} - \left( \frac{1}{j n \omega_0} \right)^2 e^{-j n \omega_0 T} \right] - \frac{A}{T^2} \left[j \frac{1}{n \omega_0} (0) e^{-j n \omega_0 (0)} - \left( \frac{1}{j n \omega_0} \right)^2 e^{-j n \omega_0 (0)} \right]$

$\displaystyle c_n = \frac{A}{T^2} \left[j \frac{T}{n \omega_0} e^{-j n \omega_0 T} - \left( \frac{1}{j n \omega_0} \right)^2 e^{-j n \omega_0 T} \right] + \frac{A}{T^2} \cdot \left( \frac{1}{j n \omega_0} \right)^2$

$\displaystyle c_n = \frac{A}{T^2} \left[j \frac{T}{n \frac{2\pi}{T}} e^{-j n \frac{2\pi}{T} T} - \left( \frac{1}{j n \frac{2\pi}{T}} \right)^2 e^{-j n \frac{2\pi}{T} T} \right] + \frac{A}{T^2} \cdot \left( \frac{1}{j n \frac{2\pi}{T}} \right)^2$

$\displaystyle c_n = \frac{A}{T^2} \left[j \frac{T^2}{2 n \pi} e^{-j 2 n \pi} - \left( \frac{T}{j 2 n \pi} \right)^2 e^{-j 2 n \pi} \right] + \frac{A}{T^2} \cdot \left( \frac{T}{j 2 n \pi} \right)^2$

$\displaystyle c_n = \frac{A}{T^2} \left(j \frac{T^2}{2 n \pi} e^{-j 2 n \pi} - \frac{T^2}{4 n^2 \pi^2} e^{-j 2 n \pi} \right) + \frac{A}{T^2} \cdot \left( \frac{T^2}{4 n^2 \pi^2} \right)$

$\displaystyle c_n = j \frac{A}{2 n \pi} e^{-j 2 n \pi} - \frac{A}{4 n^2 \pi^2} e^{-j 2 n \pi} + \frac{A}{4 n^2 \pi^2}$

$\displaystyle c_n = j \frac{A}{2 n \pi} (1) - \frac{A}{4 n^2 \pi^2} (1) + \frac{A}{4 n^2 \pi^2} = j \frac{A}{2 n \pi}$

$\displaystyle c_n = \frac{A}{2n \pi}e^{j \frac{\pi}{2}}$

De este último resultado, si $n=0$ , no estará definido y no tendría significado. Para ello, cuando $n=0$ , el valor de $c_0$ es

$\displaystyle c_0 = \frac{1}{2} a_0$

$\displaystyle c_0 = \frac{1}{2}\cdot \frac{2}{T} \int_{0}^{T}{f(t) \, dt}$

$\displaystyle c_0 = \frac{1}{T} \int_{0}^{T}{\frac{A}{T} t \, dt}$

$\displaystyle c_0 = \frac{A}{T^2} \int_{0}^{T}{t \, dt}$

$\displaystyle c_0 = \frac{A}{T^2} \left[\frac{1}{2} t^2 + C \right]_{0}^{T}$

$\displaystyle c_0 = \frac{A}{T^2} \left(\frac{1}{2} T^2 - \frac{1}{2} (0) \right)$

$\displaystyle c_0 = \frac{A}{T^2} \cdot \frac{1}{2} T^2$

$\displaystyle c_0 = \frac{A}{2}$

Regresando a la serie compleja de Forier, se tiene el resultado final

$\displaystyle f(t) = \sum_{n=-\infty}^{\infty}{c_n e^{jn\omega_0 t}}$

$\displaystyle f(t) = \sum_{n=-1}^{\infty}{c_n e^{jn\omega_0 t}} + c_0 + \sum_{n=1}^{\infty}{c_n e^{jn\omega_0 t}}$

$\displaystyle f(t) = c_0 + \sum_{n=-\infty}^{-1}{c_n e^{jn\omega_0 t}} + \sum_{n=1}^{\infty}{c_n e^{jn\omega_0 t}}$

$\displaystyle f(t) = \frac{A}{2} + \sum_{n=-\infty}^{-1}{\frac{A}{2n \pi}e^{j \frac{\pi}{2}} e^{jn\omega_0 t}} + \sum_{n=1}^{\infty}{\frac{A}{2n \pi}e^{j \frac{\pi}{2}} e^{jn\omega_0 t}}$

$\displaystyle \therefore f(t) = \frac{A}{2} + \frac{A}{2\pi} \sum_{n=-\infty}^{-1}{\frac{1}{n}e^{j (\frac{\pi}{2} + n\omega_0 t)}} + \frac{A}{2\pi} \sum_{n=1}^{\infty}{\frac{1}{n}e^{j( \frac{\pi}{2} + n\omega_0 t)}}$

Problema 2. Reducir el resultado del problema 1 a la forma trigonométrica de la serie de Forier.

Solución. Del valor de $a_0$

$\displaystyle c_0 = \frac{1}{2} a_0$

$\displaystyle 2 c_0 = a_0$

$a_0 = 2 c_0$

$a_0 = 2 \cdot \frac{A}{2}$

$a_0 = A$

El valor de $a_n$ es

$\displaystyle c_n = \frac{1}{2} (a_n - j b_n)$

$\displaystyle 2c_n = a_n - j b_n$

$\displaystyle 2c_n - a_n = - jb_n$

$\displaystyle - 2c_n + a_n = jb_n$

$\displaystyle c_{-n} = c_n^* = \frac{1}{2} (a_n + j b_n)$

$\displaystyle 2c_{-n} = a_n + j b_n$

$\displaystyle 2c_{-n} - a_n = j b_n$

$\displaystyle - 2c_n + a_n = 2c_{-n} - a_n$

$\displaystyle 2a_n = 2c_{-n} + 2 c_{n}$

$\displaystyle a_n = c_{-n} + c_{n}$

$\displaystyle a_n = 2 \Re[c_n]$

$\displaystyle a_n = 2 \Re \left[\frac{A}{2n \pi}e^{j \frac{\pi}{2}} \right] = 2 \Re \left[ j\frac{A}{2n \pi} \right]$

$a_n = 0$

donde $\Re$ significa «parte real de » (algunos autores lo denotan como $Re$ ).

El valor de $b_n$ es

$\displaystyle c_n = \frac{1}{2} (a_n - j b_n) \quad \quad \quad c_{-n} = c_n^* = \frac{1}{2} (a_n + j b_n)$

$\displaystyle 2c_n = a_n - j b_n \quad \quad \quad 2c_{-n} = a_n + j b_n$

$\displaystyle 2c_n + j b_n = a_n \quad \quad \quad 2c_{-n} - j b_n = a_n$

$\displaystyle 2c_n + j b_n = 2c_{-n} - j b_n$

$\displaystyle 2 j b_n = 2c_{-n} - 2c_n$

$\displaystyle b_n = \frac{1}{j} c_{-n} - \frac{1}{j} c_n$

$\displaystyle b_n = - j c_{-n} + jc_n$

$\displaystyle b_n = jc_n - j c_{-n}$

$\displaystyle b_n = j(c_n - c_{-n}) = - 2 \Im[c_n]$

$\displaystyle b_n = - 2 \Im \left[\frac{A}{2n \pi}e^{j \frac{\pi}{2}} \right] = - 2 \Im \left[j \frac{A}{2n \pi} \right]$

$\displaystyle b_n = 2 \cdot \frac{A}{2n \pi}$

$\displaystyle b_n = \frac{A}{n \pi}$

donde $\Im$ significa «parte imaginaria de » (algunos autores lo denotan como $Im$ ).

Entonces, la serie trigonométrica de Fourier esperada es

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_0 t})}$

$\displaystyle f(t) = \frac{1}{2} (A)+ \sum_{n=1}^{\infty}{\left[ (0) \cos{n \omega_0 t} + (-\frac{A}{n \pi}) \sin{n \omega_0 t} \right]}$

$\displaystyle \therefore f(t) = \frac{A}{2} - \frac{A}{\pi} \sum_{n=1}^{\infty}{\frac{1}{n} \sin{n \omega_0 t}}$

Problema 3. Encontrar la serie de Fourier en forma compleja de la función periódica sinusoide rectificada $f(t)$ que se muestra en la figura 2, definida por

$\displaystyle f(t) = A \sin{\pi t}$

en $0 < t < T$ y $f(t + T) = f(t)$ .

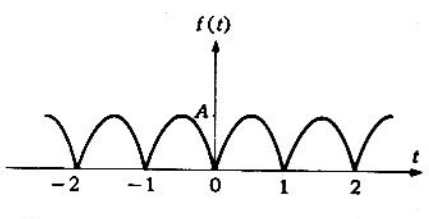
Figura 3.1.2 Función periódica sinusoide rectificada — *Figura 2. Función periódica sinusoide rectificada.*

Solución. La representación de $f(t)$ en serie compleja de Fourier está dada por

$\displaystyle f(t) = \sum_{n=-\infty}^{\infty}{c_n e^{jn\omega_0 t}}$

donde $\omega_0 = 2\pi/T$ . Como $T=1$ , $\omega_0 = 2\pi$ , y

$\displaystyle f(t) = \sum_{n=-\infty}^{\infty}{c_n e^{j 2n\pi t}}$

El valor de $c_n$ es

$\displaystyle c_n = \frac{1}{T} \int_{0}^{T}{f(t) e^{-jn\omega_0 t} \, dt}$

$\displaystyle c_n = \int_{0}^{1}{A \sin{\pi t} e^{-j 2 n \pi t} \, dt}$

$\displaystyle c_n = A \int_{0}^{1}{\sin{\pi t} e^{-j2 n \pi t} \, dt}$

$\displaystyle c_n = A \int_{0}^{1}{\frac{1}{j2} (e^{j \pi t} - e^{-j \pi t}) e^{-j 2 n\pi t} \, dt}$

$\displaystyle c_n = \frac{A}{j2} \int_{0}^{1}{(e^{j \pi t} - e^{-j \pi t}) e^{-j 2 n\pi t} \, dt}$

$\displaystyle c_n = \frac{A}{j2} \int_{0}^{1}{(e^{j \pi t - j 2 n \pi t} - e^{-j \pi t - j 2 n \pi t}) \, dt}$

$\displaystyle c_n = \frac{A}{j2} \int_{0}^{1}{e^{j \pi t - j 2 n \pi t} \, dt} - \frac{A}{j2} \int_{0}^{1}{(e^{-j \pi t - j 2 n \pi t} \, dt}$

$\displaystyle c_n = \frac{A}{j2} \int_{0}^{1}{e^{j \pi t(1 - 2 n)} \, dt} - \frac{A}{j2} \int_{0}^{1}{e^{-j \pi t(1 + 2 n)} \, dt}$

$\displaystyle c_n = \frac{A}{j2} \left[\frac{1}{j \pi(1-2n)} e^{j \pi t(1 - 2 n)} \right]_{0}^{1} - \frac{A}{j2} \left[-\frac{1}{j \pi (1+2n)} e^{-j \pi t(1 + 2 n)} \right]_{0}^{1}$

$\displaystyle c_n = \frac{A}{j2} \left[\frac{1}{j \pi(1-2n)} e^{j \pi (1)(1 - 2 n)} - \frac{1}{j \pi(1-2n)} e^{j \pi (0)(1 - 2 n)} \right] - \frac{A}{j2} \left[-\frac{1}{j \pi (1+2n)} e^{-j \pi (1) (1 + 2 n)} + \frac{1}{j \pi (1+2n)} e^{-j \pi (0)(1 + 2 n)} \right]$

$\displaystyle c_n = \frac{A}{j2} \left[\frac{1}{j \pi(1-2n)} e^{j \pi (1 - 2 n)} - \frac{1}{j \pi(1-2n)} (1) \right] - \frac{A}{j2} \left[-\frac{1}{j \pi (1+2n)} e^{-j \pi (1 + 2 n)} + \frac{1}{j \pi (1+2n)} (1) \right]$

$\displaystyle c_n = \frac{A}{j2} \left[\frac{1}{j \pi(1-2n)} e^{j \pi (1 - 2 n)} - \frac{1}{j \pi(1-2n)} \right] - \frac{A}{j2} \left[-\frac{1}{j \pi (1+2n)} e^{-j \pi (1 + 2 n)} + \frac{1}{j \pi (1+2n)} \right]$

$\displaystyle c_n = \frac{A}{j2} \cdot \frac{1}{j \pi(1-2n)} \left[e^{j \pi (1 - 2 n)} - 1 \right] - \frac{A}{j2} \cdot \frac{1}{j \pi (1+2n)} \left[-e^{-j \pi (1 + 2 n)} + 1 \right]$

$\displaystyle c_n = \frac{A}{j2} \cdot \frac{1}{j \pi(1-2n)} \left[e^{j \pi (1 - 2 n)} - 1 \right] + \frac{A}{j2} \cdot \frac{1}{j \pi (1+2n)} \left[e^{-j \pi (1 + 2 n)} - 1 \right]$

$\displaystyle c_n = - \frac{A}{2 \pi(1-2n)} \left[e^{j \pi (1 - 2 n)} - 1 \right] - \frac{A}{2\pi (1+2n)} \left[e^{-j \pi (1 + 2 n)} - 1 \right]$

$\displaystyle c_n = - \frac{A}{2 \pi(1-2n)} \left(e^{j \pi} e^{- j 2 n \pi} - 1 \right) - \frac{A}{2\pi (1+2n)} \left(e^{-j \pi} e^{-j 2 n\pi} - 1 \right)$

$\displaystyle c_n = - \frac{A}{2 \pi(1-2n)} \left(- 1 - 1 \right) - \frac{A}{2\pi (1+2n)} \left(- 1 - 1 \right)$

$\displaystyle c_n = - \frac{A}{2 \pi(1-2n)} \left(- 2 \right) - \frac{A}{2\pi (1+2n)} \left(- 2 \right)$

$\displaystyle c_n = \frac{A}{\pi(1-2n)} + \frac{A}{\pi (1+2n)}$

$\displaystyle c_n = \frac{A}{\pi} \left[ \frac{1 - 2n + 1 + 2n}{(1-2n)(1+2n)} \right]$

$\displaystyle c_n = \frac{A}{\pi} \left( \frac{2}{1 + 2n - 2n - 4n^2} \right)$

$\displaystyle c_n = \frac{A}{\pi} \left( \frac{2}{1 - 4n^2} \right)$

$\displaystyle c_n = \frac{2A}{\pi (1 - 4n^2)}$

El valor de $c_0$ es

$\displaystyle c_0 = \frac{1}{2} a_0$

$\displaystyle c_0 = \frac{1}{2}\cdot \frac{2}{T} \int_{0}^{T}{f(t) \, dt}$

$\displaystyle c_0 = \frac{1}{T} \int_{0}^{T}{f(t) \, dt}$

$\displaystyle c_0 = \frac{1}{1} \int_{0}^{1}{f(t) \, dt} = \int_{0}^{1}{f(t) \, dt}$

$\displaystyle c_0 = \int_{0}^{1}{A \sin{\pi t} \, dt}$

$\displaystyle c_0 = A \int_{0}^{1}{\sin{\pi t} \, dt}$

$\displaystyle c_0 = A \left[- \frac{1}{\pi} \cos{\pi t} +C \right]_{0}^{1}$

$\displaystyle c_0 = A \left[- \frac{1}{\pi} \cos{\pi (1)} + \frac{1}{\pi} \cos{\pi (0)} \right]$

$\displaystyle c_0 = A \left(- \frac{1}{\pi} \cos{\pi} + \frac{1}{\pi} \cos{0} \right)$

$\displaystyle c_0 = A \left[- \frac{1}{\pi} (-1) + \frac{1}{\pi} (1) \right]$

$\displaystyle c_0 = A \left(\frac{1}{\pi} + \frac{1}{\pi} \right)$

$\displaystyle c_0 = A \cdot \frac{2}{\pi}$

$\displaystyle c_0 = \frac{2A}{\pi}$

Entonces, como el resultado de los coeficientes determinados concuerdan, se tiene el resultado final. Regresando

$\displaystyle f(t) = \sum_{n=-\infty}^{\infty}{c_n e^{j 2n\pi t}}$

$\displaystyle f(t) = \sum_{n=-\infty}^{\infty}{\frac{2A}{\pi (1 - 4n^2)} e^{j 2n\pi t}}$

$\displaystyle \therefore f(t) = \frac{2A}{\pi} \sum_{n=-\infty}^{\infty}{\frac{1}{(1 - 4n^2)} e^{j 2n\pi t}}$

Problema 4. Reducir el resultado del problema 3 a la forma trigonométrica de la serie de Forier.

Solución. Del valor de $a_0$

$\displaystyle c_0 = \frac{1}{2} a_0$

$\displaystyle 2 c_0 = a_0$

$a_0 = 2 c_0$

$\displaystyle a_0 = 2 \cdot \frac{2A}{\pi}$

$\displaystyle a_0 = \frac{4A}{\pi}$

El valor de $a_n$ es

$\displaystyle c_n = \frac{1}{2} (a_n - j b_n)$

$\displaystyle 2c_n = a_n - j b_n$

$\displaystyle 2c_n - a_n = - jb_n$

$\displaystyle - 2c_n + a_n = jb_n$

$\displaystyle c_{-n} = c_n^* = \frac{1}{2} (a_n + j b_n)$

$\displaystyle 2c_{-n} = a_n + j b_n$

$\displaystyle 2c_{-n} - a_n = j b_n$

$\displaystyle - 2c_n + a_n = 2c_{-n} - a_n$

$\displaystyle 2a_n = 2c_{-n} + 2 c_{n}$

$\displaystyle a_n = c_{-n} + c_{n}$

$\displaystyle a_n = 2 \Re[c_n]$

$\displaystyle a_n = 2 \Re \left[ \frac{2A}{\pi (1 - 4n^2)} \right]$

$\displaystyle a_n = \frac{4A}{\pi (1 - 4n^2)}$

donde $\Re$ significa «parte real de » (algunos autores lo denotan como $Re$ ).

El valor de $b_n$ es

$\displaystyle c_n = \frac{1}{2} (a_n - j b_n)$

$\displaystyle 2c_n = a_n - j b_n$

$\displaystyle 2c_n + j b_n = a_n$

$\displaystyle c_{-n} = c_n^* = \frac{1}{2} (a_n + j b_n)$

$\displaystyle 2c_{-n} = a_n + j b_n$

$\displaystyle 2c_{-n} - j b_n = a_n$

$\displaystyle 2c_n + j b_n = 2c_{-n} - j b_n$

$\displaystyle 2 j b_n = 2c_{-n} - 2c_n$

$\displaystyle b_n = \frac{1}{j} c_{-n} - \frac{1}{j} c_n$

$\displaystyle b_n = - j c_{-n} + jc_n$

$\displaystyle b_n = jc_n - j c_{-n}$

$\displaystyle b_n = j(c_n - c_{-n}) = - 2 \Im[c_n]$

$\displaystyle b_n = - 2 \Im \left[ \frac{2A}{\pi (1 - 4n^2)} \right]$

$\displaystyle b_n = 2 (0)$

$\displaystyle b_n = 0$

donde $\Im$ significa «parte imaginaria de » (algunos autores lo denotan como $Im$ ).

Entonces, la serie trigonométrica de Fourier esperada es

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_0 t})}$

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \frac{2\pi}{T} t} + b_n \sin{n \frac{2\pi}{T} t})}$

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{2 n \pi t} + b_n \sin{2 \pi n t})}$

$\displaystyle f(t) = \frac{1}{2} \cdot \frac{4A}{\pi} + \sum_{n=1}^{\infty}{\left[ \frac{4A}{\pi (1 - 4n^2)} \cos{2 n \pi t} + (0) \sin{2 n \pi t} \right]}$