Introducción
Si una función periódica de período
llega a ser que
tienda a infinito, entonces esa función resultante
dejará de ser periódica, en base al procedimiento de límite mediante un tren de pulsos rectangulares.
Para conocer esto, se considera el tren de pulsos rectangulares que se muestra en la figura 1.

Figura 1a. 
Figura 1b. 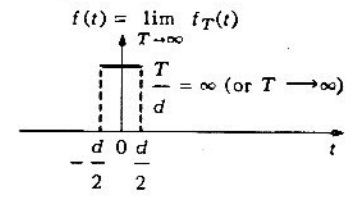
Figura 1c.
donde
Y también
,
Si , se obtiene la función (mostrado en la figura 1c)
Y esto es evidente que no es una función periódica.
Efectos al incrementar el período en el espectro de una función periódica
Ahora, utilizando el tren de pulsos rectangulares de la siguiente figura, se discutirá los efectos de incrementar el período en el espectro de la función periódica.
El espectro de frecuencia del pulso rectangular periódico [resuelto en el problema 1, del tema Espectros de frecuencia compleja. Fourier]. En la figura 2 (Espectros de amplitud para d=1/20 y T=1/4) y 3.3.3 (Espectro de amplitud para d=1/20, T=1/2) se ha observado que cuando el espectro discreto de una función periódica con período , se dibujó en función de la frecuencia, por lo que, la distancia entre armónicos adyascentes es la frecuencia fundamental
. De este modo, a medida que el período
aumenta,
disminuye y las líneas en el espectro se acercan unas a otras. En consecuencia, el número de líneas (armónicos) en una banda de frecuencia aumenta.
Por otra parte, del resultado obtenido del problema 1, Espectros de frecuencia compleja. Fourier, se tiene lo siguiente
Por tanto, si el período aumenta, las amplitudes de todos los armónicos disminuyen.
Esto se concluye que en el límite, a medida que se acerca al infinito, los armónicos se encuentran infinitamente cercanos y son de amplitud infinitesimal, es decir, el espectro discreto se vuelve continuo.
Representación de Fourier de una función f(t) no periódica
Sea una función períodica con período
, cuando
se aproxima a infinito,
se convierte en una función no períodica. Para encontrar la representación de Fourier de esa función no periódica, se empieza por la forma compleja de la serie de Fourier
– – – (1)
donde
– – – (2)
– – – (3)
Sustituyendo (2) en (1)
Tomando como la variable comodín dentro de la integral para evitar confunsión con
– – – (4)
con motivo de no involucrar el término de la exponencial de la suma con los términos de la integral. Ahora, la ecuación (4) también se puede expresar como
– – – (5)
En el caso de la ecuación (3), haciendo que tienda a infinito
Ahora, sea ; entonces, la frecuencia de cualquier armónico
debe corresponder a la variable general de frecuencia que describe el espectro continuo. En otras palabras, si
tiende a infinito a medida que
tienda a cero, el producto es finito, esto es
Así que, de la ecuación (5)
Tomando el límite en ambos miembros, cuando tienda a infinito
– – – (6)
Definiendo
– – – (7)
la ecuación (6) se convierte en
– – – (8)
Por tanto, las ecuaciones (7) y (8) son la representación de Fourier de la función no periódica.
Se observa que la ecuación (7) es análoga a (1), y la ecuación (8) es análoga a (2). La relación que se muestra en la ecuación (6) se conoce como identidad de Fourier.
Integral de Fourier
Teorema 1. El teorema de la integral de Fourier afirma que si es real, entonces
Demostración del teorema 1. De la ecuación (6)
también se puede expresar como
– – – (9)
Por identidad de Euler [], se tiene
Tomando sólo la parte real, provocará que sea real Entonces
Como la función es par con respecto a
Y el teorema queda demostrado.