Transformada de Fourier. Fourier

Introducción

La función $F(\omega)$ definida por

$\displaystyle F (\omega) = \int_{-\infty}^{\infty}{f(t) e^{-j \omega \, t} \, dt}$

– – – (1)

se conoce como la integral de Fourier o la transformada de Fourier de $f(t)$ , y la operación de integración simbólica frecuentemente por $\mathcal{F}$ ; esto es

$\displaystyle F (\omega) = \mathcal{F} [f(t)]= \int_{-\infty}^{\infty}{f(t) e^{-j \omega \, t} \, dt}$

– – – (2)

Análogamente $\mathcal{F}^{-1}$ es el símbolo que se utiliza para indicar la operación inversa, es decir, para obtener $f(t)$ cuando $F(\omega)$ está dado; esto es,

$\displaystyle f(t) = \mathcal{F}^{-1}[F(\omega)] = \frac{1}{2\pi} \int_{-\infty}^{\infty}{F(\omega) e^{j \omega \, t} \, d\omega}$

– – – (3)

y $f(t)$ se denomina transformada inversa de Fourier de $F(\omega)$ . Las ecuaciones (2) y (3) se conocen a menudo como par de transformadas de Fourier. La condición para que exista $F(\omega)$ generalmente está dada por

$\displaystyle \int_{-\infty}^{\infty}{|f(t)| \, dt} < \infty$

– – – (4)

En otros términos, la integral del valor absoluto de $f(t)$ debe ser finita.

Nota. Se debe observa que la ecuación (4) es una condición suficiente pero no necesaria para la existencia de $\mathcal{F}[f(t)]$ ; las funciones que no satisfacen a la ecuación (4) pueden tener transformadas de Fourier.

La función $F(\omega) = \mathcal{F}[f(t)]$ es, en general, compleja y, se tiene

$F(\omega) = R(\omega) + j X(\omega) = |F(\omega)| e^{j \phi(\omega)}$

donde $|F(\omega)|$ se denomina espectro de magnitud de $f(t)$ , y $\phi(\omega)$ , espectro de fase de $f(t)$ .

Teoremas y demostraciones

Teorema 1. Si $f(t)$ es real, las partes real e imaginaria de $F(\omega)$ son

$\displaystyle R(\omega) = \int_{-\infty}^{\infty}{f(t) \cos{\omega t} \, dt}$

$\displaystyle X(\omega) = - \int_{-\infty}^{\infty}{f(t) \sin{\omega t} \, dt}$

Así mismo $R(\omega)$ y $X(\omega)$ son funciones par e impar de $\omega$ , respectivamente; es decir,

$R(\omega) = R(-\omega)$

$X(\omega) = - X(-\omega)$

$F(-\omega) = F^*(\omega)$

donde $F^*(\omega)$ denota el conjugado complejo de $F(\omega)$ .

Demostración del teorema 1. Partiendo de la ecuación

$\displaystyle F (\omega) = \int_{-\infty}^{\infty}{f(t) e^{-j \omega \, t} \, dt}$

Utilizando la idéntidad de Euler

$e^{-j \omega \, t} = \cos{\omega t} - j\sin{\omega t}$

La ecuacion tiene la siguiente expresión

$\displaystyle F (\omega) = \int_{-\infty}^{\infty}{f(t) (\cos{\omega t} - j\sin{\omega t}) \, dt}$

$\displaystyle F(\omega) = \int_{-\infty}^{\infty}{f(t) \cos{\omega t} \, dt} - j\int_{-\infty}^{\infty}{f(t) \sin{\omega t} \, dt}$

$F(\omega) = R(\omega) + j X(\omega)$

Igualando las partes real e imaginaria

$\displaystyle R (\omega) = \int_{-\infty}^{\infty}{f(t) \cos{\omega t} \, dt}$

$\displaystyle X(\omega) = - \int_{-\infty}^{\infty}{f(t) \sin{\omega t} \, dt}$

Y estos son la parte real y parte imaginaria de $F(\omega)$ , del teorema 1, si $f(t)$ es real. Ahora se observará que $R(\omega)$ es par y $X(\omega)$ es imaginaria. Para $R(\omega)$

$\displaystyle R (\omega) = \int_{-\infty}^{\infty}{f(t) \cos{\omega t} \, dt}$

$\displaystyle R (-\omega) = \int_{-\infty}^{\infty}{f(t) \cos{(-\omega t)} \, dt}$

$\displaystyle R (-\omega) = \int_{-\infty}^{\infty}{f(t) \cos{\omega t} \, dt}$

$\displaystyle R (\omega) = R(-\omega)$

Esto queda demostrado que $R (\omega)$ es par. Y para $X(\omega)$

$\displaystyle X(\omega) = - \int_{-\infty}^{\infty}{f(t) \sin{\omega t} \, dt}$

$\displaystyle X(-\omega) = - \int_{-\infty}^{\infty}{f(t) \sin{(-\omega t)} \, dt}$

$\displaystyle X(\omega) = - \left[- \int_{-\infty}^{\infty}{f(t) \sin{\omega t} \, dt} \right]$

$\displaystyle X(\omega) = - X(-\omega)$

O también

$\displaystyle X(-\omega) = - X(\omega)$

Esto queda demostrado que $X (\omega)$ es impar. Por último

$F(\omega) = R(\omega) + j X(\omega)$

$F(-\omega) = R(-\omega) + j X(-\omega)$

$F(-\omega) = R(\omega) - j X(\omega)$

$F(-\omega) = F^*(\omega)$

Y esto queda demostrado.

Teorema 2. La ecuación $F(-\omega) = F^*(\omega)$ es condición necesaria y suficiente para que $f(t)$ sea real.

Demostración del teorema 2. Sea

$f(t) = f_1 (t) + jf_2(t)$

donde $f_1(t)$ y $f_2 (t)$ son funciones reales. Luego

$f(t) = f_1 (t) + jf_2(t)$

$\displaystyle \frac{1}{2\pi} \int_{-\infty}^{\infty}{f(t) \, e^{j \omega t} \, dt} = f_1 (t) + jf_2(t)$

$\displaystyle \frac{1}{2\pi} \int_{-\infty}^{\infty}{[R(\omega) + j X(\omega)] \, (\cos{\omega t} + j\sin{\omega t} \, dt} = f_1 (t) + jf_2(t)$

$\displaystyle \frac{1}{2\pi} \int_{-\infty}^{\infty}{[R(\omega) \cos{\omega t} + j X(\omega) \cos{\omega t} + j R(\omega t) \sin{\omega t} - R(\omega) \cos{\omega t}] \, dt} = f_1 (t) + jf_2(t)$

$\displaystyle \frac{1}{2\pi} \int_{-\infty}^{\infty}{[R(\omega) \cos{\omega t} - X(\omega) \sin{\omega t}] \, dt} + j\frac{1}{2\pi} \int_{-\infty}^{\infty}{[R(\omega) \sin{\omega t} + X(\omega) \cos{\omega t}] \, dt} = f_1 (t) + jf_2(t)$

$\displaystyle f_1 (t) + jf_2(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty}{[R(\omega) \cos{\omega t} - X(\omega) \sin{\omega t}] \, dt} + j\frac{1}{2\pi} \int_{-\infty}^{\infty}{[R(\omega) \sin{\omega t} + X(\omega) \cos{\omega t}] \, dt}$

$\displaystyle f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty}{[R(\omega) \cos{\omega t} - X(\omega) \sin{\omega t}] \, dt} + j\frac{1}{2\pi} \int_{-\infty}^{\infty}{[R(\omega) \sin{\omega t} + X(\omega) \cos{\omega t}] \, dt}$

Por el método de igualación se observa que

$\displaystyle \frac{1}{2\pi} \int_{-\infty}^{\infty}{[R(\omega) \cos{\omega t} - X(\omega) \sin{\omega t}] \, dt} = f_1 (t)$

$\displaystyle \frac{1}{2\pi} \int_{-\infty}^{\infty}{[R(\omega) \sin{\omega t} + X(\omega) \cos{\omega t}] \, dt} = f_2(t)$

Ahora, si $F(-\omega) = F^*(\omega)$ , entonces

$R(-\omega) = R(\omega)$

$X(- \omega) = - X(\omega)$

En consecuencia

$R(- \omega) \sin{(- \omega t)} = - R(\omega) \sin{\omega t}$

$R (- \omega) \cos{(- \omega t)} = R(\omega) \cos{\omega t}$

$X(-\omega) \sin{(- \omega t)} = [-X(\omega)] [- \sin{\omega t}] = X(\omega) \sin{\omega t}$

$X(- \omega) \cos{(- \omega t)} = [-X(\omega)] \cos{\omega t} = - X(\omega) \cos{\omega t}$

Por lo que $R(\omega) \sin{\omega t}$ y $X(\omega) \cos{\omega t}$ son funciones impares de $\omega$ mientras que $R(\omega) \cos{\omega t}$ y $X(\omega) \sin{\omega t}$ son funciones pares de $\omega$ , y el integrando

es una función impar de $\omega$ . Por consiguiente

$\displaystyle f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty}{R(\omega) \cos{\omega t} \, dt} - \frac{1}{2\pi} \int_{-\infty}^{\infty}{X(\omega) \sin{\omega t} \, dt} + j\frac{1}{2\pi} \int_{-\infty}^{\infty}{R(\omega) \sin{\omega t} \, dt} + j\frac{1}{2\pi} \int_{-\infty}^{\infty}{X(\omega) \cos{\omega t} \, dt}$

$\displaystyle f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty}{R(\omega) \cos{\omega t} \, dt} - \frac{1}{2\pi} \int_{-\infty}^{\infty}{X(\omega) \sin{\omega t} \, dt} + j0 + j0$

$\displaystyle f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty}{R(\omega) \cos{\omega t} \, dt} - \frac{1}{2\pi} \int_{-\infty}^{\infty}{X(\omega) \sin{\omega t} \, dt} + j0$

se tiene que $f_2 (t) = 0$ , es decir, $f(t)$ es real. Por tanto, se concluye que la ecuación $F(-\omega) = F^*(\omega)$ es condición necesaria y suficiente para que $f(t)$ sea real.

Teorema 3. Si $f(t)$ es real, su espectro de magnitud $|F(\omega)|$ es una función par de $\omega$ , y que su espectro de fase $\phi (\omega)$ es una función impar de $\omega$ .

Demostración del teorema 3. Si $f(t)$ es real, entonces

$F(-\omega) = F^*(\omega)$

Recordando que

$\displaystyle F(\omega) = |F(\omega)| e^{j \phi(\omega)}$

Tambien se tiene que

$\displaystyle F(- \omega) = |F(- \omega)| e^{j \phi(-\omega)}$

$\displaystyle F^*(\omega) = |F(\omega)| e^{- j \phi(\omega)}$

Después

$F(-\omega) = F^*(\omega)$

$|F(- \omega)| e^{j \phi(-\omega)} = |F(\omega)| e^{-j \phi(\omega)}$

Por el método de igualación, se concluye que

$|F(-\omega)| = |F(\omega)|$

$\phi(-\omega) = - \phi(\omega)$

es decir, el espectro de magnitud $|F(\omega)|$ es una función par de $\omega$ y el su espectro de fase $\phi (\omega)$ es una función impar de $\omega$ .

Teorema 4. Si la transformada de Fourier de una función real $f(t)$ es real, entonces $f(t)$ es una función par de $t$ , y que si la transformada de Fourier de una función real $f(t)$ es imaginaria pura, entonces $f(t)$ es una función impar de $t$ .

Demostración del teorema 4. Sea

$\mathcal{F}[f(t)] = F(\omega) = R(\omega) + jX(\omega)$

Recordando que

$\displaystyle R(\omega) = \int_{-\infty}^{\infty}{f(t) \cos{\omega t} \, dt}$

$\displaystyle X(\omega) = - \int_{-\infty}^{\infty}{f(t) \sin{\omega t} \, dt}$

Si $F(\omega) = R(\omega)$ y $X(\omega) = 0$ , entonces

$\displaystyle X(\omega) = - \int_{-\infty}^{\infty}{f(t) \sin{\omega t} \, dt}$

debe ser impar con respecto a $t$ . Puesto que $\sin{\omega t}$ es una función impar de $t$ , $f(t)$ debe de ser una función par de $t$ .

Problemas resueltos

Problema 1. Encontrar la transformada de Fourier del pulso rectangular $p_d (t)$ definido por

$\displaystyle p_d (t) = \left\{ \begin{matrix} 1, \quad |t| < \frac{1}{2} d \\0, \quad |t|> \frac{1}{2} d \end{matrix} \right.$

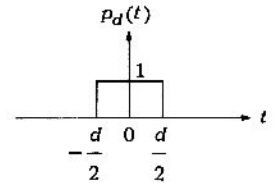
Figura 4.2.1 Pulso rectangular del problema 1 — *Figura 1. Pulso rectangular del problema 1.*

Solución.

$\displaystyle f(t) = p_d (t)$

$\displaystyle \mathcal{F}[f(t)] = \mathcal{F}[p_d (t)]$

$\displaystyle F(\omega) = \int_{-\infty}^{\infty}{p_d (t) e^{-j \omega t} \, dt}$

$\displaystyle F(\omega) = \int_{-d/2}^{d/2}{(1) e^{-j \omega t} \, dt} = \int_{-d/2}^{d/2}{e^{-j \omega t} \, dt}$

$\displaystyle F (\omega) = \left[-\frac{1}{j \omega} e^{-j \omega t} \right]_{-d/2}^{d/2}$

$\displaystyle F (\omega) = \left[-\frac{1}{j \omega} e^{-j \omega d/2} + \frac{1}{j \omega} e^{-j \omega (-d/2)} \right]$

$\displaystyle F (\omega) = \left[-\frac{1}{j \omega} e^{-j \omega d/2} + \frac{1}{j \omega} e^{j \omega d/2} \right]$

$\displaystyle F (\omega) = \frac{1}{j \omega} \left(- e^{-j \omega d/2} + e^{j \omega d/2} \right)$

$\displaystyle F (\omega) = \frac{1}{j \omega} \left(e^{j \omega d/2} - e^{-j \omega d/2} \right)$

$\displaystyle F (\omega) = \frac{1}{\omega} \left(\frac{e^{j \omega d/2} - e^{-j \omega d/2}}{j} \right)$

$\displaystyle F (\omega) = \frac{1}{\omega} \frac{2}{2} \left(\frac{e^{j \omega d/2} - e^{-j \omega d/2}}{j} \right)$

$\displaystyle F (\omega) = \frac{2}{\omega} \left(\frac{e^{j \omega d/2} - e^{-j \omega d/2}}{2j} \right)$

$\displaystyle F (\omega) = \frac{2}{\omega} \sin{\left(\frac{\omega d}{2} \right)}$

$\displaystyle F (\omega) = \frac{2}{\omega} \cdot \frac{\frac{\omega d}{2}}{\frac{\omega d}{2}} \cdot \sin{\left(\frac{\omega d}{2} \right)}$

$\displaystyle F (\omega) = \frac{2}{\omega} \cdot \frac{\omega d}{2} \cdot \frac{\sin{\left(\frac{\omega d}{2} \right)}}{\frac{\omega d}{2}}$

$\displaystyle F (\omega) = d \cdot \frac{\sin{\left(\frac{\omega d}{2} \right)}}{\frac{\omega d}{2}}$

Finalmente

$\displaystyle \therefore F(\omega) = d \cdot \frac{\sin{\left(\frac{\omega d}{2} \right)}}{\frac{\omega d}{2}}$

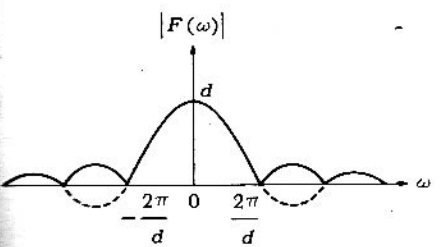
Figura 4.2.2 La transformada de Fourier del pulso rectangular del problema 1 — *Figura 2. Transformada de Fourier del pulso rectangular del problema 1.*

Problema 2. Encontrar la transformada de Fourier de $f(t)$ definida por

$\displaystyle f (t) = \left\{ \begin{matrix} e^{-\alpha t}, & t > 0 \\0, & t < 0 \end{matrix} \right.$

donde $\alpha > 0$ .

Figura 4.2.3 Funcion f(t) del problema 2 — *Figura 3. Función f(t) del problema 2.*

Solución.

$\displaystyle f(t) = f (t)$

$\displaystyle \mathcal{F}[f(t)] = \mathcal{F}[f(t)]$

$\displaystyle F(\omega) = \int_{-\infty}^{\infty}{f (t) e^{-j \omega t} \, dt}$

$\displaystyle F(\omega) = \int_{0}^{\infty}{e^{-\alpha t} e^{-j \omega t} \, dt} = \int_{0}^{\infty}{e^{-(\alpha + j\omega) t} \, dt}$

$\displaystyle F(\omega) = \left[- \frac{1}{\alpha + j\omega} e^{-(\alpha + j\omega) t} \right]_{0}^{\infty}$

$\displaystyle F(\omega) = \left[- \frac{1}{\alpha + j\omega} e^{-(\alpha + j\omega) \infty} + \frac{1}{\alpha + j\omega} e^{-(\alpha + j\omega) (0)} \right]$

$\displaystyle F(\omega) = \left[- \frac{1}{\alpha + j\omega} (0) + \frac{1}{\alpha + j\omega} (1) \right]$

$\displaystyle F(\omega) = \left(0 + \frac{1}{\alpha + j\omega} \right)$

$\displaystyle F(\omega) = \frac{1}{\alpha + j\omega}$

Finalmente

$\displaystyle \therefore F(\omega) = \frac{1}{\alpha + j\omega}$

Un comentario sobre “Transformada de Fourier. Fourier”

Nolan Bute dice:

31 marzo, 2019 a las 7:16 am

My spouse and i ended up being really fortunate Peter managed to finish up his research by way of the ideas he gained using your web page. It is now and again perplexing to simply continually be offering ideas that many many people have been making money from. And we all understand we have you to give thanks to for this. These illustrations you’ve made, the simple site navigation, the friendships you will make it easier to promote – it is everything amazing, and it’s making our son and the family reason why that article is awesome, and that’s particularly fundamental. Thank you for everything!

Me gustaMe gusta

Responder