Propiedades de las transformadas de Fourier. Fourier.

Teoremas

Teorema 1. Propiedad de linealidad. Si $F_1 (\omega) = \mathcal{F}[f_1 (t)]$ y $F_2 (\omega) = \mathcal{F}[f_2 (t)]$ , y $a_1$ y $a_2$ son dos constantes arbitrarias, entonces

$\displaystyle \mathcal{F}[a_1 f_1(t) + a_2 f_2 (t)] = a_1 F_1(\omega) + a_2 F_2 (\omega)$

Teorema 2. Propiedad de escalonamiento. Si $a_1$ es una constante real y $F(\omega) = \mathcal{F}[f(t)]$ , entonces

$\displaystyle \mathcal{F}[f(at)] = \frac{1}{|a|} F \left(\frac{\omega}{a} \right)$

Teorema 3. Si $\mathcal{F}[f(t)] = F(\omega)$ , entonces

$\mathcal{F}[f(-t)] = F(-\omega)$

Teorema 4. Propiedad de desplazamiento en el tiempo. Si $\mathcal{F}[f(t)] = F(\omega)$ , entonces

$\mathcal{F}[f(t-t_0)] = F(\omega) e^{-j\omega t_0}$

Teorema 5. Propiedad de desplazamiento en la frecuencia. Si $\omega_0$ es una constante real y $\mathcal{F}[f(t)] = F(\omega)$ , entonces

$\mathcal{F}[f(t)e^{j\omega_0 t}] = F(\omega - \omega_0)$

Teorema 6. Propiedad de simetría. Si $F(\omega) = \mathcal{F}[f(t)]$ , entonces

$\mathcal{F} [F(t)] = 2\pi f(-\omega)$

Teorema 7. Si $\mathcal{F}[f(t)] = F(\omega)$ y $f(t) \rightarrow 0$ cuando $t \rightarrow \pm \infty$ , entonces

$\mathcal{f'(t)} = j\omega F(\omega) = j\omega \mathcal{F}[f(t)]$

Este teorema muestra la diferenciación en el dominio del tiempoque corresponde a la multiplicación de la transformada de Fourier por $j\omega$ dado que $f(t) \rightarrow 0$ cuando $t \rightarrow \pm \infty$ .

Se observa que si $f(t)$ tiene un número finito de súbitas discontinuidades, entonces $f'(t)$ contiene impulsos. Por consiguiente, la transformada de Fourier de $f'(t)$ , en este caso, debe contener transformada de Fourier de los impulsos de $f'(t)$ .

Mediante la aplicación repetida del teorema 7,

$\displaystyle \mathcal{F}[f^n (t)] = (j\omega)^n F(\omega) = (j \omega) \mathcal{F} [f(t)]$ , $n=1,2, \cdots$

Teorema 8. Si $\mathcal{F}[f(t)] = F(\omega)$ , $\omega \ne 0$ , y

$\displaystyle \int_{-\infty}^{\infty}{f(t) \, dt} = F(0) = 0$ ,

entonces,

$\displaystyle \mathcal{F} \left[\int_{-\infty}^{t}{f(x) \, dx} \right] = \frac{1}{j\omega} F(\omega) = \frac{1}{j\omega} \mathcal{F}[f(t)]$

Teorema 9. Si $\mathcal{F}[f(t)] = F(\omega)$ , $\omega = 0$ , entonces

$\displaystyle \mathcal{F}[\phi(t)] = \int_{- \infty}^{\infty}{\phi (t) \, dt}$

Cuando $\displaystyle F(0) = \int_{-\infty}^{\infty}{f(x) \, dx} \ne 0$ , se tiene

$\displaystyle \mathcal{F} \left[ \int_{-\infty}^{t}{f(x) \, dx} \right] = \frac{1}{j\omega} F(\omega) + \pi \, F(0) \, \delta(\omega)$

Teorema 10. Si $\mathcal{F} [f(t)] = F(\omega)$ , entonces

$\displaystyle \mathcal{F}[-jt \, f(t)] = \frac{d}{d\omega} [F(\omega)]$

Problemas resueltos

Problema 1. Si $F(\omega) = \mathcal{F}[f(t)]$ , hallar la transformada de Fourier de $f(t) \cos{\omega_0 t}$ .

Solución.

$F(\omega) = \mathcal{F}[f(t) \cos{\omega_0 t}]$

$\displaystyle F(\omega) = \mathcal{F} \left[f(t) \left(\frac{e^{j \omega_0 t} + e^{-j \omega_0 t}}{2} \right) \right]$

$\displaystyle F(\omega) = \frac{1}{2} \mathcal{F} \left[f(t) \left(e^{j \omega_0 t} + e^{-j \omega_0 t} \right) \right]$

$\displaystyle F(\omega) = \frac{1}{2} \mathcal{F} \left[f(t) e^{j \omega_0 t} + f(t) e^{-j \omega_0 t} \right]$

$\displaystyle F(\omega) = \frac{1}{2} \mathcal{F} \left[f(t) e^{j \omega_0 t} \right] + \frac{1}{2} \mathcal{F} \left[f(t) e^{-j \omega_0 t} \right]$

$\displaystyle \therefore F(\omega) = \frac{1}{2} F(\omega - \omega_0) + \frac{1}{2} F(\omega + \omega_0)$

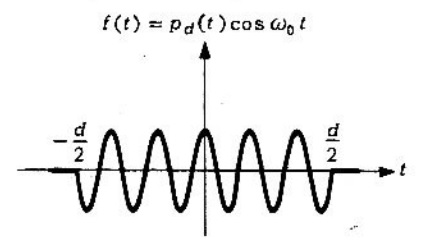
Problema 2. Hallar la transformada de Fourier de la función coseno de duración finita igual a $d$ .

Solución. La función coseno de duración $d$ se puede expresar como una función modulada por pulso; es decir,

$f(t) = p_d(t) \cos{\omega_0 t}$ ,

donde

$\displaystyle p_d (t) = \left\{ \begin{matrix} 1, \quad |t| < \frac{1}{2} d \\ 0, \quad |t| > \frac{1}{2} d \end{matrix} \right.$

Figura 4.5.1 Funcion coseno de duración finita — *Figura 1. Función coseno de duración finita.*

Determinando la transformada de Fourier

$\displaystyle F(\omega) = \mathcal{F} [f(t)]$

$\displaystyle F(\omega) = \mathcal{F} [p_d(t) \cos{\omega_0 t}]$ ,

$\displaystyle F(\omega) = \mathcal{F} \left[p_d(t) \left(\frac{e^{j \omega_0 t} - e^{j \omega_0 t}}{2} \right) \right]$

$\displaystyle F(\omega) = \frac{1}{2} \mathcal{F} \left[p_d(t) \left(e^{j \omega_0 t} - e^{-j \omega_0 t} \right) \right]$

$\displaystyle F(\omega) = \frac{1}{2} \mathcal{F} \left[p_d(t) e^{j \omega_0 t} \right] - \frac{1}{2} \mathcal{F} \left[p_d(t) e^{-j \omega_0 t} \right]$

Recordando que

$\displaystyle \mathcal{F} [p_d(t)] = \frac{2}{\omega} \sin{\left(\frac{\omega d}{2} \right)}$

Por la propiedad de desplazamiento de la frecuencia, se observa que

$\displaystyle F(\omega) = \frac{1}{2} \mathcal{F} \left[p_d(t) e^{j \omega_0 t} \right] + \frac{1}{2} \mathcal{F} \left[p_d(t) e^{-j \omega_0 t} \right]$

$\displaystyle F(\omega) = \frac{1}{2} \cdot \left(\frac{2}{\omega - \omega_0} \right) \sin{\left[\frac{(\omega - \omega_0) d}{2} \right]} + \frac{1}{2} \cdot \left(\frac{2}{\omega + \omega_0} \right) \sin{\left[\frac{(\omega + \omega_0) d}{2} \right]}$

$\displaystyle F(\omega) = \left(\frac{1}{\omega - \omega_0} \right) \sin{\left[\frac{(\omega - \omega_0) d}{2} \right]} + \left(\frac{1}{\omega + \omega_0} \right) \sin{\left[\frac{(\omega + \omega_0) d}{2} \right]}$

El resultado de la transformada de Fourier, se muestra en la siguiente figura.

Figura 4.5.2 Transformada de Fourier de la funcion coseno — *Figura 2. Transformada de Fourier de la función coseno.*

Problema 3. Hallar la transformada de Fourier de la función

$\displaystyle f(t) = \frac{\sin{at}}{\pi t}$

Solución. Recordando que

$\displaystyle \mathcal{F} [p_d(t)] = \frac{2}{\omega} \sin{\left(\frac{\omega d}{2} \right)}$

Por la propiedad de simetría, se observa que

$\displaystyle \mathcal{F} \left[ \frac{2}{t} \sin{\left(\frac{t d}{2} \right)} \right] = 2\pi p_d (-\omega)$

$\displaystyle \frac{1}{2\pi} \mathcal{F} \left[ \frac{2}{t} \sin{\left(\frac{t d}{2} \right)} \right] = p_d (-\omega)$

$\displaystyle \mathcal{F} \left[ \frac{2}{2\pi t} \sin{\left(\frac{t d}{2} \right)} \right] = p_d (-\omega)$

$\displaystyle \mathcal{F} \left[ \frac{1}{\pi t} \sin{\left(\frac{t d}{2} \right)} \right] = p_d (-\omega)$

$\displaystyle \mathcal{F} \left[ \frac{1}{\pi t} \sin{\left(\frac{d}{2} t \right)} \right] = p_d (-\omega)$

También se recuerda que $p_d (\omega)$ está definida como

$\displaystyle p_d (\omega) = \left\{ \begin{matrix} 1, \quad |\omega| < \frac{1}{2} d \\0, \quad |\omega|> \frac{1}{2} d \end{matrix} \right.$

es una función par de $\omega$ ; por consiguiente

$p_d (-\omega) = p_d (\omega)$

Asignando a $a=\frac{1}{2}d$ (como también $d=2a$ ), se tiene lo siguiente

$\displaystyle \mathcal{F} \left[ \frac{1}{\pi t} \sin{\left(\frac{d}{2} t \right)} \right] = p_d (-\omega)$

$\displaystyle \mathcal{F} \left[ \frac{1}{\pi t} \sin{\left(a t \right)} \right] = p_{2a} (-\omega)$

donde

$\displaystyle p_{2a} (\omega) = \left\{ \begin{matrix} 1, \quad |\omega| < a \\0, \quad |\omega|> a \end{matrix} \right.$

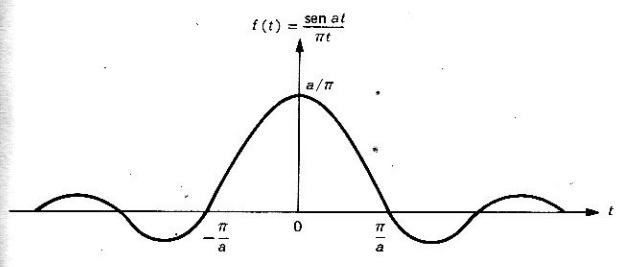
Las gráficas de $f(t) = \sin(at) / \pi t$ y su transformada, $F(\omega)$ , se muestran en las siguientes figuras.

Propiedades de las transformadas de Fourier. Fourier.

Teoremas

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Propiedades de las transformadas de Fourier. Fourier.

Teoremas

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta