Introducción
De la siguiente figura, se obtendrá la transformada de Fourier de una función constante (asignado como ).
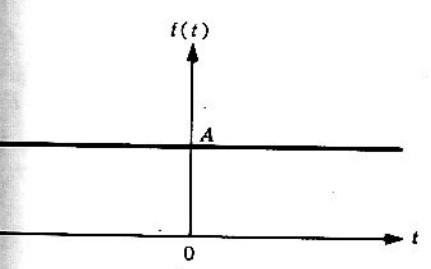
Partiendo de
Aplicando la transformada de Fourier en ambos miembros
Continuando
Recordando la expresión general de la función impulso unitario es
Se asigna a y a
, por lo que, la expresión anterior queda de la siguiente manera
Regresando y sustituyendo
Se sabe que
Entonces
o

Si , entonces
Transformada de Fourier de una función exponencial
Como y
, se observa que
Transformada de Fourier de la función seno
Aplicando la identidad del seno
Aplicando la transformada de Fourier en ambos miembros
Finalmente
Transformada de Fourier de la función coseno
Aplicando la identidad del coseno
Aplicando la transformada de Fourier en ambos miembros
Finalmente
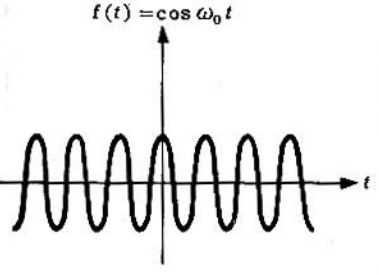
Figura 3. La función coseno. 
Figura 4. Transformada de Fourier de la función coseno.
Hay un error en la Transformada de Fourier de la función seno al reemplazar e^-iw_0t, su transformada es 2.pi.delta(w+w_0)
Me gustaMe gusta
Gracias por la observación. Ya se corrigió; hubo un error de dedo.
Me gustaMe gusta