Problema. El eje de un motor gira a una velocidad de 1800 r/min. ¿Cuál es la velocidad del eje en radianes por segundo?

Solución. Realizando la conversión

\displaystyle \omega = 1800 \ \mbox{rev/min}

\displaystyle \omega = 1800 \ \mbox{rev/min} \left( \frac{2\pi \mbox{rad}}{1 \ \mbox{rev}} \right) \left( \frac{1 \ \mbox{min}}{60 \ \mbox{seg}} \right)

\displaystyle \mathbf{ \omega = 188.5 \ (\mbox{rad/seg})}

Problema. Un volante cuyo momento de inercia es de 4 kg \cdot m^2 está inicialmente en reposo. Si se le aplica de manera repentina un par de 6 N \cdot m (en sentido contrario a las manecillas del reloj), ¿Cuál será la velocidad del volante después de 5 segundos? Exprese esta velocidad en radianes por segundo y revoluciones por minuto (rpm o rev/min).

Solución. Tomando la fórmula de la velocidad angular

\omega = \alpha \cdot t

 Y recordando que \displaystyle \alpha = \frac{\tau}{\mathcal{J}}, se sustituye los siguiente

\omega = \alpha \cdot t

\displaystyle \omega = \frac{\tau}{\mathcal{J}} \cdot t

\displaystyle \omega = \frac{6 \ N \cdot m}{4 \ kg \cdot m^2} (5 \ \mbox{seg})

\displaystyle \therefore \omega = 7.5 \frac{rad}{seg}

La aceleración angular está expresado en radianes por segundo, para convertirlos a revoluciones por minutos, se lleva a cabo la siguiente conversión

\displaystyle \omega = 7.5 \frac{rad}{seg}

\displaystyle \omega = 7.5 \frac{rad}{seg} \left(\frac{1 \ rev}{2\pi \ rad} \right) \left(\frac{60 \ seg}{1 \ min} \right)

\displaystyle \therefore \mathbf{\omega = 71.62 \frac{rev}{min}}

Problema. Una fuerza de 10 N se aplica a un cilindro de radio r=0.15 \ m, como se muestra en la figura. El momento de inercia de este cilindro es de \mathcal{J}=4 \ kg \cdot m^2. ¿Cuál es la magnitud y cuál es la dirección del par producido en el cilindro? ¿Cuál es la aceleración angular \alpha del cilindro?

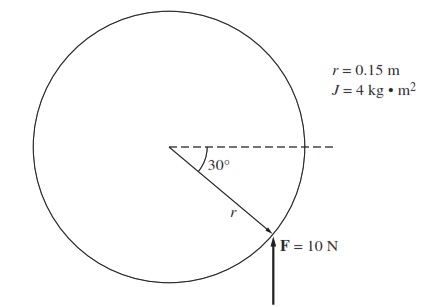
Figura P1. Cilindro del enunciado 3.
Figura 1.1.1 Cilindro del enunciado 3.

Solución. La magnitud y dirección del troque producido por el cilindro es

\tau_{ind} = rF \sin{\theta}

= (0.15 \ m)(10 \ N) \sin{30}

\tau_{ind} = 0.75 \ N \cdot m (en sentido antihorario)

Por tanto, el valor de la aceleración angular del cilindro se obtiene al despejar la ecuación del torque.

\displaystyle \tau = \mathcal{J} \alpha

\displaystyle \alpha = \frac{\alpha}{\mathcal{J}}

Sustituyendo

\displaystyle \alpha = \frac{0.75 \ N \cdot m}{4 \ kg \cdot m^2}

\displaystyle \therefore \mathbf{\alpha = 0.1875 \left(\frac{rad}{s^2} \right) \approx 0.19 \left(\frac{rad}{s^2} \right)}

Problema. Un motor suministra a su carga un par de 50 N \cdot m. Si el eje del motor gira a 1500 r/min, ¿cuál es la potencia mecánica suministrada a la carga en watts? ¿Y en caballos de fuerza?

Solución. Tomando la fórmula de la potencia mecánica

P = \tau \omega

Sustituyendo y aplicando la conversión para obtener el resultado en Watts (W)

\displaystyle P = \left(50 \ N \cdot m \right) \left(1500 \frac{rev}{min} \right) \left( \frac{1 \ min}{60 \ seg} \right) \left(\frac{2\pi \ rad}{1 \ rev} \right)

\therefore \mathbf{P = 2500 \pi \ W = 7854 \ W}

Convirtiendo el último resultado en caballos de fuerza (Hp)

\displaystyle P = 7854 \ W \left( \frac{1 Hp}{746 \ W} \right)

\displaystyle \therefore \mathbf{P = 10.53 \ Hp}

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Un comentario sobre “Movimiento rotatorio, ley de Newton y relaciones de potencia. Problema 1. Máquinas eléctricas.”

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.