Problema 3. En la figura 1.1.4 se muestra un núcleo de dos columnas. La bobina dispuesta en la parte izquierda (N_1) tiene 600 vueltas y la bobina de la parte derecha (N_2) tiene 200 vueltas. Las bobinas están enrolladas en las direcciones que se muestran en la figura. Si se toma en cuenta las dimensiones que se aprecian en la figura, ¿qué flujo producirá las corrientes i_1 = 0.5 \ A e i_2 = 1.00 \ A? Se va a suponer que \mu_r = 1200 y es constante.

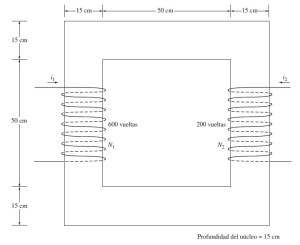
Figura 1.1.4 Núcleo ferromagnético del problema 3 de circuitos magnéticos.

Solución. Se determina la longitud total del núcleo ferromagnético.

l = 7.5 + 50 + 7.5 + 7.5 + 50 + 7.5 + 7.5 + 50 + 7.5 + 7.5 + 50 + 7.5

l = 260 (cm) = 2.6 m

Calculando el área de la sección transversal

A = (0.15 \ m)(0.15 \ m)

A = 0.0225 \ m^2

Después, se calcula la reluctancia total

\displaystyle \mathcal{R} = \frac{l}{\mu \ A}

\displaystyle \mathcal{R} = \frac{l}{\mu_r \ \mu_0 \ A} = \frac{2.6 \ m}{(1200)(4\pi \times 10^{-7} H/m)(0.0225 \ m^2)}

\displaystyle \mathcal{R} = 76,629.98 \ (A \cdot espiras / Wb) = 76.63 \times 10^3 (A \cdot espiras / Wb)

\displaystyle \mathcal{R} = 76.63 (kA \cdot espiras / Wb)

Por último, se determina el flujo total del núcleo

\mathcal{F} = \phi \mathcal{R}

\displaystyle \phi = \frac{\mathcal{F}}{\mathcal{R}} = \frac{N_1 i_1 + N_2 i_2}{\mathcal{R}}

\displaystyle \phi = \frac{(600 \ espiras)(0.5 \ A) + (200 \ espiras)(1 \ A)}{76.63 \times 10^{3} (A \cdot espiras / Wb)}

\therefore \phi = 6.52 \times 10^{-3} (Wb) = 6.52 \ mWb

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

6 comentarios sobre “Circuitos magnéticos. Problema 3. Máquinas eléctricas.”

  3. En la formula de la reluctancia total, el área lo tienes como 0.0225, pero ahí solo esta contando el área de un lado del núcleo, tendría que ser el área total que hay, no?.

    Me gusta

    Responder

Replica a Marvil Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.