Circuitos magnéticos. Problema 7. Máquinas eléctricas.

Problema 7.

En la figura 1 se muestra un núcleo magnético de dos columnas con entrehierro. La profundidad del núcleo es de 5 (cm), la longitud del entrehierro es de 0.05 (cm) y la bobina tiene 1000 vueltas. La curva de magnetización del material del núcleo se puede ver en la figura 2. Suponga un incremento de 5% del área efectiva en el entrehierro debido al efecto marginal. ¿Cuánta corriente se requiere para producir en el entrehierro una densidad de flujo de 0.5 (T)? ¿Cuáles son las densidades de flujo en los cuatro lados del núcleo para esa corriente en la bobina? ¿Cuál es el flujo total presente en el entrehierro?

Figura 1. Núcleo con dos columnas y entrehierro.

Solución.

El área efectiva es

$A_{eff} = (0.05 \ m)(0.05 \ m)(1.05)$

$A_{eff} = 0.0026 \ m^2$

El flujo total es

$\phi = B \ E_{eff}$

$\phi = (0.5 \ T)(0.0026 \ m^2)$

$\phi = 0.0013 \ Wb$

El resultado de este flujo pertenece al 0.5 T de la densidad de flujo correspondiente al entrehierro y al flujo total del núcleo.

Este flujo requiere una densidad de flujo en la columna derecha de

$\phi = B_{der} \ A_{der}$

$\displaystyle B_{der} = \frac{\phi}{A_der}$

$\displaystyle B_{der} = \frac{0.0013 \ Wb}{(0.05 \ m)(0.05 \ m)}$

$B_{der} = 0.52 \ T$

La densidad de flujo en la parte izquierda del núcleo es

$\displaystyle B_{izq} = \frac{\phi}{A_{izq}}$

$\displaystyle B_{izq} = \frac{0.0013 \ Wb}{(0.10 \ m)(0.05 \ m)}$

$B_{izq} = 0.26 \ T$

La densidad de flujo en la parte superior del núcleo es

$\displaystyle B_{arriba} = \frac{\phi}{A_{arriba}}$

$\displaystyle B_{arriba} = \frac{0.0013 \ Wb}{(0.05 \ m)(0.10 \ m)}$

$B_{arriba} = 0.26 \ T$

La densidad de flujo en la parte inferior del núcleo es

$\displaystyle B_{abajo} = \frac{\phi}{A_{abajo}}$

$\displaystyle B_{abajo} = \frac{0.0013 \ Wb}{(0.05 \ m)(0.10 \ m)}$

$B_{abajo} = 0.26 \ T$

Analizando la curva de magnetización de la figura 2, tomando el valor de la densidad magnética, se puede determinar la intensidad magnética.

Figura 3. Ubicando el valor de la intensidad magnética para una densidad de flujo de 0.50 T por medio de la curva de magnetización.

La intensidad magnética para una densidad de flujo de 0.52 T es

$H = 410 \ (A \cdot espiras / m)$

Analizando la curva de magnetización de la figura 2, tomando el valor de la densidad magnética, se puede determinar la intensidad magnética.

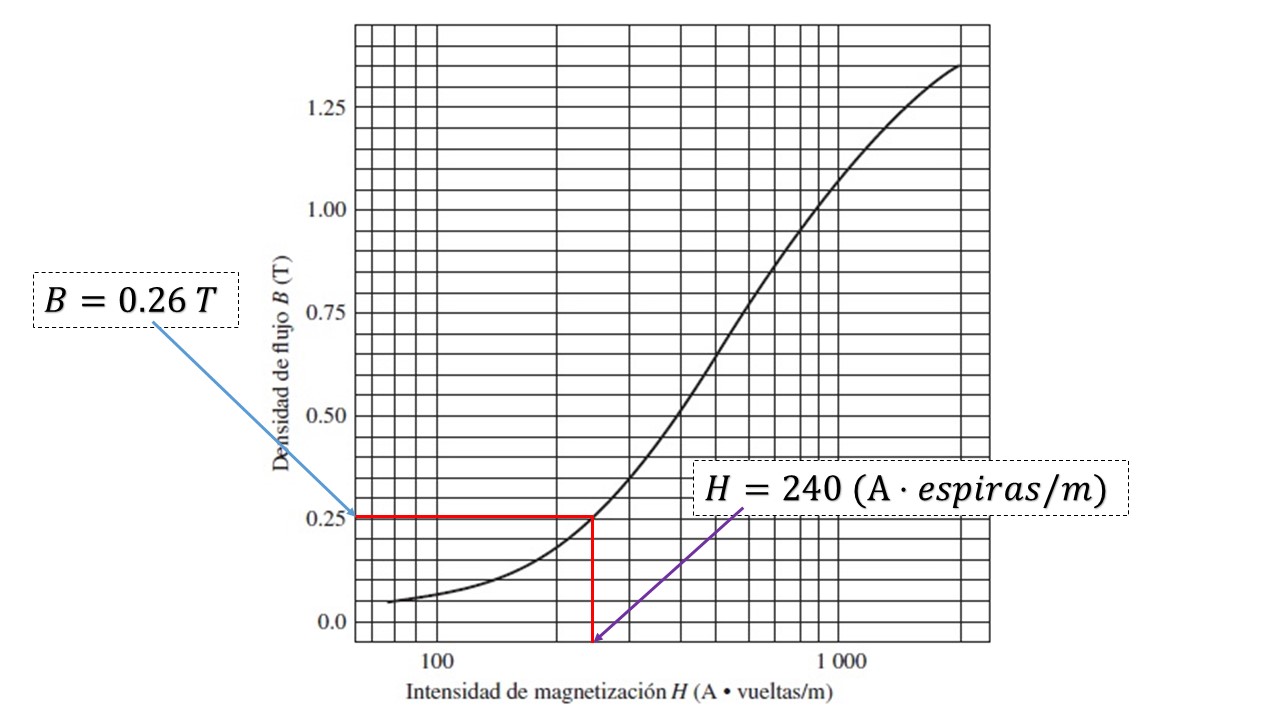
Figura 4. Ubicando el valor de la intensidad magnética para una densidad de flujo magnético de 0.26 T por medio de la curva de magnetización.

La intensidad magnética para una densidad de flujo de 0.52 T es

$H = 240 \ (A \cdot espiras / m)$

La intensidad magnética requerida para producir una densidad de flujo de 0.5 T en el entrehierro es de

$B_{entrehierro} = \mu_0 \ H_{entrehierro}$

$\displaystyle H_{entrehierro} = \frac{B_{entrehierro}}{\mu_0}$

$\displaystyle H_{entrehierro} = \frac{0.5 \ T}{4 \ pi \times 10^{-7}}$

$H_{entrehierro} = 397,886.43 \ (A \cdot espiras / m)$

La fuerza magnetomotriz es de

$\mathcal{F} = H_{entrehierro} \ l_{entrehierro} + H_{der} \ l_{der} + H_{izq} \ l_{izq} + H_{arriba} \ l_{arriba} + H_{abajo} \ l_{abajo}$

$\mathcal{F} = (397,886.43)(0.0005) + (410)(0.40) + (240)(0.40) + (240)(0.375) + (240)(0.375)$

$\mathcal{F} = 198.943 + 164 + 96 + 90 + 90$

$\mathcal{F} = 638.943 \ (A \cdot espiras)$

Finalmente, la corriente requerida es

$\mathcal{F} = N \ i$

$\displaystyle i = \frac{\mathcal{F}}{N}$

$\displaystyle i = \frac{638.943 \ (A \cdot espiras)}{1000 \ espiras}$

$\mathbf{ \therefore i \approx 0.639 \ A}$

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

9 comentarios sobre “Circuitos magnéticos. Problema 7. Máquinas eléctricas.”

yaneth dice:

5 octubre, 2020 a las 8:47 pm

de donde saca el area efectiva?

Me gustaMe gusta

Responder
1. Cesar Augusto dice:
  
  10 octubre, 2020 a las 2:02 pm
  
  Se calcula multiplicando el área de la sección transversal del entrehierro por el porcentaje del efecto marginal; como habla de un incremento sería sumar el 100% más el 5% del incremento (es decir 105% o artiméticamente, 1.05). El área efectiva está denominado como A_(eff). Saludos Yaneth.
  
  Me gustaMe gusta
  
  Responder
alex dice:

20 noviembre, 2020 a las 9:31 am

como hallas exactamente la intensidad magnetica, solo analizas la grafica o usas una formula para hallar el valor correcto y exacto

Me gustaMe gusta

Responder
1. Cesar Augusto dice:
  
  20 noviembre, 2020 a las 7:21 pm
  
  Hola alex. Para obtener la intensidad magnética solo basta con utilizar la tabla y considerar un valor muy aproximado (ya que puede variar).
  
  Me gustaMe gusta
  
  Responder
Bryam Duque dice:

16 diciembre, 2020 a las 4:24 pm

Muy buenas tardes! Muchas gracias por la explicación del ejercicio.
Me gustaría hacer una pregunta. ¿Por que, al final del ejercicio, tomas una longitud de arriba y de abajo de 0,24 m? ¿No debería ser 5cm + 30 cm + 2,5cm = 37,5cm o 0,375 m?
Quedo atento, muchas gracias!

Me gustaMe gusta

Responder
1. Bryam dice:
  
  16 diciembre, 2020 a las 4:28 pm
  
  Mmmm vi que el 0,24 es por la H, pero entonces jejeje disculpa, ahi viene entonces otra pregunta, ¿ Por que tomas 0,24 y 0,4, no debería ser 240 y 410?
  
  Me gustaMe gusta
  
  Responder
  1. Cesar Augusto dice:
    
    16 diciembre, 2020 a las 6:38 pm
    
    Buenas tardes. Disculpa la molestia con estos detalles. Ya se corrigió y se tienen los resultados actualizados. Saludos.
    
    Me gustaMe gusta
Marcos dice:

17 septiembre, 2021 a las 2:03 am

Por que pones en la longitud izquierda .375, no debería ser .40 tambien como en el caso de la derecha?

Me gustaMe gusta

Responder
1. Cesar Reyes dice:
  
  18 septiembre, 2021 a las 7:24 pm
  
  Hola Marcos. Gracias por visitarme y también por la observación que hiciste. Ya se realizó la corrección y está actualizado. Saludos…
  
  Me gustaMe gusta
  
  Responder