Circuitos magnéticos. Problema 10. Máquinas eléctricas.

Problema.

El núcleo que se muestra en la figura 1.1.30 tiene el flujo $\phi$ que se puede apreciar en la figura 1.1.31. Dibuje el voltaje de las terminales de la bobina.

Figura 1.1.30 Núcleo ferromagnético.

Figura 1.1.31 Representación gráfica de diferentes cantidades de flujo.

Solución.

Por ley de Lorentz, un incremento de flujo en la dirección mostrada en el núcleo producirá un voltaje que tiende a oponerse ese incremento. Este voltaje va a tenerla misma polaridad con la dirección mostrada del núcleo (figura 1.1.30). El voltaje inducido en el núcleo se obtiene mediante la siguiente ecuación

$\displaystyle e_{ind} = N \cdot \frac{d\phi}{dt}$

Para obtener lo deseado, se analiza la figura 1.1.31 utilizando el método de punto-pendiente.

En el intervalo $0 < t < 2$ , los puntos a tomar son $(0,0)$ y $(2,0.010)$ . La ecuación de flujo es

$\displaystyle \phi - \phi_1 = \left(\frac{\phi_2 - \phi_1}{t_2 - t_1} \right)(t-t_1)$

$\displaystyle \phi - 0 = \left(\frac{0.010 - 0}{2 - 0}\right)(t-0)$

$\phi = 0.005t \ (Wb)$

El voltaje inducido para este intervalo es

$\displaystyle e_{ind} = N \cdot \frac{d\phi}{dt}$

$\displaystyle e_{ind} = (500) \cdot \frac{d}{dt}(0.005t)$

$\displaystyle e_{ind} = (500 \ vueltas) (0.005 \ Wb)$

$\displaystyle e_{ind} = 2.5 \ (V)$

En el intervalo $2 < t < 5$ , los puntos a tomar son $(2,0.010)$ y $(5,-0.010)$ . La ecuación de flujo es

$\displaystyle \phi - \phi_1 = \left(\frac{\phi_2 - \phi_1}{t_2 - t_1} \right)(t-t_1)$

$\displaystyle \phi - 0.010 = \left(\frac{-0.010 - 0.010}{5 - 2} \right)(t-2)$

$\phi = -0.003 - 0.0067t \ (Wb)$

El voltaje inducido para este intervalo es

$\displaystyle e_{ind} = N \cdot \frac{d\phi}{dt}$

$\displaystyle e_{ind} = (500) \cdot \frac{d}{dt}(-0.003 - 0.0067t)$

$\displaystyle e_{ind} = (500) (- 0.0067)$

$\displaystyle e_{ind} = - 3.35 \ (V)$

En el intervalo $5 < t < 7$ , los puntos a tomar son $(5,-0.010)$ y $(7,0)$ . La ecuación de flujo es

$\displaystyle \phi - \phi_1 = \left(\frac{\phi_2 - \phi_1}{t_2 - t_1} \right)(t-t_1)$

$\displaystyle \phi - (-0.010) = \left[\frac{0 - (-0.010)}{7 - 5} \right](t-5)$

$\phi = -0.035 + 0.005t \ (Wb)$

El voltaje inducido para este intervalo es

$\displaystyle e_{ind} = N \cdot \frac{d\phi}{dt}$

$\displaystyle e_{ind} = (500) \cdot \frac{d}{dt}(-0.035 + 0.005t)$

$\displaystyle e_{ind} = (500) (0.005)$

$\displaystyle e_{ind} = 2.5 \ (V)$

En el intervalo $7 < t < 8$ , los puntos a tomar son $(7,0)$ y $(8,0.010)$ . La ecuación de flujo es

$\displaystyle \phi - \phi_1 = \left(\frac{\phi_2 - \phi_1}{t_2 - t_1} \right)(t-t_1)$

$\displaystyle \phi - 0 = \left(\frac{0.010 - 0}{8 - 7} \right)(t-7)$

$\phi = - 0.070 + 0.010t \ (Wb)$

El voltaje inducido para este intervalo es

$\displaystyle e_{ind} = N \cdot \frac{d\phi}{dt}$

$\displaystyle e_{ind} = (500) \cdot \frac{d}{dt}(- 0.070 + 0.010t)$

$\displaystyle e_{ind} = (500) (0.010t)$

$\displaystyle e_{ind} = 5 \ (V)$

En la siguiente tabla se muestra un resumen de los valores calculados.

Intervalo (s)	Voltaje inducido (V)
0 < t < 2	2.5
2 < t < 5	-3.35
5 < t < 7	2. 5
7 < t < 8	5

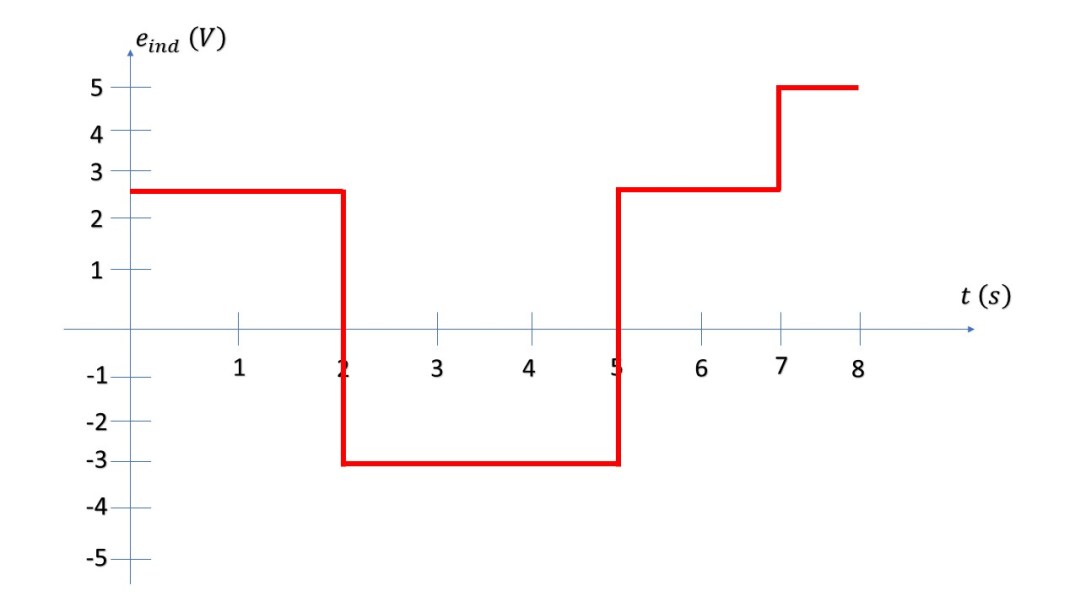
Tomando estos datos, se tiene el siguiente resultado esperado (figura 1.1.33).

figura 1.1.32 — Figura 1.1.33 Representación gráfica del voltaje inducido resultante.

Circuitos magnéticos. Problema 10. Máquinas eléctricas.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Circuitos magnéticos. Problema 10. Máquinas eléctricas.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta