Ecuaciones diferenciales exactas. Ecuaciones diferenciales.

La condición necesaria y suficiente de

$M(x,y) dx + N(x,y) dy = 0$ – – – – – (1)

para ser exacta es

$\displaystyle \frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}$ – – – – (2)

A veces se ve que una ecuación es exacta después de una agrupación adecuada de sus términos. La ecuación así ordenada se puede integrar término a término.

Caso 1. Cuando la ecuación diferencial es exacta. Si (1) es la diferencial exacta de la ecuación $\mu (x,y) = C$ ,

$\displaystyle d\mu = \frac{\partial \mu}{\partial x} dx + \frac{\partial \mu}{\partial y} dy = M(x,y) dx + N(x,y) dy$

Entonces

$\displaystyle \frac{\partial \mu}{\partial x} dx = M(x,y)$ y $\displaystyle \mu (x,y) = \int{M(x,y) dx} + \phi (y)$

Después,

$\displaystyle \frac{\partial \mu}{\partial y} = \frac{\partial}{\partial y} \left[\int{M(x,y) \ dx} \right] + \frac{\partial \phi}{\partial y} = N(x,y)$

De donde $\displaystyle \frac{d \phi}{dy} = \phi'(y)$ y, por tanto, se puede hallar $\phi (y)$ .

Caso 2. Cuando la ecuación diferencial no es exacta. Si la (1) no es exacta se buscará un factor integrante.

a) Si

$\displaystyle \frac{\frac{\partial M}{\partial y} - \frac{\partial N}{\partial x}}{N} = f(x)$ , función solo de «x», entonces $\displaystyle e^{\int{f(x) dx}}$ es el factor integrante de (1).

$\displaystyle \frac{\frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}}{M} = g(y)$ , función sólo de «y», entonces $\displaystyle e^{\int{g(y) dy}}$ es un factor integrante de (1).

b) Si (1) es homogénea y $Mx + Ny \ne 0$ , entonces $\displaystyle \frac{1}{Mx + Ny}$ es un factor integrante.

c) Si (1) se puede escribir de la forma $yF(xy) dx + xg(xy) dy = 0$ , donde $f(xy) \ne g(xy)$ , entonces

$\displaystyle \frac{1}{xy[f(xy)-g(xy)]} = \frac{1}{Mx-Ny}$

es un factor integrante.

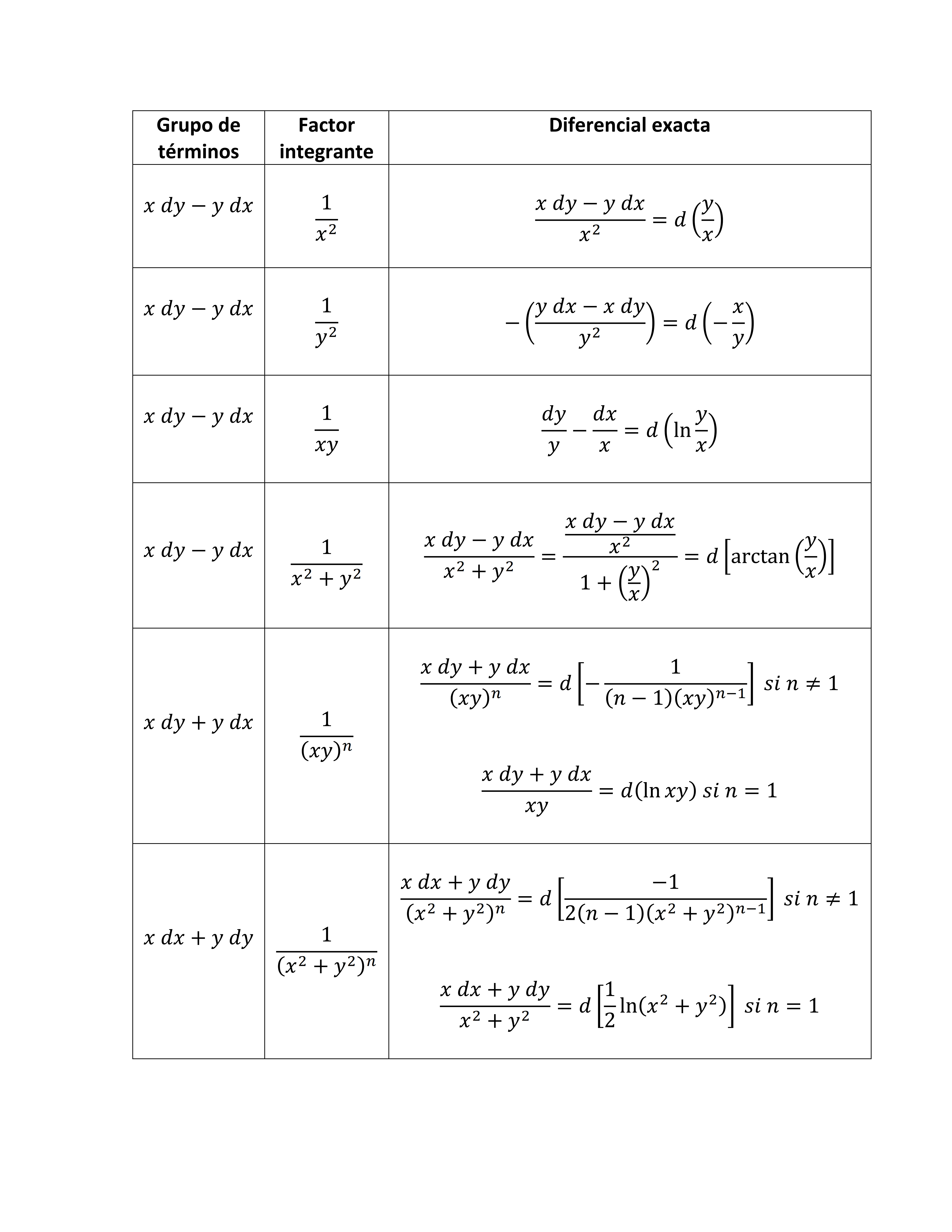
d) A veces se halla un factor integrante por inspección, después de agrupar los términos de la ecuación, al reconocer un cierto grupo de términos que van formando parte de una diferencial exacta.

Grupo de términos_factor integrante y diferencial exacta_001 — Tabla 1. Grupo de términos con su respectivo factor integrante y su diferencial exacta equivalente.

e) La ecuación $x^r y^s (my dx + nx dy) + x^p y^\sigma (\mu y dx + v x dy) = 0$ , donde r, s, m, n, p, σ, μ y v son constantes y $m v - n \mu \ne 0$ tiene un factor integrante de la forma $x^\alpha y^\beta$ . El método de resolución que da normalmente consiste en determinar α y β mediante ciertas fórmulas deducidas.

Problemas resueltos del caso 1

Problema 1. Resolver $(2x^3 + 3y) \ dx + (3x+y-1) \ dy = 0$

Solución. Primero se identifica las funciones $M$ y $N$

$M(x,y) = M = 2x^3 + 3y$ y $N(x,y) = N = 3x+y-1$

Después, se verifica si las ecuación es exacta.

$\displaystyle \frac{\partial}{\partial y} M(x,y) = \frac{\partial}{\partial y}(2x^3+3y) = 3$

$\displaystyle \frac{\partial}{\partial x} N(x,y) = \frac{\partial}{\partial x} (3x+y-1) = 3$

Observando que $\displaystyle \frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}$ , significa que la ecuación diferencial es exacta.

Ahora, determinando $\mu (x,y)$

$\displaystyle \mu (x,y) = \int{M(x,y) \ dx} = \int{(2x^3+3y) \ dx}$

$\displaystyle \mu (x,y) = \frac{1}{2} x^4 + 3xy + \phi(y)$

Para conocer el equivalente de $\phi (y)$ , se deriva $\mu (x,y)$ parcialmente con respecto a $y$ .

$\displaystyle \frac{\partial \mu}{\partial y} = \frac{\partial}{\partial y} \left[\frac{1}{2} x^4 + 3xy + \phi(y) \right]$

$\displaystyle \frac{\partial \mu}{\partial y} = 3x + \frac{\partial \phi}{\partial y}$

Recordando que $\displaystyle N(x,y) = \frac{\partial \mu}{\partial y}$ , resulta lo siguiente

$\displaystyle N(x,y) = 3x + \frac{\partial \phi}{\partial y}$

$\displaystyle 3x+y-1 = 3x + \frac{\partial \phi}{\partial y}$

$\displaystyle \frac{\partial \phi}{\partial y} = y - 1$

$\displaystyle d\phi = (y-1) \ dy$

$\displaystyle \int{d\phi} = \int{(y-1) \ dy}$

$\displaystyle \phi(x,y) = \frac{1}{2}y^2 - y$

Regresando a la expresión de $\mu$ y sustituyendo

$\displaystyle \mu (x,y) = \frac{1}{2}x^4 + 3xy + \phi(y)$

$\displaystyle \mu (x,y) = \frac{1}{2} x^4 + 3xy + \frac{1}{2} y^2 - y$

Recordando que $\mu (x,y) = C$ , la primitiva (el resultado final) es

$\displaystyle \therefore \frac{1}{2} x^4 + 3xy + \frac{1}{2} y^2 - y = C$

Problema 2. Resolver $(y^2 e^{xy^2} + 4x^3) \ dx + (2xye^{xy^2} - 3y^2) \ dy = 0$ .

Solución. Primero se identifican las funciones $M(x,y) = M$ y $N(x,y)=N$ .

$M(x,y) = y^2e^{xy^2} + 4x^3$ y $N(x,y) = 2xye^{xy^2} - 3y^2$

Derivando $M(x,y)$ parcialmente con respecto a $y$

$\displaystyle \frac{\partial M}{\partial y} = \frac{\partial}{\partial y} [y^2 e^{xy^2} + 4x^3] = 2ye^{xy^2} + 2xy^3 e^{xy^2}$

Y derivando $N(x,y)$ parcialmente con respecto a $x$

$\displaystyle \frac{\partial N}{\partial x} = \frac{\partial}{\partial x}[2xye^{xy^2} - 3y^2] = 2ye^{xy^2} + 2xy^3 e^{xy^2}$

Se observa que $\displaystyle \frac{\partial M}{\partial y} = \frac{\partial N}{\partial y}$ , lo cual, significa que la ecuación diferencial es exacta.

Ahora, determinando $\mu (x,y)$

$\displaystyle \mu (x,y) = \int{(y^2 e^{xy^2} + 4x^3) \ dx}$

$\displaystyle \mu (x,y) = e^{xy^2} + x^4 + \phi(y)$

Después, derivando $\mu (x,y)$ parcialmente con respecto a $y$ , resulta lo siguiente

$\displaystyle \frac{\partial \mu}{\partial y} = \frac{\partial}{\partial y} [e^{xy^2} + x^4 + \phi(y)]$

$\displaystyle \frac{\partial \mu}{\partial y} = 2xy e^{xy^2} + \frac{\partial \phi}{\partial y}$

Recordando que $\displaystyle \frac{\partial \mu}{\partial y} = N(x,y)$ , se obtiene el equivalente de $\phi (y)$ .

$\displaystyle N(x,y) = 2xy e^{xy^2} + \frac{\partial \phi}{\partial y}$

$\displaystyle 2xye^{xy^2} - 3y^2 = 2xy e^{xy^2} + \frac{\partial \phi}{\partial y}$

$\displaystyle \frac{\partial \phi}{\partial y} = -3y^2$

$\displaystyle d \phi = -3y^2 \ dy$

$\displaystyle \int{d \phi} = - \int{3y^2 \ dy}$

$\displaystyle \phi (y) = - y^3$

Regresando a la expresión de $\mu (x,y)$ y sustituyendo

$\displaystyle \mu (x,y) = e^{xy^2} + x^4 + \phi(y)$

$\displaystyle \mu (x,y) = e^{xy^2} + x^4 - y^3$

Recordando que $\mu (x,y) = C$ , la primitiva (resultado final) es

$\displaystyle \therefore e^{xy^2} + x^4 - y^3$

Problemas resueltos del caso 2

Problema 1. Resolver $(x^2+y^2+x) \ dx + xy \ dy = 0$ .

Solución. Se identifican las funciones $M(x,y)$ y $N(x,y)$ .

$M(x,y) = x^2+y^2+x$ y $N(x,y) = xy$

Derivando $M(x,y)$ parcialmente con respecto a $y$

$\displaystyle \frac{\partial M}{\partial y} = \frac{\partial}{\partial y} [x^2+y^2+x] = 2y$

Y derivando $N(x,y)$ parcialmente con respecto a $x$

$\displaystyle \frac{\partial N}{\partial x} = \frac{\partial}{\partial x} [xy] = y$

Se observa que $\displaystyle \frac{\partial M}{\partial y} \ne \frac{\partial N}{\partial x}$ , lo cual, significa que la ecuación diferencial no es exacta. Para transformar esta ecuación diferencial en exacta, es necesario hallar el factor integrante. Utilizando la fórmula

$\displaystyle f(x) = \frac{\frac{\partial M}{\partial y} - \frac{\partial N}{\partial x}}{N} = \frac{2y - y}{xy} = \frac{y}{xy} = \frac{1}{x}$

Después

$\displaystyle e^{\int{f(x) \ dx}} = e^{\int{\frac{1}{x} \ dx}} = e^{\ln{x}} = x$

que esto representa el factor integrante. Multiplicándolo por toda la ecuación diferencial del problema, se tiene una nueva epxresión.

$\displaystyle x [(x^2+y^2+x) \ dx + xy \ dy = 0]$

$\displaystyle (x^3+xy^2+x^2) \ dx + x^2y \ dy = 0$

Localizando las nuevas funciones $M(x,y)$ y $N(x,y)$

$M(x,y) = x^3+xy^2+x^2$ y $N(x,y) = x^2y$

Nuevamente se derivan ambas funciones

$\displaystyle \frac{\partial M}{\partial y} = 2xy$

$\displaystyle \frac{\partial N}{\partial x} = 2xy$

Y esta ecuación diferencial ya es exacta.

Ahora, determinando $\mu (x,y)$

$\displaystyle \mu (x,y) = \int{(x^3+xy^2+x^2) \ dx}$

$\displaystyle \mu (x,y) = \frac{1}{4} x^4 + \frac{1}{2} x^2 y^2 + \frac{1}{3} x^3 + \phi (y)$

Para encontrar el equivalente de $\phi (y)$ , se deriva $\mu (x,y)$ con respecto a $y$ . Posteriormente, se despejan las diferencial y por último se integra

$\displaystyle \frac{\partial \mu}{\partial y} = \frac{\partial}{\partial y} \left[\frac{1}{4} x^4 + \frac{1}{2}x^2 y^2 + \frac{1}{3} x^3 + \phi(y) \right]$

$\displaystyle \frac{\partial \mu}{\partial y} = x^2 y + \frac{\partial \phi}{\partial y}$

Recordando que $\displaystyle \frac{\partial \mu}{\partial y} = N(x,y)$ , se obtiene lo siguiente

$\displaystyle N(x,y) = x^2 y + \frac{\partial \phi}{\partial y}$

$\displaystyle x^2 y = x^2 y + \frac{\partial \phi}{\partial y}$

$\displaystyle \frac{\partial \phi}{\partial y} = 0$

$d \phi = 0 \ dy$

$\displaystyle \int{d \phi} = \int{0 \ dy}$

$\phi (y) = K$

Regresando al resultado de $\mu (x,y)$ y sustituyendo

$\displaystyle \mu (x,y) = \frac{1}{4} x^4 + \frac{1}{2} x^2 y^2 + \frac{1}{3} x^3 + \phi(y)$

$\displaystyle \mu (x,y) = \frac{1}{4} x^4 + \frac{1}{2} x^2 y^2 + \frac{1}{3} x^3 + K$

Por ultimo, $\mu (x,y) = C$ , por lo tanto

$\displaystyle \frac{1}{4} x^4 + \frac{1}{2} x^2 y^2 + \frac{1}{3} x^3 + K =C$

$\displaystyle \frac{1}{4} x^4 + \frac{1}{2} x^2 y^2 + \frac{1}{3} x^3 = C-K$

$\displaystyle \therefore \frac{1}{4} x^4 + \frac{1}{2} x^2 y^2 + \frac{1}{3} x^3 = C$

Problema 2. Resolver $(2x^4 e^y + 2xy^3 + y)\ dx + (x^2 y^4 e^y - x^2 y^2 - 3x) \ dy =0$ .

Solución. Identificando las funciones $M(x,y)$ y $N(x,y)$

$M(x,y) = 2x^4 e^y + 2xy^3 + y$ y $N(x,y) = x^2 y^4 e^y - x^2$

Se derivan parcialmente con respecto a $x$ y a $y$

$\displaystyle \frac{\partial M}{\partial y} = 2x^4 e^y + 6xy^2 + 1$

$\displaystyle \frac{\partial N}{\partial x} = 2xy^4 e^y - 2x$

Se observa que $\displaystyle \frac{\partial M}{\partial y} \ne \frac{\partial N}{\partial x}$ , lo cual, significa que la ecuación diferencial no es exacta.

Para que la ecuación sea exacta, primero se determina el factor integrante

$\displaystyle g(y) = -\frac{\frac{\partial M}{\partial y} - \frac{\partial N}{\partial x}}{M}$

$\displaystyle g(y) = -\frac{(8xy^3 e^y + 2xy^4 e^y + 6xy^2 +1)-(2xy^4 e^y - 2xy^2 - 3)}{2xy^4 e^y + 2xy^3 + y} = \frac{8xy^3 e^y + 2xy^4 e^y + 6xy^2 +1 - 2xy^4 e^y + 2xy^2 + 3}{2xy^4 e^y + 2xy^3 + y}$

$\displaystyle g(y) = - \frac{8xy^3 e^y + 8xy^2 + 4}{2xy^4 e^y + 2xy^3 + y} = -\frac{4(2xy^3 e^y + 2xy^2 + 1}{y(2xy^3 e^y + 2xy^2 + 1)} = - \frac{4}{y}$

Luego

$\displaystyle e^{\int{(-\frac{4}{y}) \ dy}} = e^{-4 \ln{y}} = e^{\ln{y^{-4}}} = y^{-4} = \frac{1}{y^4}$

Multiplicando el factor integrante por toda la ecuación diferencial del problema

$\displaystyle \frac{1}{y^4} \left[(2xy^4 e^y + 2xy^3 + y) \ dx + (x^2 y^4 e^y - x^2 y^2 - 3x) \ dy = 0 \right]$

$\displaystyle \frac{2xy^4 e^y + 2xy^3 + y}{y^4} \ dx + \frac{x^2 y^4 e^y - x^2 y^2 - 3x}{y^4} \ dy = 0$

$\displaystyle \left(2x e^y + \frac{2x}{y} + \frac{1}{y^3} \right) \ dx + \left(x^2 e^y - \frac{x^2}{y^2} - \frac{3x}{y^4} \right) \ dy = 0$

Identificando nuevamente las funciones $M(x,y) = M$ y $N(x,y)=N$

$\displaystyle M(x,y) = 2xe^y + \frac{2x}{y} + \frac{1}{y^3}$ y $\displaystyle N(x,y) = x^2 e^y - \frac{x^2}{y^2} - \frac{3x}{y^4}$

Y también se vuelven a determinar sus derivadas parciales

$\displaystyle \frac{\partial M}{\partial y} = 2xe^y - \frac{2x}{y^2} - \frac{3}{y^4}$

$\displaystyle \frac{\partial N}{\partial x} = 2xe^y - \frac{2x}{y^2} - \frac{3}{y^4}$

Y en esta ocasión, como $\displaystyle \frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}$ , significa que esta nueva ecuación diferencial ya es exacta. Continuando con el procedimiento para determinar la primitiva

$\displaystyle \mu (x,y) = \int{M(x,y) \ dx} = \int{\left(2xe^y + \frac{2x}{y} + \frac{1}{y^3} \right) \ dx}$

$\displaystyle \mu (x,y) = x^2 e^y + \frac{x^2}{y} + \frac{x}{y^3} + \phi (y)$

Derivando parcialmente con respecto a $y$

$\displaystyle \frac{\partial \mu}{\partial y} = \frac{\partial}{\partial y} \left[x^2 e^y + \frac{x^2}{y} + \frac{x}{y^3} + \frac{\partial \phi}{\partial y} \right]$

$\displaystyle \frac{\partial \mu}{\partial y} = x^2 e^y - \frac{x^2}{y^2} - \frac{3x}{y^4} + \frac{\partial \phi}{\partial y}$

Recordando que $\displaystyle \frac{\partial \mu}{\partial y} = N(x,y)$ , resulta que

$\displaystyle x^2 e^y - \frac{x^2}{y^2} - \frac{3x}{y^4} = x^2 e^y - \frac{x^2}{y^2} - \frac{3x}{y^2} + \frac{\partial \phi}{\partial y}$

$\displaystyle \frac{\partial \phi}{\partial y} = 0$

$d\phi = 0 \cdot dy$

$\displaystyle \int{d \phi} = \int{0 \ dy}$

$\phi (y) = K$

Regresando a la expresión de $\mu (x,y)$ y sustituyendo

$\displaystyle \mu (x,y) = x^2 e^y + \frac{x^2}{y} + \frac{x}{y^3} + \phi (y)$

$\displaystyle \mu (x,y) = x^2 e^y + \frac{x^2}{y} + \frac{x}{y^3} + K$

Recordando que $\mu (x,y) = C$ , el resultado final es

$\displaystyle x^2 e^y + \frac{x^2}{y} + \frac{x}{y^3} + K = C$

$\displaystyle x^2 e^y + \frac{x^2}{y} + \frac{x}{y^3} = C - K$

$\displaystyle \therefore x^2 e^y + \frac{x^2}{y} + \frac{x}{y^3} = C$

Problema 3. Resolver $(x^4 + y^4) \ dx - xy^3 \ dy = 0$ .

Solución. Identificando las funciones $M(x,y) = M$ y $N(x,y) = N$

$M(x,y) = x^4 + y^4$ y $N(x,y) = - xy^3$

Y derivándolas parcialmente

$\displaystyle \frac{\partial M}{\partial y} = 4y^3$ y $\displaystyle \frac{\partial N}{\partial x} = - y^3$

Se observa que $\displaystyle \frac{\partial M}{\partial y} \ne \frac{\partial N}{\partial x}$ , lo cual significa que la ecuación diferencial no es exacta.

Por inspección, se tiene una ecuación diferencial homogénea de cuarto grado. Para este caso, se tiene una fórmula para determinar el factor integral

$\displaystyle \frac{1}{Mx + Ny} = \frac{1}{(x^4 + y^4)x + (-xy^3)y} = \frac{1}{x^5 + xy^4 - xy^4} = \frac{1}{x^5}$

Multiplicándolo por toda la ecuación diferencial

$\displaystyle \frac{1}{x^5} \left[(x^4+y^4) dx - xy^3 dy = 0 \right]$

$\displaystyle \left(\frac{1}{x} + \frac{y^4}{x^5} \right) \ dx - \frac{y^3}{x^4} \ dy = 0$

Identificando nuevamente las funciones $\displaystyle M(x,y) = M = \frac{1}{x} + \frac{y^4}{x^5}$ y $\displaystyle N(x,y) = N = - \frac{y^3}{x^4}$ . Derivando nuevamente

$\displaystyle \frac{\partial M}{\partial y} = \frac{4y^3}{x^5}$ y $\displaystyle \frac{\partial N}{\partial x} = \frac{4y^3}{x^5}$

Se observa que $\displaystyle \frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}$ , lo que significa que la nueva ecuación diferencial ya es exacta.

Continuando

$\displaystyle \mu (x,y) = \int{M(x,y) \ dx}= \int{\left(\frac{1}{x} + \frac{y^4}{x^5} \right) \ dx}$

$\displaystyle \mu (x,y) = \ln{x} - \frac{y^4}{4x^4} + \phi (y)$

Derivando parcialmente con respecto a $y$

$\displaystyle \frac{\partial \mu}{\partial y} = - \frac{y^3}{x^4} + \frac{\partial \phi}{\partial y}$

Recordando que $\displaystyle \frac{\partial \mu}{\partial y} = N(x,y)$ , resulta que

$\displaystyle - \frac{y^3}{x^4} = - \frac{y^3}{x^4} + \frac{\partial \phi}{\partial y}$

$\displaystyle \frac{\partial \phi}{\partial y} = 0$

$\displaystyle d \phi = 0 \cdot dy$

$\displaystyle \int{d \phi} = \int{0 \ dy}$

$\phi(y) = K$

Regresando a la expresión de $\mu (x,y)$ y sustituyendo

$\displaystyle \mu (x,y) = \ln{x} - \frac{y^4}{4 x^4} + K$

Recordando que $\mu (x,y) = C$ , la primitiva es

$\displaystyle \ln{x} - \frac{y^4}{4x^4} + K =C$

$\displaystyle \ln{x} - \frac{y^4}{4x^4} = C$

$\therefore 4x^4 \ln{x} - y^4 = Cx^4$

Problema 4. Resolver $y(x^2 y^2 + 2) \ dx + x(2 - 2x^2 y^2) \ dy = 0$ .

Solución. Se observa que las funciones son $M(x,y) = M = x^2 y^3 + 2y$ y $N(x,y) = N = 2x - 2x^3 y^2$ .

Al estudiar esta ecuación diferencial, se tiene que no es exacta. Esta ecuación tiene la forma $y \ f_1 (xy) \ dx + x f_2 (xy) \ dy = 0$ , por lo que se aplicará un procedimiento diferente para que la ecuación diferencial sea exacta. Utilizando la siguiente fórmula para calcular el factor integrante

$\displaystyle \frac{1}{Mx-Ny} = \frac{1}{(x^2 y^3 + 2y)x - (2x - 2x^3 y^2)y}$

$\displaystyle = \frac{1}{x^3 y^3 + 2xy - 2xy + 2x^3 y^3} = \frac{1}{3x^3 y^3}$

Multiplicando este factor integrante por toda la ecuación diferencial del problema

$\displaystyle \frac{1}{3x^3 y^3} \left[y(x^2 y^2 + 2) \ dx + x(2 - 2x^2 y^2) \ dy = 0 \right]$

$\displaystyle \left(\frac{x^2 y^2 + 2}{3x^3 y^2} \right) dx + \left( \frac{2 - 2x^2 y^2}{3x^2 y^3} \right) dy = 0$

$\displaystyle \left(\frac{1}{3x} + \frac{2}{3x^3 y^2} \right) dx + \left( \frac{2}{3x^2 y^3} - \frac{2}{3y} \right) dy = 0$

Con esta nueva ecuación diferencial, las nuevas funciones de $M(x,y)$ y $N(x,y)$ son $\displaystyle \frac{1}{3x} + \frac{2}{3x^3 y^2}$ y $\displaystyle \frac{2}{3x^2 y^3} - \frac{2}{3y}$ , respectivamente. Al derivarlo parcialmente con respecto a $x$ y $y$ , la ecuación diferencial ya es exacta. Continuando

$\displaystyle \mu (x,y) = \int{M(x,y) \ dx} = \int{\left(\frac{1}{3x} + \frac{2}{3x^3 y^2} \right) dx}$

$\displaystyle \mu (x,y) = \frac{1}{3} \ln{x} - \frac{1}{3x^2 y^2} + \phi (y)$

Derivando parcialmente este resultado con respecto a $y$ , resulta lo siguiente

$\displaystyle \frac{\partial \mu}{\partial y} = \frac{2}{3x^2 y^3} + \frac{\partial \phi}{\partial y}$

Recordando que $\displaystyle \frac{\partial \mu}{\partial y} = N(x,y)$ , por igualación y despejando la derivada parcial de $\phi$ , se tiene que

$\displaystyle \frac{2}{3x^2 y^3} - \frac{2}{3y} = \frac{2}{3x^2 y^3} + \frac{\partial \phi}{\partial y}$

$\displaystyle \frac{\partial \phi}{\partial y} = - \frac{2}{3y}$

$\displaystyle d \phi = -\frac{2}{3y} dy$

$\displaystyle \int{d \phi} = - \int{\frac{2}{3y} \ dy}$

$\displaystyle \phi (y) = - \frac{2}{3} \ln{y}$

Regresando y sustituyendo

$\displaystyle \mu (x,y) = \frac{1}{3x} - \frac{1}{3x^2 y^2} + \phi (y)$

$\displaystyle \mu (x,y) = \frac{1}{3x} - \frac{1}{3x^2 y^2} - \frac{2}{3} \ln{y}$

Recordando que $\mu (x,y) = C$ , la primitiva es

$\displaystyle \therefore \frac{1}{3x} - \frac{1}{3x^2 y^2} - \frac{2}{3} \ln{y} = C$

Problema 5. Resolver $y \ dx + x(1-3x^2 y^2) \ dy = 0$ .

Solución. Esta ecuación diferencial no es exacta, para este caso, se utilizará otra técnica. Realizando un acomodo en toda la ecuación diferencial

$y\ dx + x \ dy - 3x^3 y^2 \ dy = 0$

$\displaystyle (y \ dx + x \ dy) - 3x^3 y^2 \ dy = 0$

Observando el primer término, sugiere un factor integrante

$\displaystyle \frac{1}{(xy)^n} = \frac{1}{(xy)^3} = \frac{1}{x^3 y^3}$

donde se ha asignado a $n=3$ . Multiplicando el factor integrante por toda la ecuación diferencial

$\displaystyle \frac{1}{x^3 y^3} [(y dx + x dy) - 3x^3 y^2 dy] = 0$

$\displaystyle \frac{y \ dx + x \ dy}{x^3 y^3} - \frac{3}{y} \ dy = 0$

Aplicando la diferencial exacta en el primer término

$\displaystyle d \left[- \frac{1}{(3-1) (xy)^{3-1}} \right] - \frac{3}{y} \ dy = 0$

$\displaystyle d \left[- \frac{1}{2 (xy)^{2}} \right] - \frac{3}{y} \ dy = 0$

Integrando

$\displaystyle \int{d \left[- \frac{1}{2(xy)^2} \right]} - \int{\frac{3}{y} \ dy} = \int{0 \ dx}$

$\displaystyle -\frac{1}{2(xy)^2} - 3 \ln{y} = C$

Finalmente

$\displaystyle \therefore - \frac{1}{2x^2 y^2} - \ln{y^3} = C$

Problema 6. Resolver $x(4y \ dx + 2x \ dy) + y^3 (3y \ dx + 5x \ dy) = 0$ .

Solución. Esta ecuación diferencial no es exacta. Aplicando una técnica más para encontrar su primitiva, el procedimiento es el siguiente. Multiplicando por $x^{\alpha} y^{\beta}$ por toda la ecuación del problema

$\displaystyle x^{\alpha} y^{\beta} [x(4y dx + 2x dy) + y^3 (3y dx + 5x dy) = 0]$

$\displaystyle x^{\alpha} y^{\beta} [(4xy dx + 2x^2 dy) + (3y^4 dx + 5xy^3 dy) = 0]$

$(4x^{\alpha + 1} y^{\beta + 1} dx + 2x^{\alpha + 2} y^{\beta} dy) + (3x^{\alpha} y^{\beta + 4} dx + 5x^{\alpha + 1} y^{\beta + 3} dy) = 0$

Cada uno de sus dos términos es una diferencial exacta. Analizando el primer término, se toman cada variable que tiene mayor potencia (expresión de mayor suma) y se determina la diferencial de cada uno.

$d(x^{\alpha + 2} y^{\beta + 1}) = (\alpha + 2)x^{\alpha + 1} y^{\beta +1} dx + (\beta + 1) x^{\alpha + 2} y^{\beta} dy$

El resultado del primer término es proporcional al resultado de la primera diferencial.

$\displaystyle \frac{\alpha + 2}{4} = \frac{\beta +1}{2}$

$\alpha - 2\beta = 0$

Se aplica el mismo procedimiento para el segundo término.

$d(x^{\alpha + 1} y^{\beta + 4}) = (\alpha + 1) x^{\alpha} y^{\beta + 4}dx + (\beta +4) x^{\alpha + 1} y^{\beta + 3}$

El resultado del segundo término es proporcional al resultado de esta segunda diferencial.

$\displaystyle \frac{\alpha + 1}{3} = \frac{\beta + 4}{5}$

$5\alpha - 3\beta = 7$

Tomando la primera ecuación con está última, se obtiene un sistema de ecuaciones simultáneas con dos incógnitas. Resolviendo este sistema, se tiene que $\alpha = 2$ y $\beta = 1$ . Sustituyendo estos valores en la ecuación en la ecuación multiplicada por el factor integrante

$(4x^{\alpha + 1} y^{\beta + 1} dx + 2x^{\alpha + 2} y^{\beta} dy) + (3x^{\alpha} y^{\beta + 4} dx + 5x^{\alpha + 1} y^{\beta + 3} dy) = 0$

$(4x^{2 + 1} y^{1 + 1} dx + 2x^{2 + 2} y^{1} dy) + (3x^{2} y^{1 + 4} dx + 5x^{2 + 1} y^{1 + 3} dy) = 0$

$(4x^3 y^2 dx + 2x^4 y dy) + (3x^2 y^5 dx + 5x^3 y^4 dy) = 0$

Cada término del primer término tiene su propia diferencial exacta, y es

$d(x^4 y^2) + d(x^3 y^5) = 0 \ dx$

Integrando en cada término

$\displaystyle \int{d(x^4 y^2)} + \int{d(x^3 y^5)} = \int{0 \ dx}$

$x^4 y^2 + x^3 y^5 = C$

Este último resultado es la primitiva esperada.

2 comentarios sobre “Ecuaciones diferenciales exactas. Ecuaciones diferenciales.”

Brayan Ortiz dice:

16 mayo, 2021 a las 11:30 am

Hola, me podrías ayudar con esta ecuación diferencial exacta
(xy^2-y^3)dx + (1-xy^2)dy = 0

Me gustaMe gusta

Responder
packo fabian dice:

20 junio, 2021 a las 9:55 am

x\left(x^2+y^2-4\right)dx-y\left(x^2+y^2+4\right)dy\:=0 ; solucion con la Exacta

Me gustaMe gusta

Responder

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.

Ecuaciones diferenciales exactas. Ecuaciones diferenciales.

Problemas resueltos del caso 1

Problemas resueltos del caso 2

Comparte esto:

Relacionado

Publicado por Cesar Reyes

2 comentarios sobre “Ecuaciones diferenciales exactas. Ecuaciones diferenciales.”

Deja un comentario Cancelar la respuesta