Transformadores. Problema 21. Máquinas eléctricas.

Problema. Un transformador monofásico de 10 (kVA) y 480/120 (V) se utiliza como autotransformador y une una línea de distribución de 600 (V) con una carga de 480 (V). Se obtienen los siguientes datos cuando se le realizan pruebas como un transformador convencional que se tomaron del lado primario (480 V) del transformador.

Prueba de circuito abierto (en el lado secundario)	Prueba de cortocircuito (en el lado primario)
$V_{CAb} = 120 \ (V)$	$V_{CC} = 10.0 \ (V)$
$I_{CAb} = 1.60 \ (A)$	$I_{CC} = 10.6 \ (A)$
$P_{CAb} = 38 \ (W)$	$P_{CC} = 25 \ (W)$

a) Encuentre el circuito equivalente por unidad del transformador cuando se conecta de manera convencional. ¿Cuál es la eficiencia del transformador en condiciones nominales y un factor de potencia unitario? ¿Cuál es la regulación de voltaje en estas condiciones?

b) Dibuje las conexiones del transformador cuando se utiliza como un autotransformador reductor de 600/480 (V).

c) ¿Cuál es el valor nominal en kilovoltamperes del transformador cuando se utiliza con la conexión de autotransformador?

d) Responda la pregunta del inciso a) para la conexión como autotransformador.

Solución a). Primero se cálculo de la impedancia de base (referido al lado primario)

$\displaystyle Z_{base,P} = \frac{(V_P)^2}{S}$

$\displaystyle Z_{base,P} = \frac{(480)^2}{10 \times 10^3}$

$\displaystyle Z_{base,P} = 23.04 \ (\Omega)$

De los datos del circuito abierto, se obtiene los elementos de la rama de excitación (referido al lado primario). Para ello se determina la magnitud de la admitancia de excitación

$\displaystyle |Y_{EX}| = \frac{I_{\phi, CAb}}{V_{\phi, CAb}} = \frac{I_{CAb}}{V_{CAb}}$

$\displaystyle |Y_{EX}| = \frac{1.60 \ (A)}{120 \ (V)}$

$\displaystyle |Y_{EX}| = 13.333 \times 10^{-3} \ (S)$

El ángulo de la admitancia es

$\displaystyle \theta = \cos^{-1}{\left(\frac{P_{CAb}}{I_{CAb} \ V_{CAb}} \right)}$

$\displaystyle \theta = \cos^{-1}{\left(\frac{38}{(120)(1.6)} \right)}$

$\displaystyle \theta = 78.58$ °

El fasor de la admitancia es

$\displaystyle Y_{EX} = |Y_{EX}| \angle (-\theta)$

$\displaystyle Y_{EX} = 13.333 \times 10^{-3} \angle (-78.58) \ (S) = 2.64 \times 10^{-3} - j13.069 \times 10^{-3} \ (S)$

Por tanto, la resistencia es

$\displaystyle G_C = \frac{1}{R_C} \rightarrow R_C = \frac{1}{G_C}$

$\displaystyle R_C = \frac{1}{2.64 \times 10^{-3}} = 378.788 \ (\Omega)$

Y la reactancia es

$\displaystyle B_M = \frac{1}{X_M} \rightarrow X_M = \frac{1}{B_M}$

$\displaystyle X_M = \frac{1}{13.069 \times 10^{-3}} = 76.517 \ (\Omega)$

Convirtiéndolos a por unidad, resulta que

$\displaystyle R_{C,pu} = \frac{R_C}{Z_{base,P}}$

$\displaystyle R_{C,pu} = \frac{378.788}{23.04}$

$\displaystyle R_{C,pu} = 16.44 \ (pu)$

$\displaystyle X_{M,pu} = \frac{X_M}{Z_{base,P}}$

$\displaystyle X_{M,pu} = \frac{76.517}{23.04}$

$\displaystyle X_{M,pu} = 3.321 \ (pu)$

De los datos del cortociruito, se obtiene los elementos de la impedancia. Para ello, se calcula primero la magnitud de la impedancia,

$\displaystyle |Z_{SE}| = \frac{V_{CC}}{I_{CC}}$

$\displaystyle |Z_{SE}| = \frac{10}{10.6}$

$\displaystyle |Z_{SE}| = 0.943 \ (\Omega)$

El ángulo de la impedancia es

$\displaystyle \theta = \cos^{-1}{\left(\frac{P_{CC}}{V_{CC} \cdot I_{CC}} \right)}$

$\displaystyle \theta = \cos^{-1}{\left(\frac{25}{(10) \cdot (10.6)} \right)}$

$\displaystyle \theta = 76.36$ °

el fasor de la impedancia es

$\displaystyle Z_{SE} = |Z_{SE}| \angle \theta \ (\Omega)$

$\displaystyle Z_{SE} = 0.943 \angle (76.43) \ (\Omega) = 0.222 + j0.916 \ (\Omega)$

Por tanto, la resistencia equivalente es

$\displaystyle R_{eq} = 0.222 \ (\Omega)$

y la reactancia equivalente es

$\displaystyle X_{eq} = 0.916 \ (\Omega)$

Convirtiéndolo a por unidad

$\displaystyle R_{eq,P} = \frac{R_{eq}}{Z_{base,P}}$

$\displaystyle R_{eq,P} = \frac{0.222}{23.04}$

$\displaystyle R_{eq,P} = 9.635 \times 10^{-3} \ (pu)$

$\displaystyle X_{eq,P} = \frac{X_{eq}}{Z_{base,P}}$

$\displaystyle X_{eq,P} = \frac{0.916}{23.04}$

$\displaystyle X_{eq,P} = 39.76\times 10^{-3} \ (pu)$

Por tanto, el circuito equivalente por unidad esperado es el siguiente

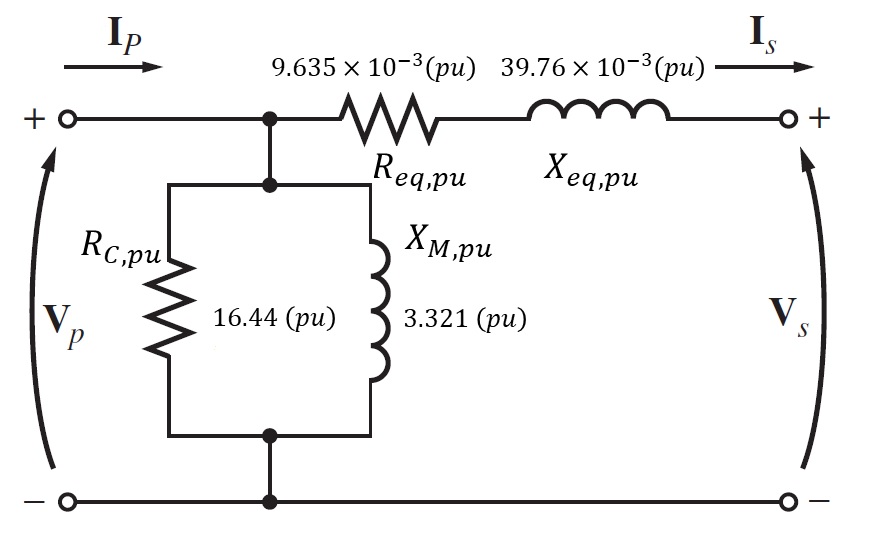
*Figura 2.21.1 Circuito equivalente por unidad.*

Por las condiciones nominales y un factor de potencia unitario, la potencia de entrada para este transformador sería $P_{ent} = 1 \ (pu)$ .

Ahora, calculando la potencia por pérdidas en el núcleo del transformador, se tiene que

$\displaystyle P_{nucleo} = \frac{V^2}{R_C}$

$\displaystyle P_{nucleo} = \frac{(1)^2}{16.44}$

$\displaystyle P_{nucleo} = 0.061 \ (pu)$

Después, calculando la potencia por pérdidas en el cobre del transformador, resulta

$P_{Cu} = R_{eq,pu} I^2$

$P_{Cu} = (9.635 \times 10^{-3})(1)^2$

$P_{Cu} = 9.635 \times 10^{-3} \ (pu) \approx 0.01 \ (pu)$

Y la potencia de salida es

$\displaystyle P_{sal} = V_S I_S \cos{\theta} = P_{ent} - P_{Cu} - P_{nucleo}$

$\displaystyle P_{sal} = 1 - 0.061 - 0.01$

$\displaystyle P_{sal} = 0.929 \ (pu)$

Finalmente, la eficiente del transformador es

$\displaystyle \eta = \frac{P_{sal}}{P_{ent}} \times 100$ %

$\displaystyle \eta = \frac{0.929}{1} \times 100$ %

$\displaystyle \therefore \eta = 92.9$ %

Por último de este inciso, antes de calcular la regulación de voltaje, primero se debe determinar el fasor de voltaje de salida sabiendo que el de entrada es $V_{ent} = 1 \angle 0$ . Entonces,

$\displaystyle \boldsymbol{V}_{sal} = \boldsymbol{V}_{ent} - R_{eq,pu} \boldsymbol{I} - jX_{eq,pu} \boldsymbol{I}$

$\displaystyle \boldsymbol{V}_{sal} = 1 \angle 0 - (9.635 \times 10^{-3})(1 \angle 0) - j39.76 \times 10^{-3}(1 \angle 0)$

$\displaystyle \boldsymbol{V}_{sal} = 1 \angle 0 - (9.635 \times 10^{-3} \angle 0)(1 \angle 0) - (39.76 \times 10^{-3} \angle 90)(1 \angle 0)$

$\displaystyle \boldsymbol{V}_{sal} = 1 \angle 0 - (9.635 \times 10^{-3} \angle 0) - (39.76 \times 10^{-3} \angle 90)$

$\displaystyle \boldsymbol{V}_{sal} = 1 + j0 - (9.635 \times 10^{-3} + j0) - (j39.76 \times 10^{-3})$

$\displaystyle \boldsymbol{V}_{sal} = 1 + j0 - 9.635 \times 10^{-3} - j0 - j39.76 \times 10^{-3} = 0.99 - j39.76\times 10^{-3} \ (pu)$

$\displaystyle \boldsymbol{V}_{sal} = 0.991 \angle (-2.13) \ (pu)$

Por tanto,

$\displaystyle RV = \frac{V_{ent} - V_{sal}}{V_{sal}} \times 100$ %

$\displaystyle RV = \frac{1 - 0.991}{0.991} \times 100$ %

$\displaystyle \therefore RV = 0.90$ %

Solución b). La conexión del autotransformador para 600/480 (V) es

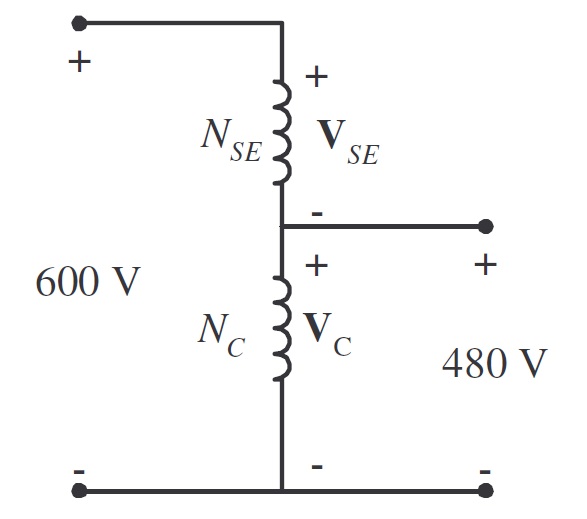
*Figura 2.21.2 Conexión adecuada del autotransformador reductor 600/480 (V).*

Solución c). Por medio de la figura 2.21.2, se sabe que

$\displaystyle \frac{V_C}{V_{SE}} = \frac{N_C}{N_{SE}}$

$\displaystyle \frac{480}{120} = \frac{N_C}{N_{SE}}$

$\displaystyle 4 = \frac{N_C}{N_{SE}}$

$\displaystyle 4 N_{SE} = N_C$

Así, el cálculo del valor nominal en kilovoltaperes se obtiene despejando $S_{ES}$ en base a la siguiente fórmula

$\displaystyle \frac{S_{ES}}{S_D} = \frac{N_C + N_{SE}}{N_{SE}}$

$\displaystyle S_{ES} = \left(\frac{N_C + N_{SE}}{N_{SE}} \right) S_D$

$\displaystyle S_{ES} = \left(\frac{4N_{SE} + N_{SE}}{N_{SE}} \right) (10 \times 10^3)$

$\displaystyle S_{ES} = (5) (10 \times 10^3)$

$\displaystyle \therefore S_{ES} = 50 \times 10^3 \ (VA) = 50 \ (kVA)$

Solución d). Para una conexión como el del autotransformador, la mayoría de los resultados calculados en el inciso a se cambiarán. En el caso de la impedancia en serie por unidad, decrementará por el recíproco de la ventaja de potencia, por lo que la resistencia equivalente por unidad es

$\displaystyle R_{eq,pu} = \frac{9.635 \times 10^{-3}}{\frac{4+1}{1}}$

$\displaystyle R_{eq,pu} = 1.927 \times 10^{-3} \ (pu)$

y la reactancia equivalente por unidad es

$\displaystyle X_{eq,pu} = \frac{39.76 \times 10^{-3}}{\frac{4+1}{1}}$

$\displaystyle R_{eq,pu} = 7.952 \times 10^{-3} \ (pu)$

Para la rama de excitación, los valores de cada uno de sus elementos, no se alteran, es decir,

$R_{C,pu} = 16.44 \ (pu)$ y $X_{M,pu} = 3.321 \ (pu)$

En condiciones nominales y con un factor de potencia unitario, la potencia de entrada será de $P_{ent} = 1 \ (pu)$ . Así que, para determinar la potencia de salida, se debe tomar en cuenta la potencia de entrada, la potencia por pérdidas en el núcleo

$\displaystyle P_{nucleo} = \frac{V^2}{R_{C,pu}}$