Introducción a la electrónica de potencia. Problema 10. Máquinas eléctricas.

Problema. Un circuito recortador de conmutación forzada con condensador en serie alimenta una carga puramente resistiva como se muestra en la figura.

$V_{DC} =120 \ (V)$	$R = 30 \ (k \Omega)$
$I_H = 6 \ (mA)$	$R_{carga} = 250 \ (\Omega)$
$V_{BO} = 200 \ (V)$	$C = 100 \ (\mu F)$

Figura 3.10.1 Circuito recortador de conmutación forzada con condensador en serie.

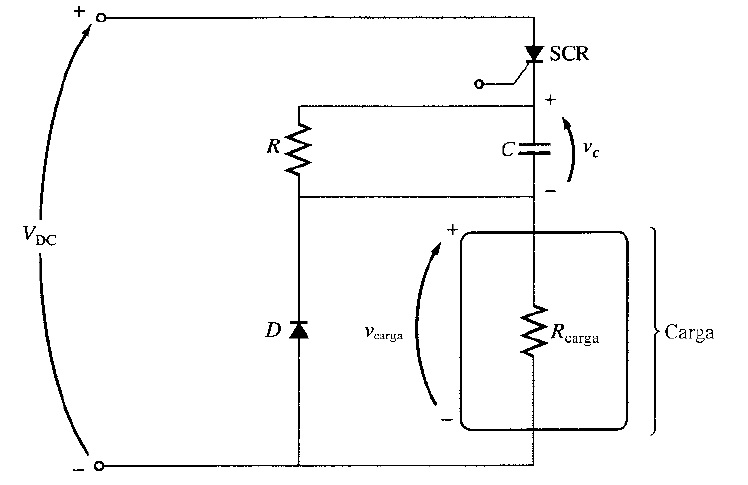
a) Si se enciende el SCR, ¿cuánto tiempo permanecerá encendido? ¿Por qué se apagará?

b) Si se apaga el SCR, ¿cuánto tiempo transcurrirá hasta que el SCR pueda ser encencido de nuevo? (Suponga que deben pasar tres constantes de tiempo antes de que el condensador se descarge.)

c) ¿Qué dificulta o dificultades revelan estos cálculos acerca de este circuito recortador sencillo de conmutación forzada con condesador en serie?

d) ¿Cómo se puede eliminar la(s) dificultad(es) descrita(s) en el inciso c)?

Solución a). Cuando el SCR esté encendido, permanecerá encendido hasta que la corriente a través de él descienda por debajo de $I_H$ . Esto ocurre cuando el capacitor se cargue hasta un voltaje suficientemente alto para reducir la corriente por debajo de $I_H$ . Si se ignora la resistencia (porque es mucho más grande que $R_{carga}$ ), el capacitor carga a través del resistor $R_{carga}$ con una constante de tiempo

$\displaystyle \tau_{carga} = R_{carga} C$

$\displaystyle \tau_{carga} = (250 \ \Omega)(150 \times 10^{-6} F)$

$\displaystyle \tau_{carga} = 0.0375 \ (s)$

La ecuación para el voltaje en el capacitor como una función del tiempo durante la parte de carga del ciclo es (utilizando la ley de corriente de Kirchhoff)

$\displaystyle \sum{i} = 0$

$\displaystyle \frac{v_C-V_{DC}}{R_{carga}} + C \frac{dv_c}{dt}= 0$

$\displaystyle \frac{v_C}{R_{carga}} - {V_{DC}}{R_{carga}} + C \frac{dv_c}{dt}= 0$

$\displaystyle \frac{v_C}{R_{carga}C} - {V_{DC}}{R_{carga}C} + \frac{dv_c}{dt}= 0$

$\displaystyle \frac{dv_C}{dt} + \frac{1}{R_{carga}C} v_C = \frac{V_{DC}}{R_{carga}C}$

Resolviendo por factor integrante

$\displaystyle v_C (t) = V_{DC} + A e^{- \frac{1}{R_{carga} C} t}$

Tomando la condición inicial $v_C (0) = 0$ , el valor de $A$ es

$\displaystyle v_C (0) = V_{DC} + A e^{- \frac{1}{R_{carga} C} (0)}$

$\displaystyle 0 = V_{DC} + A$

$\displaystyle A = - V_{DC}$

Entonces

$\displaystyle v_C (t) = V_{DC} - V_{DC} e^{- \frac{1}{R_{carga} C} t}$

La corriente a través del capacitor es

$\displaystyle i_C (t) = C \frac{dv_C}{dt}$

$\displaystyle i_C (t) = C \frac{d}{dt} \left[ V_{DC} - V_{DC} e^{- \frac{1}{R_{carga} C} t} \right]$

$\displaystyle i_C (t) = \frac{V_{DC}}{R_{carga}} e^{- \frac{1}{R_{carga} C} t}$

Despejando $t$ , resulta

$\displaystyle t = - R_{carga} C \ln{\left(\frac{R_{carga} \cdot i_C}{V_{DC}} \right)}$

La corriente a través del SCR consiste de la corriente a través del resistor $R$ más la corriente a través del capacitor. La corriente a través del resistor $R$ es

$\displaystyle I_R = \frac{120 \ (V)}{20 \ (k\Omega)} = 4 \ (mA)$

y la corriente de mantenimiento del SCR es de 6 (mA), provocando que el SCR se apague cuando la corriente a través del capacitor disminuya a 2 (mA). La corriente en el tiempo

$\displaystyle t = - R_{carga} C \ln{\left(\frac{R_{carga} \cdot i_C}{V_{DC}} \right)}$

$\displaystyle t = - (250)(100 \times 10^{-6}) \ln{\left[\frac{(250)(2 \times 10^{-3})}{120} \right]}$

$\therefore t = 0.137 \ (s)$

Solución b). El SCR puede estar encendido una vez más el capacitor se ha descargado. El capacitor se descarga a través del resistor $R$ . Puede ser considerado para estar completamente descargado después de tres constantes de tiempo. Ya que

$\tau = RC$

$\tau = (30 \times 10^3)(100 \times 10^{-6})$

$\tau = 3 (s)$

Por lo que el SCR estará listo para disparar otra vez después de 9 segundos.

Solución c). En este circuito, el tiempo de encendido es mucho más corto que el resto del tiempo para el SCR, por lo que la potencia puede fluir a la carga solo a una fracción muy pequeña de tiempo. (Este efecto sería menos exagerado si el radio de $R$ a $R_{carga}$ fuera más pequeño).

solución d). Este problema puede ser eliminado usando un circuito de conmutación en serie más complejo. Estos circuitos complejos proporcionan rutas especiales para descargar rápidamente el capacitor, de tal modo que el circuito pueda ser disparado lo más pronto posible.

Introducción a la electrónica de potencia. Problema 10. Máquinas eléctricas.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Introducción a la electrónica de potencia. Problema 10. Máquinas eléctricas.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta