Introducción a la electrónica de potencia. Problema 11. Máquinas eléctricas.

Problema. Un circuito recortador de conmutación forzada con un condensador en paralelo alimenta una carga puramente resistiva, como se muestra en la figura.

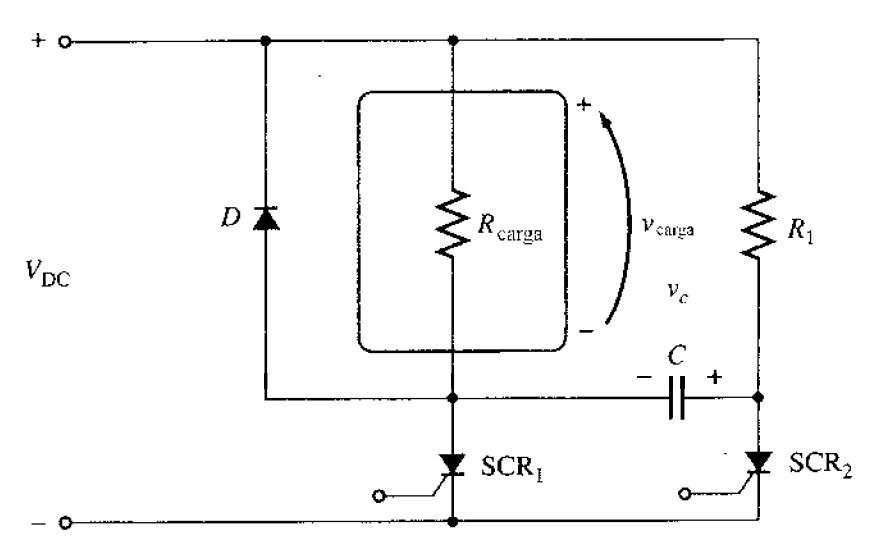
a) Si se enciende , ¿cuánto tiempo permanecerá encendido? ¿Por qué causa se apaga?

b) ¿Cuál es el menor tiempo para que pueda apagarse luego de haber sido encendido? (Suponga que deben transcurrir tres constantes de tiempo antes que el condensador esté cargado).

c) Si se apaga , ¿cuánto tiempo debe transcurrir hasta que el SCR pueda volver a ser encendido?

d) ¿Qué dificultad o dificultades revelan estos cálculos sobre éste sencillo circuito recortador de conmutación forzada con condensador en paralelo?

e) ¿Cómo se puede(n) eliminar la(s) dificultades(s) descrita(s) en el inciso d)?

Solución a). Cuando el se encienda, permanece encendido indefinidamente hasta que sea forzado a apagarse. Cuando esté encendido, el condensador se carga hasta volts con la polaridad mostrada en la figura 3.11.1. Una vez de que esté cargado, el puede apagarse en algún tiempo por el disparo del . Cuando el haya disparado, el voltaje a través de él disminuya instantáneamente alrededor de 0 (V), que forza al voltaje en el ánodo del para ser volts, apagando al . (Se observa que el se apagará espontáneamente después de que se descargue el capacitor, ya que para el .

Solución b). Si se asume que el condensador debe estar totalmente cargado antes de que el sea forzado a apagarse, entonces el tiempo requerido sería el tiempo para cargar al condensador. El condensador carga a través del resistor y la constante de tiempo para la carga es

Si se asume que esto toma tres constantes de tiempo para cargar completamente al condensador, entonces el tiempo hasta que pueda ser apagado es de 0.9 (s). (Note que esto no es una suposición realista. En la vida real, es posible apagar el con menos de un voltaje de lleno a través del condensador.)

Solución c). El puede estar encendido nuevamente después de que el condensador se cargue y el se apague. El condensador se carga a través de , por lo que la constante de tiempo de carga es

y el se apagará en unos pocos milisegundos.

Solución d). En este circuito, una vez de que el dispare, un periodo substancial de tiempo debe pasar antes de que la energía a la carga pueda ser apagado. Si la energía para la carga debe estar encendida y apagada rápidamente, este circuito no debería hacer el trabajo.

Solución e). Este problema puede ser eliminado usando uno de los circuitos de conmutación compleja en paralelo. Estos circuitos más complejos proporcionan rutas especiales para cargar rápidamente al capacitor, tal que el circuito pueda apagarse rápido después de que se encendió.