El cono sumergido en la arena. Razón de cambio. Aplicaciones de cálculo diferencial.

Problema. Una pieza de forma de cono circular recto y cuyo ángulo en el vértice inferior es de 30° se sumerge en la arena de una playa a una velocidad constante de 2 (cm/seg), siendo el eje del cono perpendicular a la superficie de la arena, la cual es plana y horizontal.

¿A qué velocidad desaparece la superficie lateral de la pieza en la arena cuando el extremo o vértice está a 10 (cm) por debajo de la superficie de la arena?

*Figura 3.6.1 Representación gráfica del problema.*

Solución. Se observa que

*Figura 3.6.2 Análisis trigonométrico del cono.*

Para determinar la velocidad en que desaparecerá la superficie lateral del cono se toma en cuenta el área lateral del cono

$A = \pi r \ell$

Por lo que su superficie lateral es

$S= \pi r \ell$

Para determinar $\ell$ se utiliza teorema de Pitágoras

$\displaystyle h^2 + r^2 = \ell^2$

$\displaystyle \sqrt{h^2+r^2} = \ell$

$\displaystyle \ell = \sqrt{h^2+r^2}$

*Figura 3.6.4 Análisis trigonométrico del cono.*

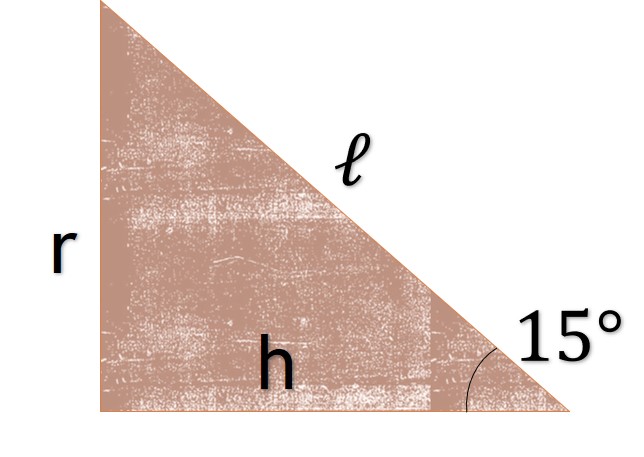
Una vez más, en el triángulo rectángulo, se utilizan las identidades trigonométricas para reemplazar el equivalente del radio “ $r$ ”

$\displaystyle \tan{15} = \frac{r}{h}$

$\displaystyle r = h \tan{15}$

Realizando la sustitución de ℓ y $r$ en la ecuación de la superficie lateral de cono

$S = \pi r \ell$

$\displaystyle S = \pi r \sqrt{h^2+r^2}$

$\displaystyle S = \pi (h \tan{15}) \sqrt{h^2+(h \tan{15})^2}$

$\displaystyle S = \pi (h \tan{15}) \sqrt{h^2+h^2 \tan^2{15}}$

$\displaystyle S = (\pi \tan{15}) (h) \sqrt{h^2 (1+\tan^2{15})}$

$\displaystyle S = (\pi \tan{15}) (h) h \sqrt{1+\tan^2{15}}$

$\displaystyle S = (\pi \tan{15}) h^2 \sqrt{1 + \tan^2{15}}$

Usando la identidad trigonométrica $1+\tan^2{15} = \sec^2{15}$ y sustituyendo

$\displaystyle S = (\pi \tan{15}) h^2 \sqrt{\sec^2{15}}$

$\displaystyle S = (\pi \tan{15}) h^2 \sec{15}$

$\displaystyle S = \pi \tan{15} \cdot \sec{15} \cdot h^2$

Donde este resultado representa la ecuación estática.

Derivando en ambos miembros con respecto a $t$

$\displaystyle \frac{dS}{dt} = \frac{d}{dt} (\pi \tan{15} \cdot \sec{15} \cdot h^2)$

$\displaystyle \frac{dS}{dt} = \pi \tan{15} \sec{15} \cdot \frac{d}{dt} (h^2)$

$\displaystyle \frac{dS}{dt} = \pi \tan{15} \sec{15} (2h \frac{dh}{dt})$

$\displaystyle \frac{dS}{dt} = 2\pi \tan{15} \sec{15} \cdot h \frac{dh}{dt}$

Por lo que esta es la ecuación cinemática.

Para obtener el resultado deseado, se utilizan los valores $h=10$ y $\displaystyle \frac{dh}{dt} = 2$

$\displaystyle \frac{dS}{dt} = 2\pi \tan{15} \sec{15} \cdot h \frac{dh}{dt}$

$\displaystyle \frac{dS}{dt} = 2\pi \tan{15} \sec{15} \cdot (10)(2)$

$\displaystyle \frac{dS}{dt} = 80\pi \tan{15} \sec{15}$

$\displaystyle \frac{dS}{dt} = 80\pi \tan{15} \cdot \frac{1}{\cos{15}}$

$\displaystyle \frac{dS}{dt} \approx 34.859 \ (cm^2/seg)$

Por lo tanto, la superficie lateral del cono desaparece de la arena a razón de 34.859 $(cm^2/seg)$ .

El cono sumergido en la arena. Razón de cambio. Aplicaciones de cálculo diferencial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

El cono sumergido en la arena. Razón de cambio. Aplicaciones de cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta