Problema. Se vierte agua en un recipiente hemisférico de 40 (cm) de diámetro a razón de 10 (cm^3/seg). Calcular a qué velocidad se eleva el nivel del líquido cuando está a la profundidad del hemisferio.

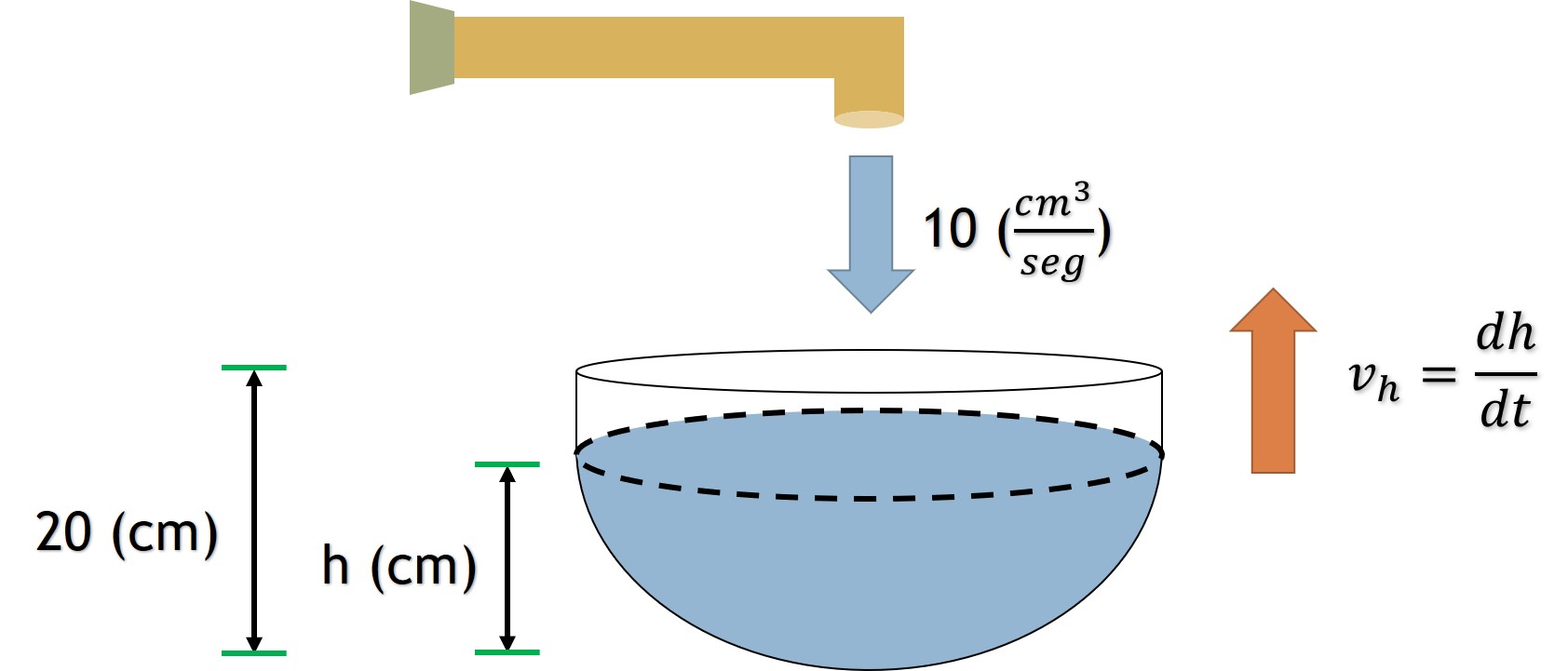
Figura 3.7.1 Representación gráfica del problema.

Solución. El volumen de un casquete esférico es

\displaystyle V = \pi (rh^2 - \frac{1}{3} h^3 )

Si el diámetro del recipiente hemisférico es de 40 (cm), su radio será de

\displaystyle r = \frac{d}{2} = \frac{40 \ (cm)}{2}

r = 20 \ (cm)

Sustituyendo este resultado en la ecuación del volumen

\displaystyle V = \pi (rh^2 - \frac{1}{3} h^3)

\displaystyle V = \pi (20h^2 - \frac{1}{3} h^3 )

\displaystyle V = 20\pi h^2 - \frac{1}{3} \pi h^3

La cual representa la ecuación estática.

Derivando en ambos miembros con respecto a “t”

\displaystyle \frac{dV}{dt} = \frac{d}{dt} (20 \pi h^2 - \frac{1}{3} \pi h^3 )

\displaystyle \frac{dV}{dt} = 20\pi \frac{d}{dt} (h^2 ) - \frac{1}{3} \pi \frac{d}{dt} (h^3 )

\displaystyle \frac{dV}{dt} = 20\pi (2h) \frac{dh}{dt} - \frac{1}{3} \pi (3h^2 ) \frac{dh}{dt}

\displaystyle \frac{dV}{dt} = 40\pi h \frac{dh}{dt} - \pi h^2 \frac{dh}{dt}

\displaystyle \frac{dV}{dt} = (40 \pi h - \pi h^2 ) \frac{dh}{dt}

Despejando “\displaystyle \frac{dh}{dt}”

\displaystyle \frac{dV}{dt} = (40\pi h - \pi h^2 ) \frac{dh}{dt}

\displaystyle \frac{\frac{dV}{dt}}{40\pi h - \pi h^2} = \frac{dh}{dt}

\displaystyle \frac{dh}{dt} = \frac{\frac{dV}{dt}}{40\pi h - \pi h^2}

Esta es la ecuación cinemática que representa la velocidad de elevación del líquido del recipiente hemisférico.

Para obtener el resultado final, se sustituyen los siguientes datos \displaystyle \frac{dV}{dt} = 10 \ (\frac{cm^3}{seg}) y h=20

\displaystyle \frac{dh}{dt} = \frac{\frac{dV}{dt}}{40\pi h - \pi h^2}

\displaystyle \frac{dh}{dt} = \frac{10}{40\pi (20) - \pi (20)^2}

\displaystyle \frac{dh}{dt} = \frac{1}{800\pi - 400\pi} = \frac{10}{400\pi}

\displaystyle \frac{dh}{dt} = 0.008 \ (cm/seg)

Realizando la conversión de “segundos” a “minutos” en el último resultado

\displaystyle \frac{dh}{dt} = 0.008 \ (cm/seg)

\displaystyle \frac{dh}{dt} = (0.008 \ cm/seg) \left( \frac{60 \ seg}{1 \ min} \right)

\displaystyle \frac{dh}{dt} \approx 0.48 \ (cm/min)

Por lo tanto, el nivel del agua se eleva a razón de 0.48 (cm/min).

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.