La cinta transportadora y el cono. Razón de cambio. Aplicaciones de cálculo diferencial.

Problema. Una cinta transportadora vierte arena en un piso horizontal formando un montó de forma cónica en el que por el coeficiente interno de rozamiento de los granos siempre la altura es igual a la tercera parte del diámetro de la base. Si la cinta descarga arena a razón de 720 ( $dm^3/min$ ) y la salida del unto de descarga está a 5 (dm) sobre el nivel del piso, calcular la velocidad de variación de la altura del cono en el momento de que alcanza el nivel del orificio.

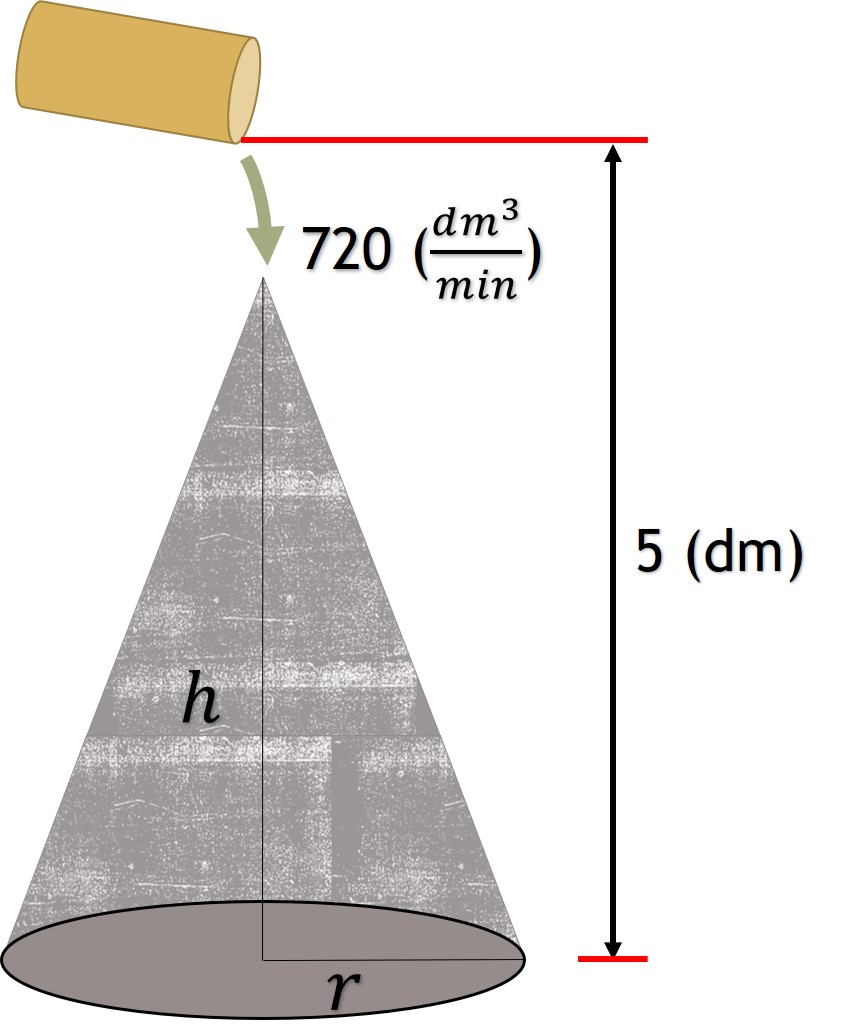
Solución. Se determina la altura del cono tomando el coeficiente interno de rozamiento de los granos de la arena, y es

$\displaystyle h = \frac{1}{3} d$

$\displaystyle h = \frac{1}{3} (2r)$

$\displaystyle h = \frac{2}{3} r$

Despejando “ $r$ ”

$\displaystyle r = \frac{3}{2} h$

Después, se determina la ecuación estática por medio de la ecuación del volumen del cono

$\displaystyle V = \frac{1}{3} \pi r^2 h$

Si $\displaystyle r = \frac{3}{2} h$ , sustituyéndolo en la ecuación del volumen

$\displaystyle V = \frac{1}{3} \pi r^2 h$

$\displaystyle V = \frac{1}{3} \pi (\frac{3}{2} h)^2 h$

$\displaystyle V = \frac{1}{3} \pi (\frac{9}{4} h^2 )h$

$\displaystyle V = \frac{1}{3} \pi (\frac{9}{4} h^3 )$

$\displaystyle V = \frac{3}{4} \pi h^3$

Esto representa la ecuación estática en donde solo depende de la altura del cono.

Derivando en ambos miembros con respecto a “ $t$ ”

$\displaystyle V = \frac{3}{4} \pi h^3$

$\displaystyle \frac{dV}{dt} = \frac{d}{dt} (\frac{3}{4} \pi h^3)$

$\displaystyle \frac{dV}{dt} = \frac{3}{4} \pi \frac{d}{dt} (h^3)$

$\displaystyle \frac{dV}{dt} = \frac{3}{4} \pi (3h^2) \frac{dh}{dt} \frac{dV}{dt} = \frac{9}{4} \pi h^2 \frac{dh}{dt}$

Despejando “ $\displaystyle \frac{dh}{dt}$ ”

$\displaystyle \frac{dV}{dt} = \frac{9}{4} \pi h^2 \frac{dh}{dt}$

$\displaystyle \frac{\frac{dV}{dt}}{\frac{9}{4} \pi h^2} = \frac{dh}{dt}$

$\displaystyle \frac{dh}{dt} = \frac{\frac{dV}{dt}}{\frac{9}{4} \pi h^2}$

Y este resultado representa la ecuación cinemática.

Para obtener el resultado deseado se toman los siguientes datos $h=5$ y $\displaystyle \frac{dV}{dt} = 720 \ (\frac{dm^3}{min})$ , y sustituyendo en la ecuación cinemática

$\displaystyle \frac{dh}{dt} = \frac{\frac{dV}{dt}}{\frac{9}{4} \pi h^2}$

$\displaystyle \frac{dh}{dt} = \frac{720}{\frac{9}{4} \pi (5)^2}$

$\displaystyle \frac{dh}{dt} \approx 4.074 \ (dm/min)$

Por lo tanto, la altura del cono formado por la arena se eleva a razón de 4.074 (dm/min).

La cinta transportadora y el cono. Razón de cambio. Aplicaciones de cálculo diferencial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

La cinta transportadora y el cono. Razón de cambio. Aplicaciones de cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta