Problema. La resistencia a la flexión de una viga de madera de sección rectangular y de una longitud dada, es proporcional al producto de su anchura por el cuadrado de su altura. Determinar las dimensiones de la viga más resistente que pueda obtenerse al maquinar un tronco de forma cilíndrica de 50 (cm) de diámetro.

Figura 4.2.1 Viga de madera con sección rectangular y de longitud dada.

Solución.

Paso 1. Por el enunciado, la resistencia de la viga es

R \varpropto (\mathrm{ancho}) (\mathrm{altura})^2

R = kxy^2

Paso 2. En la figura del problema, se observa en el triángulo rectángulo

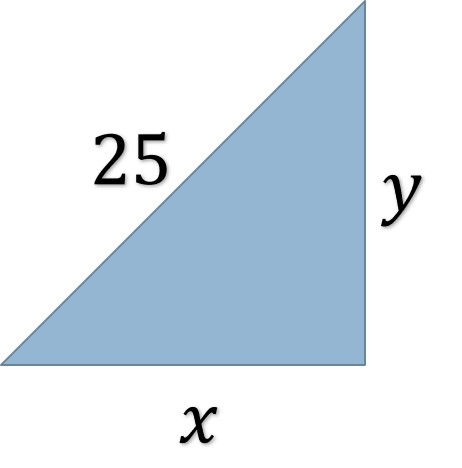
Figura 4.2.1 Triángulo rectángulo obtenido de la viga de madera.

Por medio del teorema de Pitágoras

x^2+y^2=50^2

x^2+y^2=2500

Despejando “y”

\displaystyle y = \sqrt{2500-x^2}

Y esta dada en (cm^2).

Paso 3. Sustituyendo en “y” en la ecuación de la resistencia de la viga

R = k x y^2

\displaystyle R = k x(\sqrt{2500-x^2})^2

R = k x (2500-x^2)

R = k (2500x - x^3)

Paso 4. Derivando esta ecuación con respecto a “x”

\displaystyle \frac{dR}{dx} = \frac{d}{dx} [k (2500x - x^3)]

\displaystyle \frac{dR}{dx} = k \left[\frac{d}{dx} (2500x) - \frac{d}{dx} (x^3) \right]

\displaystyle \frac{dR}{dx} = k [(2500) - (3x^2)]

\displaystyle \frac{dR}{dx} = k(2500 - 3x^2)

Paso 5. Si \displaystyle \frac{dR}{dx} es nula

\displaystyle \frac{dR}{dx} = k(2500 - 3x^2)

0 = k (2500 - 3x^2)

0 = 2500 - 3x^2

3x^2 = 2500

\displaystyle x^2 = \frac{2500}{3}

\displaystyle \therefore x = \sqrt{\frac{2500}{3}} = \frac{50}{\sqrt{3}}

Paso 6. Sustituyendo en la siguiente ecuación

\displaystyle y = \sqrt{2500-x^2}

\displaystyle y = \sqrt{2500-(\frac{50}{\sqrt{3}})^2}

\displaystyle y = \sqrt{2500- \frac{2500}{3}}

\displaystyle \therefore y = \frac{50\sqrt{2}}{\sqrt{3}}

Paso 7. Derivando nuevamente en la función

\displaystyle \frac{d}{dx} \left(\frac{dR}{dx} \right) = \frac{d}{dx} [k(2500-3x^2)]

\displaystyle \frac{d^2 R}{dx^2} = k \left[\frac{d}{dx} (2500) - 3 \frac{d}{dx} (x^2) \right]

\displaystyle \frac{d^2 R}{dx^2} = k (0 - 6x)

\displaystyle \frac{d^2 R}{dx^2} = -6kx

Si \displaystyle x = \frac{50}{\sqrt{3}}

\displaystyle \frac{d^2 R}{dx^2} = -6k \left(\frac{50}{\sqrt{3}} \right) = -\frac{300}{\sqrt{3}}k

Como el resultado de \displaystyle \frac{d^2 R}{dx^2} < 0 se trata de un máximo. Así que, por tanto, si el ancho es de \displaystyle \frac{50}{\sqrt{3}} \ (cm) y la es de \displaystyle \frac{50\sqrt{2}}{\sqrt{3}} \ (cm), la resistencia de la viga es máxima.

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.