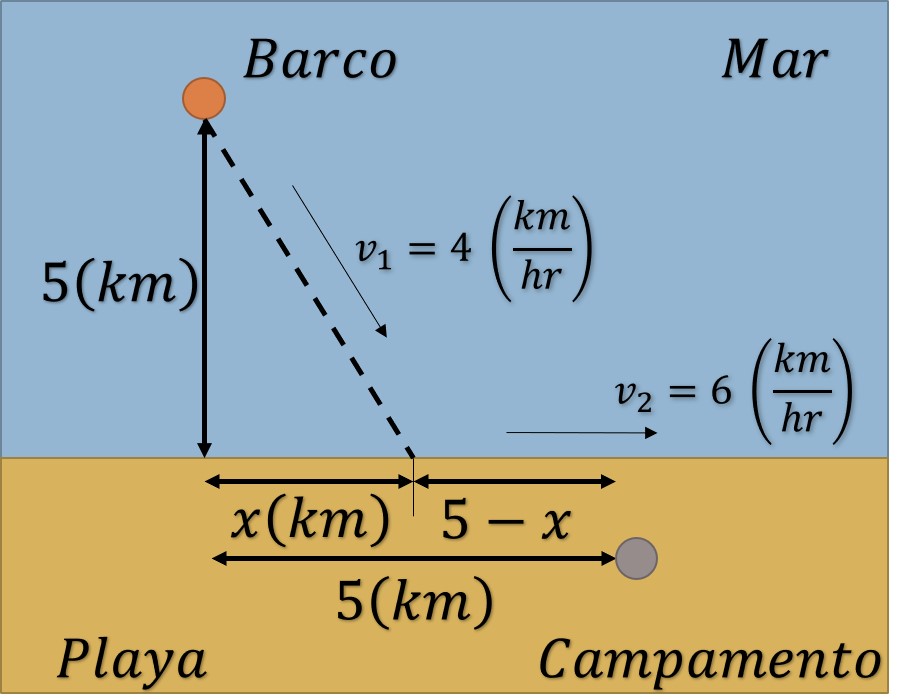
El barco, el pasajero y la playa. Máximos y mínimos. Aplicaciones de cálculo diferencial.

Problema. Hay un barco anclado a 5 (km) del punto más cercano a una playa rectilínea. Se desea enviar un pasajero hasta un campamento situado a 5 (km) a lo largo de la playa a partir del punto más próximo al barco. El pasajero puede remar a razón de 4 (km/hr) y caminar por la arena de la playa a 6 (km/hr) ¿Cuál será el tiempo más corto posible de viaje del barco al campamento?

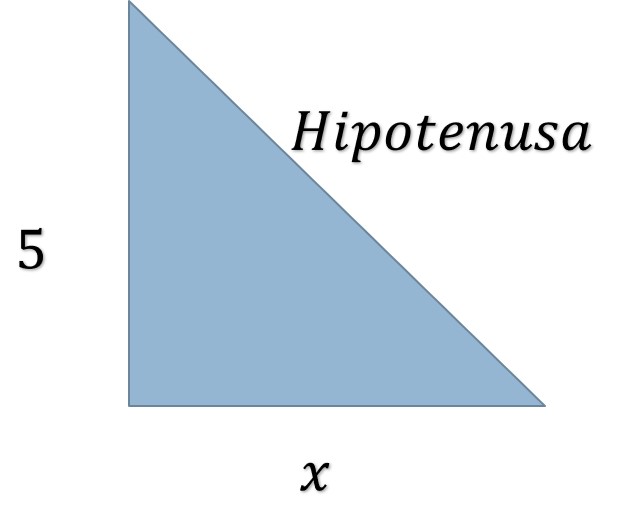
*Figura 4.4.1 Representación gráfica del problema.*

Solución. Por medio del triángulo rectángulo y del teorema de Pitágoras, se determina la hipotenusa.

$\displaystyle \mathrm{Hipotenusa} = \sqrt{x^2+5^2}$

$\displaystyle d_1 = \sqrt{x^2+25}$

*Figura 4.4.2 Triángulo rectángulo desarrollado por la figura 4.4.1*

El tiempo de remado es

$\displaystyle v_1 = \frac{d_1}{t_1}$

$\displaystyle t_1 = \frac{d_1}{v_1}$

$\displaystyle t_1 = \frac{\sqrt{x^2+25}}{4}$

*Figura 4.4.3 Descripción de la trayectoria de la persona que rema.*

El tiempo caminado del pasajero es

$\displaystyle v_2 = \frac{d_2}{t_2}$

$\displaystyle t_2 = \frac{d_2}{v_2}$

$\displaystyle t_2 = \frac{(5-x)}{6}$

*Figura 4.4.4 Descripción de la trayectoria de la persona que camina.*

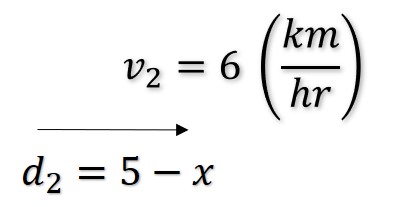
Paso 1. La suma del tiempo de remado y el tiempo caminado del pasajero es el tiempo empleado.

$t = t_1 + t_2$

$\displaystyle t = \frac{\sqrt{x^2+25}}{4} + \frac{(5-x)}{6}$

Donde “ $t$ ” está dada en (hr).

Paso 2. Derivando la función del tiempo con respecto a “ $x$ ” en ambos miembros

$\displaystyle \frac{dt}{dx} = \frac{d}{dx} \left(\frac{\sqrt{x^2+25}}{4} \right) + \frac{(5-x)}{6}$

$\displaystyle \frac{dt}{dx} = \frac{d}{dx} \left(\frac{\sqrt{x^2+25}}{4} \right) + \frac{d}{dx} \left[ \frac{(5-x)}{6} \right]$

$\displaystyle \frac{dt}{dx} = \frac{1}{4} \frac{d}{dx} \left(\sqrt{x^2+25} \right) + \frac{1}{6} \frac{d}{dx} (5-x)$

$\displaystyle \frac{dt}{dx} = \frac{1}{4} \left[ \frac{1}{2\sqrt{x^2+25}} \frac{d}{dx} (x^2 + 25) \right] + \frac{1}{6} (0-1)$

$\displaystyle \frac{dt}{dx} = \frac{1}{4} \left[\frac{1}{2 \sqrt{x^2+25}} (2x) \right] + \frac{1}{6} (-1)$

$\displaystyle \frac{dt}{dx} = \frac{1}{4} \left(\frac{x}{\sqrt{x^2+25}} \right) - \frac{1}{6}$

$\displaystyle \frac{dt}{dx} = \frac{x}{4 \sqrt{x^2+25}} - \frac{1}{6}$

Paso 3. Si $\displaystyle \frac{dt}{dx}$ es nula

$\displaystyle \frac{dt}{dx} = \frac{x}{4 \sqrt{x^2+25}} - \frac{1}{6}$

$\displaystyle 0 = \frac{x}{4\sqrt{x^2+25}} - \frac{1}{6}$

$\displaystyle \frac{1}{6} = \frac{x}{4 \sqrt{x^2+25}}$

$\displaystyle 4 \sqrt{x^2+25} = 6x$

$\displaystyle \sqrt{x^2+25} = \frac{6}{4} x$

$\displaystyle x^2 + 25 = \left(\frac{6}{4} x \right)^2$

$\displaystyle x^2 = \frac{36}{16} x^2 - 25$

$\displaystyle x^2 - \frac{36}{16} x^2 = -25$

$\displaystyle -\frac{20}{16} x^2 = -25$

$x^2=20$

$\displaystyle x = \sqrt{20}$

Paso 4. Sustituyendo el valor de “ $x$ ” en la distancia caminada por el pasajero

$\displaystyle d_2 = 5 - x$

$\displaystyle d_2 = 5 - \sqrt{20}$

$\displaystyle d_2 = 0.53 \ (km)$

Y en la ecuación del tiempo

$\displaystyle t = \frac{\sqrt{x^2+25}}{4} + \frac{(5-x)}{6}$

$\displaystyle t = \frac{\sqrt{(\sqrt{20})^2+25}}{4} + \frac{(5-\sqrt{20})}{6}$

$\displaystyle \therefore t = 1.765 \ (hr) \approx 1 \ (hr) \ 46 \ (min)$

Paso 5. Derivando nuevamente

$\displaystyle \frac{d}{dx} \left(\frac{dt}{dx} \right) = \frac{d}{dx} \left(\frac{x}{4\sqrt{x^2+25}} - \frac{1}{6} \right)$

$\displaystyle \frac{d^2 t}{dx^2} = \frac{1}{4} \frac{d}{dx} \left(\frac{x}{\sqrt{x^2+25}} \right) + \frac{d}{dx} \left(-\frac{1}{6} \right)$

$\displaystyle \frac{d^2 t}{dx^2} = \frac{25}{4(25+x^2 )^{3/2}}$

Si $\displaystyle x = \sqrt{20}$

$\displaystyle \frac{d^2 t}{dx^2} = \frac{25}{4[25 + (\sqrt{20})^2 ]^{3/2}}$

$\displaystyle \frac{d^2 t}{dx^2} = \frac{25}{4(25 + 20)^{3/2}}$

$\displaystyle \therefore \frac{d^2 t}{dx^2} = \frac{25}{4(45)^{3/2}}$

Como $\displaystyle \frac{d^2 t}{dx^2}>0$ se trata de un mínimo. Por lo tanto, el pasajero deberá desembarcar a $\displaystyle \sqrt{20} \ (km)$ a lo largo de la costa y caminar 0.53 (km) para gastar 1 (hr) 46 (min) como tiempo mínimo.

El barco, el pasajero y la playa. Máximos y mínimos. Aplicaciones de cálculo diferencial.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

El barco, el pasajero y la playa. Máximos y mínimos. Aplicaciones de cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta