Problema. Un granjero desea cercar un terreno rectangular , uno de cuyos lados coincide con la orilla de un río rectilíneo, por consiguiente, éste lado no necesita cerca. El trabajo de hechura de la cerca paralela al río tiene un costo de $200 por cada metro lineal. El granjero dispone de $900 000 para efectuar la obra. Hallar: a)Dimensiones del cercado para poder encerrar la mayor área posible. b)El perímetro de la cerca.

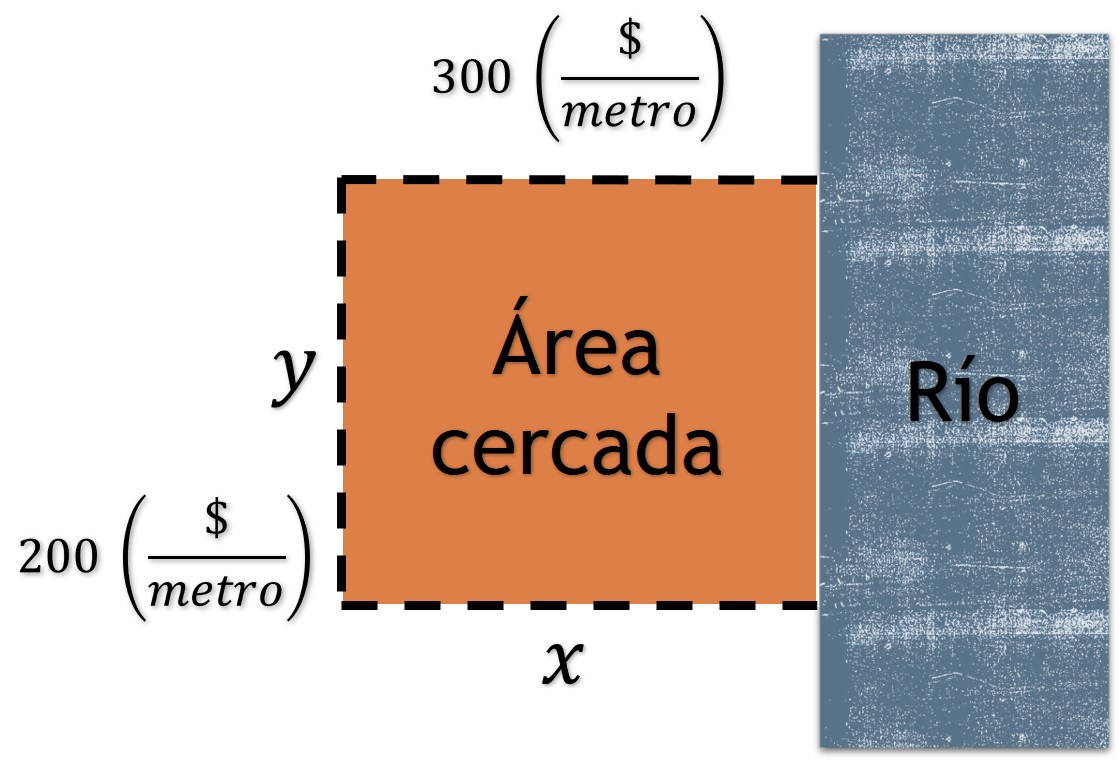
Solución.

Paso 1. Se calcula el área de la cerca

A=xy

Donde A está dada en (m^2).

Paso 2. El costo de la obra es

C=C_1+C_2

Donde C_1 es el costo de los dos lados horizontales mientras que C_2 es el costo de un lado vertical. La expresión de C_1 es

C_1 = (x + x)(300)

Y la expresión para C_2 es C_2 = y(200)

Entonces

C=C_1+C_2

900 000=(x+x)(300)+y(200)

900 000=2x(300)+200y

900 000=600x+200y

Despejando “y”

900 000=600x+200y

600x + 200y = 900 000

200y = 900 000 - 600x

\displaystyle y = \frac{900 000 - 600x}{200}

y=4500-3x

Paso 3. Sustituyendo este último resultado en la ecuación del área cerrada

A=xy

A=x(4500-3x)

A=4500x-3x^2

Solución del a). Dimensiones de la cerca.

Paso 4. Derivando el área con respecto a “x”

\displaystyle \frac{d}{dx} (A) = \frac{d}{dx} (4500x - 3x^2)

\displaystyle \frac{dA}{dx} = \frac{d}{dx} (4500x) - \frac{d}{dx} (3x^2)

\displaystyle \frac{dA}{dx} = 4500 - 6x

Paso 5. Si \displaystyle \frac{dA}{dx} es nula

0=4500-6x

6x=4500

x=750

Donde está dado en metros (m).

Sustituyendo el valor de “x” en la ecuación “y”

y=4500x-3x^2

y=4500(750)-3(750)^2

y=2250

Donde “y” está dado en metros (m).

Paso 6. Calculando la segunda derivada del área.

\displaystyle \frac{d}{dx} (\frac{dA}{dx}) = \frac{d}{dx} (4500 - 6x)

\displaystyle \frac{d^2 A}{dx^2} = -6

Como \displaystyle \frac{d^2 A}{dx^2}<0, se trata de un máximo, es decir, las dimensiones calculadas generan un mayor área posible. Por lo tanto, las dimensiones de la granja serán de 750 (m) de ancho por 2250 (m) de largo.

Solución del b). Perímetro de la cerca.

El perímetro de la cerca es

P=x+y+x

P=2x+y

P=2(750)+2250

P=3750

El perímetro de la cerca es de 3750 (m).

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Un comentario sobre “La cerca del granjero. Máximos y mínimos. Aplicaciones de cálculo diferencial.”

  1. J’aime beaucoup votre blog. Un plaisir de venir flâner sur vos pages. Une belle découverte et blog très intéressant. Je reviendrai m’y poser. N’hésitez pas à visiter mon univers. Au plaisir.

    Me gusta

    Responder

Replica a Angelilie Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.