Funciones periódicas en la transformada de Laplace. Laplace.

Introducción

Sea $f(t)$ con período $T>0$ tal que $f(t+T) = f(t)$ . Entonces

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-sT}} \int^{T}_{0}{e^{-st} f(t) \ dt}$

Problemas resueltos

Problema 1. Sea la función $\displaystyle f(t) = \left\{\begin{matrix} 2 \quad \text{para} \ 0<t < 1 \\ 0 \quad \text{para} \ 1 < t < 2 \end{matrix} \right.$ con periodo de 2. Hallar su transformada de Laplace.

Solución. Tomando la fórmula para funciones periódicas y sustituyendo, resulta

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-sT}} \int^{T}_{0}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-s(2)}} \int^{2}_{0}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-2s}} \left[\int^{1}_{0}{e^{-st} (2) \ dt} + \int^{2}_{1}{e^{-st} (0) dt} \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{2}{1-e^{-2s}}\int^{1}_{0}{e^{-st}\ dt}$

$\displaystyle \mathcal{L}[f(t)] = \frac{2}{1-e^{-2s}}\left[-\frac{1}{s} e^{-st} \right]^{1}_{0}$

$\displaystyle \mathcal{L}[f(t)] = \frac{2}{1-e^{-2s}}\left[-\frac{1}{s} e^{-s(1)} + \frac{1}{s} e^{-s(0)} \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{2}{1-e^{-2s}}\left(-\frac{1}{s} e^{-s} + \frac{1}{s} e^{0} \right)$

$\displaystyle \mathcal{L}[f(t)] = \frac{2}{1-e^{-2s}}\left[-\frac{1}{s} e^{-s} + \frac{1}{s} (1) \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{2}{1-e^{-2s}}\left(-\frac{1}{s} e^{-s} + \frac{1}{s} \right)$

$\displaystyle \mathcal{L}[f(t)] = \frac{2}{s(1-e^{-2s})}\left(-e^{-s} + 1\right)$

$\displaystyle \mathcal{L}[f(t)] = \frac{2}{s(1-e^{-s})(1+e^{-s})}\left(1-e^{-s}\right)$

$\displaystyle \mathcal{L}[f(t)] = \frac{2}{s(1+e^{-s})}$

Problema 2. Encontrar la transformada de Laplace de la siguiente función periódica

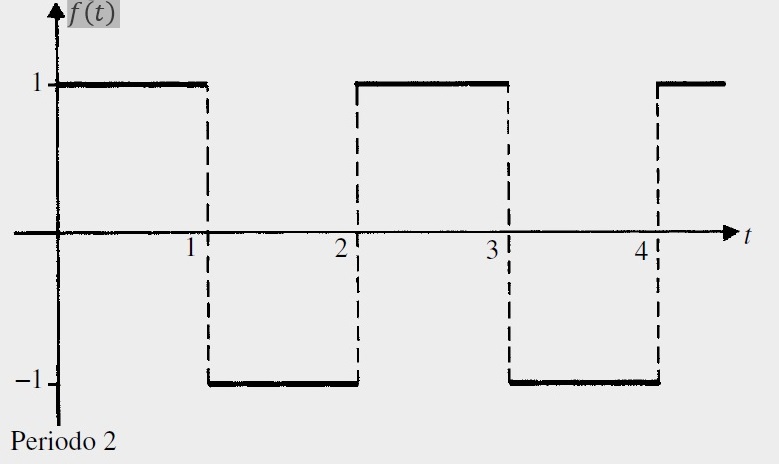
*Figura 1. Función periódica del problema 2.*

Solución. Analizando la figura, se tiene la siguiente función

$\displaystyle f(t) = \left\{\begin{matrix} 1 \quad \text{para} \ 0 <t < 1 \\ -1 \quad \text{para} \ 1 < t < 2 \end{matrix} \right.$

Tomando la formula para determinar la transformada de Laplace de $f(t)$ de la función periódica es

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-sT}} \int^{T}_{0}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-s(2)}} \int^{2}_{0}{e^{-st} f(t) \ dt}$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-2s}} \left[\int^{1}_{0}{e^{-st} (1) \ dt} + \int^{2}_{1}{e^{-st} (-1) \ dt} \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-2s}} \left[\int^{1}_{0}{e^{-st} \ dt} - \int^{2}_{1}{e^{-st} \ dt} \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-2s}} \left[\left[- \frac{1}{s} e^{-st} \right]^{1}_{0} - \left[-\frac{1}{s} e^{-st} \right]^{2}_{1} \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-2s}} \left[\left[-\frac{1}{s} e^{-s(1)} + \frac{1}{s} e^{-s(0)} \right] - \left[- \frac{1}{s} e^{-s(2)} + \frac{1}{s} e^{-s(1)} \right] \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-2s}} \left[\left[-\frac{1}{s} e^{-s} + \frac{1}{s} (1) \right] - \left[- \frac{1}{s} e^{-2s} + \frac{1}{s} e^{-s} \right] \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-2s}} \left[\left[-\frac{1}{s} e^{-s} + \frac{1}{s} \right] - \left[- \frac{1}{s} e^{-2s} + \frac{1}{s} e^{-s} \right] \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-2s}} \left(-\frac{1}{s} e^{-s} + \frac{1}{s} + \frac{1}{s} e^{-2s} - \frac{1}{s} e^{-s} \right)$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-2s}} \left(\frac{1}{s} e^{-2s} - \frac{2}{s} e^{-s} + \frac{1}{s} \right)$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{s(1-e^{-2s})} \left(e^{-2s} - 2e^{-s} + 1 \right)$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{s(1-e^{-s})(1+e^{-s})} \left(e^{-s} - 1 \right)^2$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{s(1+e^{-s})} (e^{-s} - 1)$

Finalmente

$\displaystyle \therefore \mathcal{L}[f(t)] = \frac{(e^{-s} - 1)}{s(1+e^{-s})}$

Problema 3. Hallar la transformada de Laplace para la siguiente función periódica.

*Figura 2. Función periódica del problema 3.*

Solución. Aplicando el método de punto y pendiente [sabiendo que es (0,0) y (1,1)], resulta que

$\displaystyle y-y_0 = \left(\frac{y_1 - y_0}{x_1 - x_0} \right) (x - x_0)$

Cambiando la variable $x$ por $t$ y $y$ por $f(t)$ , se expresa que

$\displaystyle f(t) - f(t_0) = \left[\frac{f(t_1) - f(t_0)}{t_1 - t_0} \right] (t - t_0)$

Sustityendo

$\displaystyle f(t)-0 = \left(\frac{1 - 0}{1 - 0} \right) (t - 0)$

$\displaystyle f(t) = \left(\frac{1}{1} \right) (t)$

$\displaystyle f(t) = (1) (t)$

$\displaystyle f(t) = t$

Ahora, tomando la fórmula para determinar la transformada de Laplace de una función periódica

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-sT}} \int^{T}_{0}{e^{-st} f(t) \ dt}$

Sustituyendo

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-s(1)}} \int^{1}_{0}{e^{-st} (t) \ dt}$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-s}} \int^{1}_{0}{t e^{-st} \ dt}$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-s}} \left[-\frac{1}{s} t e^{-st} - \frac{1}{s^2} e^{-st} \right]^{1}_{0}$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-s}} \left[\left(-\frac{1}{s} (1) e^{-s(1)} - \frac{1}{s^2} e^{-s(1)} \right) - \left(-\frac{1}{s} (0) e^{-s(0)} - \frac{1}{s^2} e^{-s(0)} \right) \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-s}} \left[\left(-\frac{1}{s} e^{-s} - \frac{1}{s^2} e^{-s} \right) - \left(0 - \frac{1}{s^2} e^{0} \right) \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-s}} \left[\left(-\frac{1}{s} e^{-s} - \frac{1}{s^2} e^{-s} \right) - \left(- \frac{1}{s^2}(1) \right) \right]$

$\displaystyle \mathcal{L}[f(t)] = \frac{1}{1-e^{-s}} \left[\left(-\frac{1}{s} e^{-s} - \frac{1}{s^2} e^{-s} \right) - \left(- \frac{1}{s^2} \right) \right]$