Aplicaciones a circuitos eléctricos y la transformada de Laplace. Laplace.

Introducción

Un circuito eléctrico sencillo consta de los siguientes elementos de un circuito conectados en serie con un interruptor $k$ :

Un generador o batería que produce una fuerza electromotriz (f.e.m.) E (en volts).
Una resistencia R (en ohms).
Un inductor que tiene una inductancia L (en henrys).
Un condesador con capacitancia C (en faradios).

Los elementos de un circuito se representan simbólicamente en la figura 1.

Figura 3.2.1 — *Figura 1. Representación simbólica de un circuito RLC.*

Cuando se baja el interruptor, el circuito estará cerrado y fluirá una carga $Q$ dada en (columbios) a las placas del capacitor. La razón de tiempo de la carga del flujo, dada por $\displaystyle \frac{dQ}{dt} = I$ , se llama la corriente y se mide en amperios cuando $t$ se mide en segundos.

Un problema importante es el determinar las cargas de los condensadores y las corrientes en función del tiempo. Para esto se ha definido la caída de potencial (caída de voltaje) a través de un elemento del circuito.

a) Caída de voltaje a través de una resistencia: $\displaystyle v_R = R \cdot I = R \frac{dQ}{dt}$

b) Caída de voltaje a través de un inductor: $\displaystyle v_L = L \frac{dI}{dt} = L \frac{d^2Q}{dt^2}$

c) Caída de voltaje a través de un capacitor: $v_C = \frac{Q}{C}$

d) Caída de voltaje a través de un generador: $- \text{Subida de voltaje} = -E$

Para hallar la ecuación diferencial de un circuito, es necesario utilizar las leyes de Kirchhoff:

1.- La suma algebraica de las corrientes que fluyen a través de un punto de unión es igual a cero.

$\displaystyle \sum_{k=0}^{n}{i_k} = 0$

2.- La suma algebraica de las caídas de voltaje alrededor de cualquier malla cerrada es igual a cero.

$\displaystyle \sum_{k=0}^{n}{v_k} = 0$

Problemas resueltos

Problema 1. Un inductor de 2 henrys, una resistencia de 16 ohmios y un condensador de 0.02 faradios se conectan en serie con una f.e.m. de $E$ voltios. En $t=0$ tanto la carga del condensador como la corriente del circuito valen cero. Encontrar la carga y la corriente en cualquier tiempo $t>0$ si (a) $E=300$ (voltios), (b) $E = 100 \sin{3t}$ (voltios).

Solución. Sean $q$ e $i$ respectivamente la carga y la corriente instantáneas en el tiempo $t$ . Aplicando la ley de Kirchhoff,

$\displaystyle v_L + v_R + v_C - E = 0$

$\displaystyle L \frac{di}{dt} + Ri(t) + \frac{q(t)}{C} - E = 0$

$\displaystyle \frac{di}{dt} + \frac{R}{L} i(t) + \frac{q(t)}{LC} - \frac{E}{L} = 0$

Sabiendo que $\displaystyle i(t) = \frac{dq}{dt}$ , al sustituirlo se tiene que

$\displaystyle \frac{d^2 q}{{dt}^2} + \frac{R}{L} \frac{dq}{dt} + \frac{q(t)}{LC} - \frac{E}{L} = 0$

$\displaystyle \frac{d^2 q}{{dt}^2} + \frac{R}{L} \frac{dq}{dt} + \frac{1}{LC} q(t) - \frac{E}{L} = 0$

Sustituyendo los valores

$\displaystyle \frac{d^2 q}{{dt}^2} + \frac{16}{2} \frac{dq}{dt} + \frac{1}{(2)(0.02)} q(t) - \frac{E}{2} = 0$

$\displaystyle \frac{d^2 q}{{dt}^2} + 8 \frac{dq}{dt} + 25 q(t) - \frac{E}{2} = 0$

sin olvidar las condiciones $q(0) = 0$ y $i(0) = q'(0) = 0$ .

Solución (a). Cuando $E=300$ voltios

$\displaystyle \frac{d^2 q}{{dt}^2} + 8 \frac{dq}{dt} + 25 q(t) - \frac{300}{2} = 0$

$\displaystyle \frac{d^2 q}{{dt}^2} + 8 \frac{dq}{dt} + 25 q(t) - 150 = 0$

$\displaystyle \frac{d^2 q}{{dt}^2} + 8 \frac{dq}{dt} + 25 q(t) = 150$

Aplicando la transformada de Laplace en ambos miembros,

$\displaystyle \mathcal{L} \left[\frac{d^2 q}{{dt}^2} + 8 \frac{dq}{dt} + 25 q(t) \right] = \mathcal{L} [150]$

$\displaystyle \mathcal{L} \left[\frac{d^2 q}{{dt}^2} \right] + 8 \mathcal{L} \left[\frac{dq}{dt}\right] + 25 \mathcal{L} \left[q(t) \right] = \mathcal{L} [150]$

$\displaystyle [s^2 Q(s) - s q(0) - q'(0)] + 8 [sQ(s) - q(0) ] + 25 Q(s) = \frac{150}{s}$

Continuando

$\displaystyle [s^2 Q(s) - s (0) - (0)] + 8 [sQ(s) - (0) ] + 25 Q(s) = \frac{150}{s}$

$\displaystyle s^2 Q(s) + 8s Q(s) + 25 Q(s) = \frac{150}{s}$

$\displaystyle (s^2 + 8s + 25) Q(s) = \frac{150}{s}$

$\displaystyle Q(s) = \frac{150}{s(s^2+8s+25)}$

$\displaystyle Q(s) = \frac{6}{s} - \frac{6s+48}{s^2+8s+25}$

$\displaystyle Q(s) = \frac{6}{s} - \frac{6(s+4-4)+48}{s^2+8s+16-16+25}$

$\displaystyle Q(s) = \frac{6}{s} - \frac{6(s+4)-24+48}{(s+4)^2-16+25}$

$\displaystyle Q(s) = \frac{6}{s} - \frac{6(s+4)+24}{(s+4)^2+9}$

$\displaystyle Q(s) = \frac{6}{s} - \frac{6(s+4)}{(s+4)^2+9} - \frac{24}{(s+4)^2+9}$

Aplicando la transformada inversa de Laplace en ambos lados

$\displaystyle \mathcal{L}^{-1} [Q(s)] = \mathcal{L}^{-1} \left[\frac{6}{s} - \frac{6(s+4)}{(s+4)^2+9} - \frac{24}{(s+4)^2+9} \right]$

$\displaystyle \mathcal{L}^{-1} [Q(s)] = 6 \ \mathcal{L}^{-1} \left[\frac{1}{s} \right] - 6 \ \mathcal{L}^{-1} \left[\frac{(s+4)}{(s+4)^2+9} \right] - 24 \ \mathcal{L}^{-1} \left[\frac{1}{(s+4)^2+9} \right]$

$\displaystyle q(t) = 6 - 6e^{-4t} \cos{3t} - \frac{24}{3} e^{-4t} \sin{3t}$

$\displaystyle q(t) = 6 - 6e^{-4t} \cos{3t} - 8 e^{-4t} \sin{3t}$

Derivando con respecto a $t$ ,

$\displaystyle \frac{dq}{dt} = \frac{d}{dt} \left[6 - 6e^{-4t} \cos{3t} - 8 e^{-4t} \sin{3t} \right]$

$\displaystyle \frac{dq}{dt} = \frac{d}{dt} [6] - 6 \frac{d}{dt} [e^{-4t} \cos{3t}] - 8 \frac{d}{dt} [e^{-4t} \sin{3t} ]$

$\displaystyle \frac{dq}{dt} = 0 - 6(-4 e^{-4t} \cos{3t} - 3 e^{-4t} \sin{3t}) - 8 (-4 e^{-4t} \sin{3t} + 3 e^{-4t} \cos{3t})$

$\displaystyle \frac{dq}{dt} = 24 e^{-4t} \cos{3t} + 18 e^{-4t} \sin{3t} + 32 e^{-4t} \sin{3t} - 24 e^{-4t} \cos{3t}$

$\displaystyle \frac{dq}{dt} = 50 e^{-4t} \sin{3t}$

Recordando que $\displaystyle \frac{dq}{dt}=i(t)$ ,

$\displaystyle i(t) = 50 e^{-4t} \sin{3t}$

Finalmente

$\displaystyle \begin{matrix} q(t) & = & 6 - 6e^{-4t} \cos{3t} - 8 e^{-4t} \sin{3t} \\ i(t) & = & 50 e^{-4t} \sin{3t} \end{matrix}$

Solución (b). Cuando $E=100 \sin{3t}$ voltios

$\displaystyle \frac{d^2 q}{{dt}^2} + 8 \frac{dq}{dt} + 25 q(t) - \frac{100 \sin{3t}}{2} = 0$

$\displaystyle \frac{d^2 q}{{dt}^2} + 8 \frac{dq}{dt} + 25 q(t) - 50 \sin{3t} = 0$

$\displaystyle \frac{d^2 q}{{dt}^2} + 8 \frac{dq}{dt} + 25 q(t) = 50 \sin{3t}$

Aplicando la transformada de Laplace en ambos miembros,

$\displaystyle \mathcal{L} \left[\frac{d^2 q}{{dt}^2} + 8 \frac{dq}{dt} + 25 q(t) \right] = \mathcal{L} [50 \sin{3t}]$

$\displaystyle \mathcal{L} \left[\frac{d^2 q}{{dt}^2} \right] + 8 \mathcal{L} \left[\frac{dq}{dt}\right] + 25 \mathcal{L} \left[q(t) \right] = 50 \ \mathcal{L} [\sin{3t}]$

$\displaystyle [s^2 Q(s) - s q(0) - q'(0)] + 8 [sQ(s) - q(0) ] + 25 Q(s) = \frac{150}{s^2+9}$

Continuando

$\displaystyle [s^2 Q(s) - s (0) - (0)] + 8 [sQ(s) - (0) ] + 25 Q(s) = \frac{150}{s^2+9}$

$\displaystyle s^2 Q(s) + 8s Q(s) + 25 Q(s) = \frac{150}{s^2+9}$

$\displaystyle (s^2 + 8s + 25) Q(s) = \frac{150}{s^2+9}$

$\displaystyle Q(s) = \frac{150}{(s^2+9)(s^2+8s+25)}$

$\displaystyle Q(s) = \frac{75}{26} \frac{1}{s^2+9} - \frac{75}{52} \frac{s}{s^2+9} + \frac{75}{26} \frac{(s+4)^2 + 9} + \frac{75}{52} \frac{s+4}{(s+4)^2 + 9}$

Aplicando la transformada inversa de Laplace en ambos lados

$\displaystyle \mathcal{L}^{-1} [Q(s)] = \mathcal{L}^{-1} \left[\frac{75}{26} \frac{1}{s^2+9} - \frac{75}{52} \frac{s}{s^2+9} + \frac{75}{26} \frac{1}{(s+4)^2 + 9} + \frac{75}{52} \frac{s+4}{(s+4)^2 + 9} \right]$

$\displaystyle \mathcal{L}^{-1} [Q(s)] = \frac{75}{26} \ \mathcal{L}^{-1} \left[\frac{1}{s^2+9} \right] - \frac{75}{52} \mathcal{L}^{-1} \left[\frac{s}{s^2+9} \right] + \frac{75}{26} \mathcal{L}^{-1} \left[\frac{1}{(s+4)^2 + 9} \right] + \frac{75}{52} \mathcal{L}^{-1} \left[\frac{s+4}{(s+4)^2 + 9} \right]$

$\displaystyle q(t) = \frac{25}{26} \sin{3t} - \frac{75}{52} \cos{3t} + \frac{25}{26} e^{-4t} \sin{3t} + \frac{75}{52} e^{-4t} \cos{3t}$

$\displaystyle q(t) = \frac{25}{52} (2 \sin{3t} - 3 \cos{3t}) + \frac{25}{52} e^{-4t} (2 \sin{3t} + 3 \cos{3t})$

Derivando con respecto a $t$ ,

$\displaystyle \frac{dq}{dt} = \frac{d}{dt} \left[\frac{25}{52} (2 \sin{3t} - 3 \cos{3t}) + \frac{25}{52} e^{-4t} (2 \sin{3t} + 3 \cos{3t}) \right]$

$\displaystyle \frac{dq}{dt} = \frac{25}{52} \frac{d}{dt} (2 \sin{3t} - 3 \cos{3t}) + \frac{25}{52} \frac{d}{dt} \left[e^{-4t} (2 \sin{3t} + 3 \cos{3t}) \right]$

$\displaystyle \frac{dq}{dt} = \frac{75}{52} (2 \cos{3t} + 3 \sin{3t}) - \frac{25}{52} e^{-4t} (17 \sin{3t} + 6 \cos{3t})$

Recordando que $\displaystyle \frac{dq}{dt} = i(t)$ ,

$\displaystyle i(t) = \frac{75}{52} (2 \cos{3t} + 3 \sin{3t}) - \frac{25}{52} e^{-4t} (17 \sin{3t} + 6 \cos{3t})$

Finalmente,

$\displaystyle \begin{matrix} q(t) & = & \frac{25}{52} (2 \sin{3t} - 3 \cos{3t}) + \frac{25}{52} e^{-4t} (2 \sin{3t} + 3 \cos{3t}) \\ i(t) & = & \frac{75}{52} (2 \cos{3t} + 3 \sin{3t}) - \frac{25}{52} e^{-4t} (17 \sin{3t} + 6 \cos{3t}) \end{matrix}$

Problema 2. Dada la malla eléctrica de la figura siguiente, determinar las corrientes de las diferentes ramas, si las corrientes iniciales valen cero.

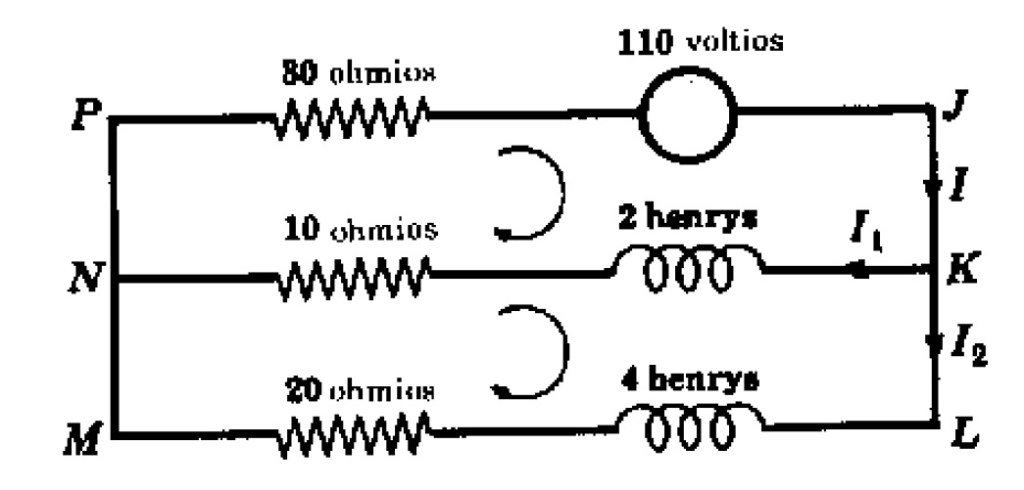
Solución. Las mallas KLMNK y JKNPJ se recorren en el sentido de las agujas del reloj. Al recorrer estas mallas se deben considerar positivas las caídas de voltaje, cuando el recorrido es un sentido opuesto al de la corriente. Una subida del voltaje se considera como una caída de voltaje con signo opuesto.

Sea $i$ la corriente en el recorrido NPJK. En el nodo K esta corriente se divide $i_1$ e $i_2$ en tal forma que $i = i_1 + i_2$ .

En la malla KLMNK la ley de Kirchhoff para los voltajes, se tiene que

$\displaystyle \sum{v_k} = 0$

$\displaystyle - R_2 i_1 - L_1 \frac{di_1}{dt} + L_2 \frac{di_2}{dt} + R_3 i_2 = 0$

$\displaystyle - 10 i_1 - 2 \frac{di_1}{dt} + 4 \frac{di_2}{dt} + 20 i_2 = 0$

$\displaystyle - 2 \frac{di_1}{dt} + 4 \frac{di_2}{dt} -10 i_1 + 20 i_2 = 0$

$\displaystyle \frac{di_1}{dt} - 2 \frac{di_2}{dt} + 5 i_1 - 10 i_2 = 0$

Aplicando la transformada de Laplace

$\displaystyle \mathcal{L} \left[\frac{di_1}{dt} - 2 \frac{di_2}{dt} + 5 i_1 - 10 i_2 \right] = \mathcal{L} [0]$

$\displaystyle \mathcal{L} \left[\frac{di_1}{dt}\right] - 2 \mathcal{L} \left[\frac{di_2}{dt} \right] + 5 \mathcal{L} [i_1] - 10 \mathcal{L} [i_2] = \mathcal{L} [0]$

$\displaystyle s I_1 (s) - i_1 (0) - 2 [s I_2 (s) - i_2 (0)] + 5 I_1 (s) - 10 I_2 (s) = 0$

$\displaystyle s I_1 (s) - 0 - 2s I_2 (s) + 5 I_1 (s) - 10 I_2 (s) = 0$

$\displaystyle (s+5) I_1 (s) - (2s + 10) I_2 (s) = 0$

$\displaystyle (s+5) I_1 (s) = (2s + 10) I_2 (s)$

$\displaystyle (s+5) I_1 (s) = 2(s + 5) I_2 (s)$

$\displaystyle I_1 (s) = 2 I_2 (s)$

Utilizando la transformada inversa de Laplace,

$\displaystyle \mathcal{L}^{-1} [I_1 (s)] = 2 \mathcal{L}^{-1} [I_2 (s)]$

$\displaystyle i_1 (t) = 2 i_2 (t)$

Y para la malla JKNPJ,

$\displaystyle \sum{v_k} = 0$

$\displaystyle R_1 i - E + L_1 \frac{di_1}{dt} + R_2 i_1 = 0$

$\displaystyle R_1 i_1 + R_1 i_2 - E + L_1 \frac{di_1}{dt} + R_2 i_1 = 0$

$\displaystyle 30 i_1 + 30 i_2 - 110 + 2 \frac{di_1}{dt} + 10 i_1 = 0$

$\displaystyle 2 \frac{di_1}{dt} + 40 i_1 + 30 I_2 = 110$

$\displaystyle \frac{di_1}{dt} + 20 i_1 + 15 I_2 = 55$

Aplicando la transformada de Laplace

$\displaystyle \mathcal{L} \left[ \frac{di_1}{dt} + 20 i_1 + 15 I_2 \right] = \mathcal{L} [55]$

$\displaystyle \mathcal{L} \left[ \frac{di_1}{dt} \right] + 20 \mathcal{L} [i_1] + 15 \mathcal{L} [I_2] = \mathcal{L} [55]$

$\displaystyle s I_1 (s) - i_1 (0) + 20 I_1 (s) + 15 I_2 (s)] = \frac{55}{s}$

$\displaystyle s I_1 (s) - 0 + 20 I_1 (s) + 15 I_2 (s)] = \frac{55}{s}$

$\displaystyle (s + 20) I_1 (s) + 15 I_2 (s) = \frac{55}{s}$

Recordando que $I_1 (s) = 2 I_2 (s)$ , resulta que

$\displaystyle (s + 20)[2 I_2 (s)] + 15 I_2 (s) = \frac{55}{s}$

$\displaystyle (2s + 40) I_2 (s) + 15 I_2 (s) = \frac{55}{s}$

$\displaystyle (2s + 55) I_2 (s) = \frac{55}{s}$

$\displaystyle I_2 (s) = \frac{55}{s(2s+55)}$

$\displaystyle I_2 (s) = \frac{1}{s} - \frac{2}{2s+55}$

Aplicando la transformada inversa de Laplace,

$\displaystyle \mathcal{L}^{-1} [I_2 (s)] = \mathcal{L}^{-1} \left[\frac{1}{s} - \frac{2}{2s+55} \right]$

$\displaystyle \mathcal{L}^{-1} [I_2 (s)] = \mathcal{L}^{-1} \left[\frac{1}{s} \right] - 2\ \mathcal{L}^{-1} \left[\frac{1}{2s+55} \right]$

$\displaystyle i_2 (t) = 1 - e^{-55t/2}$

Sustituyendo en el resultado de $i_1 (t)$

$\displaystyle i_1 (t) = 2 i_2 (t)$

$\displaystyle i_1 (t) = 2 (1 - e^{-55t/2})$

$\displaystyle i_1 (t) = 2 - 2 e^{-55t/2}$

Y en la ecuación $i$

$\displaystyle i = 1 - e^{-55t/2} + 2 - 2 e^{-55t/2}$

$\displaystyle i = 3 - 3 e^{-55t/2}$

Finalmente

$\displaystyle \begin{matrix} i (t) & = & 3 - 3 e^{-55t/2} \\ i_1 (t) & = & 2 - 2 e^{-55t/2} \\ i_2 (t) & = & 1 - e^{-55t/2} \end{matrix}$

Aplicaciones a circuitos eléctricos y la transformada de Laplace. Laplace.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Aplicaciones a circuitos eléctricos y la transformada de Laplace. Laplace.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta