Aplicaciones a las vigas y la transformada de Laplace. Laplace.

Introducción

Suponiendo que una viga cuyos extremos están en $x=0$ y $x=l$ coincide con el eje $x$ y tiene una carga vertical $W(x)$ por unidad de longitud que actúa transversalmente sobre la viga. Entonces el eje de la viga tiene una deflexión transversal $y(x)$ en el punto $x$ , la cual satisface la ecuación diferencial

$\displaystyle \frac{d^4y}{dx^4} = \frac{W(x)}{EI}$ donde $0<x<l$

Esta deflexión transversal se llama a veces la curva de deflexión o curva elástica. La cantidad $EI$ se llama rigidez de la flexión de la viga y es constante (por suposición); por lo regular, $E$ es el módulo de elasticidad de Young para esta viga y $I$ es el momento de inercia de una sección recta de la viga con relación al eje. Las cantidades $EIy''(x)$ y $EI y'''(x)$ se llaman, respectivamente, el momento flector y el esfuerzo secante en x. Nótese que en el eje $y$ se elige como positivo el sentido hacia abajo, de tal manera que las deflexiones son positivas hacia abajo.

Figura 3.4.1 — *Figura 1. Representación de una viga que contiene una carga.*

Las condiciones de la frontera asociadas a la ecuación diferencial dependen de la manera como esté apoyada la viga. Las más comunes son:

Empotrada: $y(0) = 0$ , $y'(0) = 0$
Articulada: $y(0) = 0$ , $y''(0) = 0$
Apoyo simple: $y''(0) = 0$ , $y'''(0) = 0$

Problemas resueltos

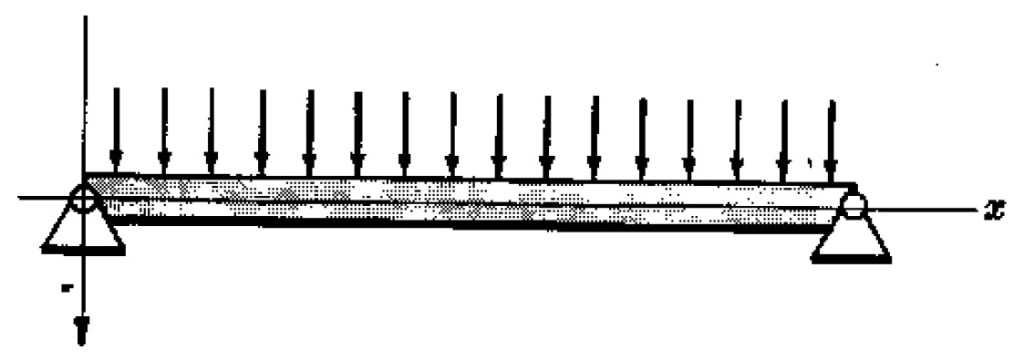
Problema 1. Una viga fija en sus extremos $x=0$ y $x=l$ soporta una carga uniforme $W_0$ por unidad de longitud. Hallar la deflexión en cualquier punto.

Solución. Tomando la ecuación diferencial

$\displaystyle \frac{d^4y}{dx^4} = \frac{W_0}{EI}$ $0<x<l$

y sus condiciones de frontera: $\displaystyle y(0) = 0$ , $\displaystyle y''(0) = 0$ , $y(l)=0$ , $y''(l) = 0$ .

Aplicando la transformada de Laplace en ambos miembros,

$\displaystyle \mathcal{L} \left[\frac{d^4y}{dx^4} \right] = \mathcal{L} \left[\frac{W_0}{EI} \right]$

$\displaystyle s^4 Y(s) - s^3 y(0) - s^2 y'(0) - s y''(0) - y'''(0) = \frac{W_0}{EI} \frac{1}{s}$

Sustituyendo en la condiciones iniciales

$\displaystyle s^4 Y(s) - s^2 y'(0) - y'''(0) = \frac{W_0}{EI} \frac{1}{s}$

Ahora, sea $y'(0) = c_1$ y $y'''(0) = c_2$ (debido a que se desconocen estas condiciones)

$\displaystyle s^4 Y(s) - s^2 \cdot c_1 - c_2 = \frac{W_0}{EI} \frac{1}{s}$

$\displaystyle s^4 Y(s) - c_1 s^2 - c_2 = \frac{W_0}{EI} \frac{1}{s}$

Despejando $Y(s)$ ,

$\displaystyle s^4 Y(s) = c_1 s^2 + c_2 + \frac{W_0}{EI} \frac{1}{s}$

$\displaystyle Y(s) = \frac{c_1}{s^2} + \frac{c_2}{s^4} + \frac{W_0}{EI} \frac{1}{s^5}$

Aplicando la transformada inversa de Laplace en ambos lados,

$\displaystyle \mathcal{L}^{-1} [Y(s)] = \mathcal{L}^{-1} \left[ \frac{c_1}{s^2} + \frac{c_2}{s^4} + \frac{W_0}{EI} \frac{1}{s^5} \right]$

$\displaystyle \mathcal{L}^{-1} [Y(s)] = c_1 \ \mathcal{L}^{-1} \left[ \frac{1}{s^2} \right] + c_2 \ \mathcal{L}^{-1} \left[\frac{1}{s^4} \right] + \frac{W_0}{EI} \ \mathcal{L} \left[\frac{1}{s^5} \right]$

$\displaystyle y(x) = c_1 x + c_2 \ \frac{x^3}{3!} + \frac{W_0}{EI} \ \frac{x^4}{4!}$

$\displaystyle y(x) = c_1 x + \frac{c_2}{6} x^3 + \frac{W_0}{24EI} x^4$

Se determinan los valores de $c_1$ y $c_2$ tomando el resultado de $y(x)$ y determinando su segunda derivada.

$\displaystyle y'(x) = c_1 + \frac{c_2}{2} x^2 + \frac{W_0}{6EI} x^3$

$\displaystyle y''(x) = c_2 x + \frac{W_0}{2EI} x^2$

De la función $y(x)$ , se toma la condición $y(l) = 0$ .

$\displaystyle y(l) = c_1 l + \frac{c_2}{6} l^3 + \frac{W_0}{24EI} l^4$

$\displaystyle 0 = c_1 l + \frac{c_2}{6} l^3 + \frac{W_0}{24EI} l^4$

$\displaystyle c_1 l + \frac{c_2}{6} l^3 = - \frac{W_0}{24EI} l^4$

$\displaystyle c_1 + \frac{c_2}{6} l^2 = - \frac{W_0}{24EI} l^3$

Y del resultado de $y''(x)$ , se toma la condición $y''(l) = 0$ .

$\displaystyle y''(l) = c_2 l + \frac{W_0}{2EI} l^2$

$\displaystyle 0 = c_2 l + \frac{W_0}{2EI} l^2$

$\displaystyle c_2 l + \frac{W_0}{2EI} l^2 = 0$

Teniendo las ecuaciones,

\displaystyle c_1 + \frac{c_2}{6} l^2 = - \frac{W_0}{24EI} l^3

\displaystyle c_2 l + \frac{W_0}{2EI} l^2 = 0

Resolviendo este sistema, los valores son $\displaystyle c_1 = \frac{W_0 l^3}{24 EI}$ y $\displaystyle c_2 = - \frac{W_0 l}{2 EI}$ . Sustituyendo estos valores en la función $y(x)$ , el resultado final es

$\displaystyle y(x) = c_1 x + \frac{c_2}{6} x^3 + \frac{W_0}{24EI} x^4$

$\displaystyle y(x) = \frac{W_0 l^3}{24 EI} x - \frac{W_0 l}{12 EI} x^3 + \frac{W_0}{24EI} x^4$

$\displaystyle \therefore y(x) = \frac{W_0}{24 EI} (x^4 - 2 l x^3 + l^3 x)$

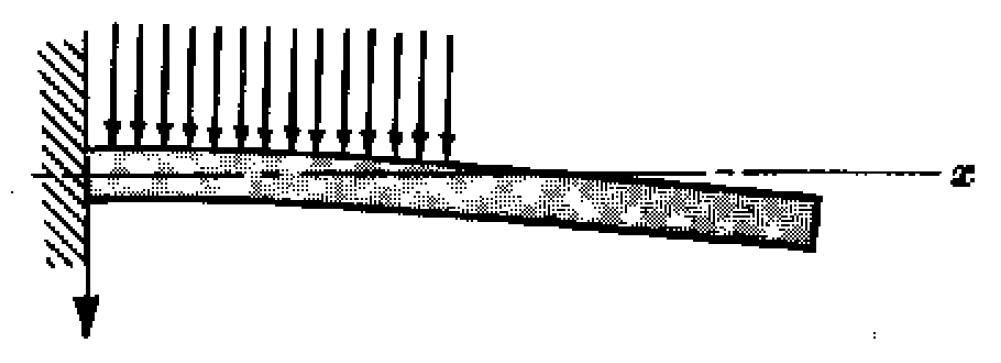
Problema 2. Una viga voladiza (viga cantilever) asegurada en el extremo $x=0$ y libre en el extremo $x=l$ , soporta una carga $W(x)$ por unidad de longitud dada por

$\displaystyle W(x) = \left\{ \begin{matrix} W_0 & 0 < x < \frac{l}{2} \\ 0 & \frac{l}{2} < x < l \end{matrix} \right.$

Hallar su deflexión.

Solución. Tomando la ecuación diferencial,

$\displaystyle \frac{d^4y}{dx^4} = \frac{W(x)}{EI}$

y sus condiciones son $y(0)=0$ , $y'(0) =0$ , $y''(l)=0$ y $y'''(l)=0$ . Además, la función $W(x)$ puede expresarse en términos de la función unitaria de Heaviside

$\displaystyle W(x) = W_0 \left[U(x) - U \left(x-\frac{l}{2} \right) \right]$

Entonces, determinando la transformada de Laplace en ambos miembros de la ecuación diferencial

$\displaystyle \frac{d^4y}{dx^4} = \frac{W(x)}{EI}$

$\displaystyle \frac{d^4y}{dx^4} = \frac{W_0}{EI} \left[U(x) - U \left(x-\frac{l}{2} \right) \right]$

$\displaystyle \mathcal{L} \left[\frac{d^4y}{dx^4} \right] = \frac{W_0}{EI} \mathcal{L} \left[U(x) - U \left(x-\frac{l}{2} \right) \right]$

$\displaystyle \mathcal{L} \left[\frac{d^4y}{dx^4} \right] = \frac{W_0}{EI} \mathcal{L} \left[U(x) \right] - \mathcal{L} \left[U \left(x-\frac{l}{2} \right) \right]$

$\displaystyle s^4 Y(s) - s^3 y(0) - s^2 y'(0) - s y''(0) - y'''(0) = \frac{W_0}{EI} \left( \frac{1}{s} -\frac{e^{-sl/2}}{s} \right)$

Aplicando las condiciones dadas, resulta que,

$\displaystyle s^4 Y(s) - s y''(0) - y'''(0) = \frac{W_0}{EI} \left( \frac{1}{s} -\frac{e^{-sl/2}}{s} \right)$

Asignando a $y''(0)=c_1$ y $y'''(0)=c_2$ debido a que no existen condiciones

$\displaystyle s^4 Y(s) - c_2 s - c_3 = \frac{W_0}{EI} \left( \frac{1}{s} -\frac{e^{-sl/2}}{s} \right)$

Despejando $Y(s)$

$\displaystyle s^4 Y(s) = c_2 s + c_3 + \frac{W_0}{EI} \left( \frac{1}{s} -\frac{e^{-sl/2}}{s} \right)$

$\displaystyle Y(s) = \frac{c_2}{s^3} + \frac{c_3}{s^4} + \frac{W_0}{EI} \left( \frac{1}{s^5} -\frac{e^{-sl/2}}{s^5} \right)$

Determinando su transformada inversa,

$\displaystyle \mathcal{L}^{-1} [Y(s)] = \mathcal{L}^{-1} \left[\frac{c_2}{s^3} + \frac{c_3}{s^4} + \frac{W_0}{EI} \left( \frac{1}{s^5} -\frac{e^{-sl/2}}{s^5} \right) \right]$

$\displaystyle \mathcal{L}^{-1} [Y(s)] = c_2 \mathcal{L}^{-1} \left[\frac{1}{s^3} \right] + c_3 \mathcal{L}^{-1} \left[\frac{1}{s^4} \right] + \frac{W_0}{EI} \mathcal{L}^{-1} \left[\left( \frac{1}{s^5} -\frac{e^{-sl/2}}{s^5} \right) \right]$

$\displaystyle y(x) = \frac{c_1}{2!} x^2 + \frac{c_2}{3!} x^3 + \frac{W_0}{EI} \frac{1}{4!} \left[ x^4 - \left(x - \frac{l}{2} \right)^4 U \left(x - \frac{l}{2} \right) \right]$

$\displaystyle y(x) = \frac{c_1}{2} x^2 + \frac{c_2}{6} x^3 + \frac{W_0}{24EI} \left[ x^4 - \left(x - \frac{l}{2} \right)^4 U \left(x - \frac{l}{2} \right) \right]$

$\displaystyle y(x) = \frac{c_1}{2} x^2 + \frac{c_2}{6} x^3 + \frac{W_0}{24EI} x^4 - \frac{W_0}{24EI} \left(x - \frac{l}{2} \right)^4 U \left(x - \frac{l}{2} \right)$

Cuyo resultado también es,

$\displaystyle y(x) = \left\{\begin{matrix} \frac{c_1}{2} x^2 + \frac{c_2}{6} x^3 + \frac{W_0}{24EI} x^4 & 0 < x < \frac{l}{2} \\ \frac{c_1}{2} x^2 + \frac{c_2}{6} x^3 + \frac{W_0}{24EI} x^4 - \frac{W_0}{24EI} \left(x - \frac{l}{2} \right)^4 & x > \frac{l}{2} \end{matrix} \right.$

Las constantes $c_1$ y $c_2$ son

$\displaystyle c_1 = \frac{W_0 l^2}{8EI}$ y $\displaystyle c_2 = - \frac{W_0 l}{2EI}$

Entonces,

$\displaystyle y(x) = \frac{W_0 l^2}{16EI} x^2 - \frac{W_0 l}{12EI} x^3 + \frac{W_0}{24EI} x^4 - \frac{W_0}{24EI} \left(x - \frac{l}{2} \right)^4 U \left(x - \frac{l}{2} \right)$

Finalmente, la función esperada es

$\displaystyle \therefore y(x) = \frac{W_0 l^2}{16EI} x^2 - \frac{W_0 l}{12EI} x^3 + \frac{W_0}{24EI} x^4 - \frac{W_0}{24EI} \left(x - \frac{l}{2} \right)^4 U \left(x - \frac{l}{2} \right)$

O también,

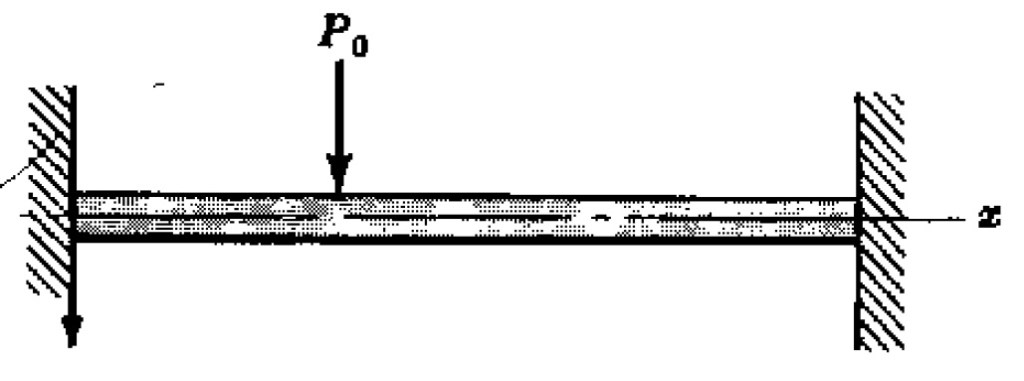
$\displaystyle \therefore y(x) = \left\{\begin{matrix} \frac{W_0 l^2}{16EI} x^2 - \frac{W_0 l}{12EI} x^3 + \frac{W_0}{24EI} x^4 & 0<x<\frac{l}{2} \\ \frac{W_0 l^2}{16EI} x^2 - \frac{W_0 l}{12EI} x^3 + \frac{W_0}{24EI} x^4 - \frac{W_0}{24EI} \left(x - \frac{l}{2} \right)^4 & \frac{l}{2} <x<l \end{matrix} \right.$

Problema 3. Una viga tiene empotrados sus extremos en $x=0$ y $x=l$ . En el punto $x=l/3$ actúa, verticalmente hacia abajo, una carga concentrada $P_0$ . Hallar la deflexión resultante.

*Figura 4. Viga empotrada en sus extremos con una carga concentrada hacia abajo.*

Solución. Considerando una carga uniforme $P_0$ por unidad de longitud sobre la parte de la viga comprendida entre $\displaystyle \frac{l}{3}$ y $\displaystyle \frac{l}{3} + \epsilon$ . Entonces la carga total sobre esta parte de la viga es

$P_0 \left(\frac{l}{3} + \epsilon - \frac{l}{3} \right) = P_0 \epsilon$

Como esta carga total es igual a $P_0$ , se tiene que

$\displaystyle W(x) = \left\{\begin{matrix} \frac{P_0}{\epsilon} & \frac{l}{3}<x<\frac{l}{3} + \epsilon \\ 0 & \text{en cualquier otra parte} \end{matrix} \right.$

Pero al establecer el límite cuando $\epsilon \rightarrow 0$ , se establece que

$\displaystyle W(x) = P_0 \ \delta \left(x-\frac{l}{3} \right)$

donde $\delta$ es la función delta de Dirac o función impulso. Entonces, la ecuación diferencial de la deflexión es

$\displaystyle \frac{d^4 y}{{dx}^4} = \frac{P_0}{EI} \delta \left(x - \frac{l}{3} \right)$

cuyas condiciones de frontera son $y(0) = 0$ , $y'(0) =0$ , $y(l)=0$ , $y'(l)=0$ . Aplicando la transformada de Laplace en ambos miembros, resulta lo siguiente,

$\displaystyle \mathcal{L} \left[\frac{d^4 y}{{dx}^4} \right] = \frac{P_0}{EI} \mathcal{L} \left[[ \delta \left(x - \frac{l}{3} \right) \right]$

$\displaystyle s^4 Y(s) - s^3 y(0) - s^2 y'(0) - s y''(0) - y'''(0) = \frac{P_0}{EI} e^{-ls/3}$

Recordando los valores de frontera y sustituyendo $y''(0)=c_1$ y $y'''(0)=c_3$ debido a que se desconocen sus valores, se tiene que

$\displaystyle s^4 Y(s) - c_1 s - c_2 = \frac{P_0}{EI} e^{-ls/3}$

Despejando $Y(s)$

$\displaystyle s^4 Y(s) = c_1 s + c_2 + \frac{P_0}{EI} e^{-ls/3}$

$\displaystyle Y(s) = \frac{c_1}{s^3} + \frac{c_2 }{s^4}+ \frac{P_0}{EI} \frac{e^{-ls/3}}{s^4}$

Aplicando la transformada inversa de Laplace en ambos lados, resulta que

$\displaystyle \mathcal{L}^{-1} [Y(s)] = \mathcal{L}^{-1} \left[\frac{c_1}{s^3} + \frac{c_2 }{s^4}+ \frac{P_0}{EI} \frac{e^{-ls/3}}{s^4} \right]$

$\displaystyle \mathcal{L}^{-1} [Y(s)] = c_1 \ \mathcal{L}^{-1} \left[\frac{1}{s^3} \right] + c_2 \ \mathcal{L}^{-1} \left[\frac{1}{s^4} \right] + \frac{P_0}{EI} \ \mathcal{L}^{-1} \left[\frac{e^{-ls/3}}{s^4} \right]$

$\displaystyle y(x) = \frac{c_1}{2!} x^2 + \frac{c_2}{3!} x^3 + \frac{P_0}{EI} \ \frac{(x - l/3)^3}{3!} U \left(x - \frac{l}{3} \right)$

$\displaystyle y(x) = \frac{c_1}{2} x^2 + \frac{c_2}{6} x^3 + \frac{P_0}{6EI} \left(x - \frac{l}{3} \right)^3 U \left(x - \frac{l}{3} \right)$

Cuyo resultado también es

$\displaystyle y(x) = \left\{\begin{matrix} \frac{c_1}{2} x^2 + \frac{c_2}{6} x^3 & 0<x<\frac{l}{3} \\ \frac{c_1}{2} x^2 + \frac{c_2}{6} x^3 + \frac{P_0}{6EI} \left(x - \frac{l}{3} \right)^3 & \frac{l}{3} <x<l \end{matrix} \right.$

Las constantes $c_1$ y $c_2$ son

$\displaystyle c_1 = \frac{4 P_0 l}{27 EI}$ y $\displaystyle c_2 = - \frac{20 P_0}{27 EI}$

Sustituyendo estos valores en el resultado de $y(x)$ , el resultado final es

$\displaystyle \therefore y(x) = \frac{2 P_0 l}{27 EI} x^2 - \frac{10}{81 EI} x^3 + \frac{P_0}{6EI} \left(x - \frac{l}{3} \right)^3 U \left(x - \frac{l}{3} \right)$

O también,

$\displaystyle \therefore y(x) = \left\{\begin{matrix} \frac{2 P_0 l}{27 EI} x^2 - \frac{10}{81 EI} x^3 & 0 < x < \frac{l}{3} \\ \frac{2 P_0 l}{27 EI} x^2 - \frac{10}{81 EI} x^3 & \frac{l}{3} < x < l \end{matrix} \right.$

Aplicaciones a las vigas y la transformada de Laplace. Laplace.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Aplicaciones a las vigas y la transformada de Laplace. Laplace.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta