Utilización del teorema del residuo para hallar la transformada inversa de Laplace de una función. Laplace.

Introducción

Suponiendo que las únicas singularidades de $F(s)$ son polos, todos ellos a la izquierda de la recta $s=\gamma$ , para alguna constante real $\gamma$ . Suponiendo además que la integral expresada en la ecuación

$\displaystyle f(t) = \frac{1}{2\pi i} \oint_{C}{e^{st} \ F(s) \, ds} = \lim_{R \rightarrow \infty}{\frac{1}{2\pi i} \int_{\gamma - iT}^{\gamma + iT}{e^{st} \ F(s) \, ds}}$

a lo largo de $\Gamma$ tiende a cero cuando $R \rightarrow \infty$ . Entonces, por el teorema del residuo, la ecuación anterior toma la forma

$\displaystyle f(t) =$ suma de residuos de $e^{st} \ F(s)$ en los polos de $F(s)$

$\displaystyle f(t) = \sum{}$ residuos de $e^{st} \ F(s)$ en los polos de $F(s)$

Demostración

Se empieza por suponer que las únicas singularidades de $F(s)$ son polos situados todos ellos a la izquierda de la recta $s = \gamma$ para alguna constante real $\gamma$ . Ahora,

$\displaystyle \frac{1}{2\pi i} \oint_C{e^{st} \ F(s) \ ds} = \frac{1}{2\pi i} \int_{\gamma - iT}^{\gamma + iT}{e^{st} \ F(s) \ ds} + \frac{1}{2\pi i}\int_{\Gamma}{e^{st} \ F(s) \ ds}$

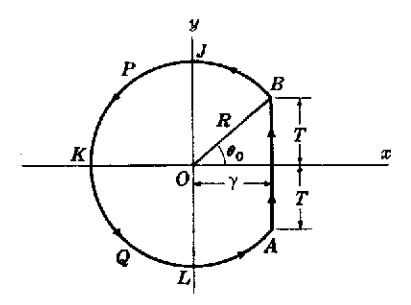
donde $C$ es el contorno de Bromwich y $\Gamma$ es el arco circular $BJPKQLA$ mostrado en la figura 1.

Por el teorema del residuo,

$\displaystyle \frac{1}{2\pi i} \oint_{C}{e^{st} \ F(s) \ ds} = \text{suma de los residuos de } e^{st} \ F(s) \text{ en todos los polos dentro de } C$

$\displaystyle \frac{1}{2\pi i} \oint_{C}{e^{st} \ F(s) \ ds} = \sum{\text{residuos dentro de } C}$

Así,

$\displaystyle \frac{1}{2\pi i} \oint_C{e^{st} \ F(s) \ ds} = \frac{1}{2\pi i} \int_{\gamma - iT}^{\gamma + iT}{e^{st} \ F(s) \ ds} + \frac{1}{2\pi i}\int_{\Gamma}{e^{st} \ F(s) \ ds}$

$\displaystyle \sum{\text{residuos dentro de } C} = \frac{1}{2\pi i} \int_{\gamma - iT}^{\gamma + iT}{e^{st} \ F(s) \ ds} + \frac{1}{2\pi i}\int_{\Gamma}{e^{st} \ F(s) \ ds}$

$\displaystyle \sum{\text{residuos dentro de } C} - \frac{1}{2\pi i}\int_{\Gamma}{e^{st} \ F(s) \ ds} = \frac{1}{2\pi i} \int_{\gamma - iT}^{\gamma + iT}{e^{st} \ F(s) \ ds}$

$\displaystyle \frac{1}{2\pi i} \int_{\gamma - iT}^{\gamma + iT}{e^{st} \ F(s) \ ds} = \sum{\text{residuos dentro de } C} - \frac{1}{2\pi i} \int_{\Gamma}{e^{st} \ F(s) \ ds}$

Tomando el límite cuando $R \rightarrow \infty$ ,

$\displaystyle \lim_{R \rightarrow \infty}{\frac{1}{2\pi i} \int_{\gamma - iT}^{\gamma + iT}{e^{st} \ F(s) \ ds}} = \lim_{R \rightarrow \infty}{\left[\sum{\text{residuos dentro de } C} - \frac{1}{2\pi i} \int_{\Gamma}{e^{st} \ F(s) \ ds} \right]}$

$\displaystyle \lim_{R \rightarrow \infty}{\frac{1}{2\pi i} \int_{\gamma - iT}^{\gamma + iT}{e^{st} \ F(s) \ ds}} = \lim_{R \rightarrow \infty}{\sum{\text{residuos dentro de } C}} - \lim_{R \rightarrow \infty}{\frac{1}{2\pi i} \int_{\Gamma}{e^{st} \ F(s) \ ds}}$

$\displaystyle f(t) = \sum{\text{residuos dentro de } C} - \frac{1}{2\pi i} (0)$

$\displaystyle \therefore f(t) = \sum{\text{residuos dentro de } C}$

Problemas resueltos

Problema 1. Calcular $\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s-2)} \right]$ .

Solución. Se tiene lo siguiente,

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s-2)} \right] = \frac{1}{2\pi i} \int_{\gamma - i \infty}^{\gamma + i \infty}{\frac{e^{st}}{(s-2)} \ ds}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s-2)} \right] = \frac{1}{2\pi i} \oint_{C}{\frac{e^{st}}{(s-2)} \ ds}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s-2)} \right] = \sum{\text{residuos de } \frac{e^{st}}{(s-2)} \text{ en el polo } s=2}$

El residuo en el polo simple $s=2$ es

$\displaystyle \lim_{s \rightarrow 2}{(s-2) \cdot \frac{e^{st}}{(s-2)}} = \lim_{s \rightarrow 2}{e^{st}}$

$\displaystyle \lim_{s \rightarrow 2}{(s-2) \cdot \frac{e^{st}}{(s-2)}} = e^{2t}$

Regresando

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s-2)} \right] = \sum{\text{residuos de } \frac{e^{st}}{(s-2)} \text{ en el polo } s=2}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s-2)} \right] = e^{2t}$

Finalmente,

$\displaystyle \therefore \mathcal{L}^{-1} \left[\frac{1}{(s-2)} \right] = e^{2t}$

Problema 2. Calcular $\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s+1)(s-2)^2} \right]$ .

Solución. Se tiene lo siguiente

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s+1)(s-2)^2} \right] = \frac{1}{2\pi i} \int_{\gamma - i \infty}^{\gamma + i \infty}{\frac{e^{st}}{(s+1)(s-2)^2} \ ds}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s+1)(s-2)^2} \right] = \frac{1}{2\pi i} \oint_{C}{\frac{e^{st}}{(s+1)(s-2)^2} \ ds}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s+1)(s-2)^2} \right] = \sum{\text{residuos de } \frac{e^{st}}{(s+1)(s-2)^2} \text{ en los polos } s=-1 \ \text{y} \ s=2}$

El residuo en el polo $s=-1$ es

$\displaystyle \lim_{s \rightarrow -1}{\left[(s+1) \cdot \frac{e^{st}}{(s+1)(s-2)^2} \right]} = \lim_{s \rightarrow -1}{\frac{e^{st}}{(s-2)^2}}$

$\displaystyle \lim_{s \rightarrow -1}{\left[(s+1) \cdot \frac{e^{st}}{(s+1)(s-2)^2} \right]} = \frac{e^{(-1)t}}{(-1-2)^2} = \frac{e^{-t}}{(-3)^2} = \frac{e^{-t}}{9}$

$\displaystyle \lim_{s \rightarrow -1}{\left[(s+1) \cdot \frac{e^{st}}{(s+1)(s-2)^2} \right]} = \frac{1}{9} e^{-t}$

Y el residuo en el polo doble $s=2$ es

$\displaystyle \lim_{s \rightarrow 2}{\frac{1}{1!} \frac{d}{ds} \left[(s-2)^2 \cdot \frac{e^{st}}{(s+1)(s-2)^2} \right]} = \lim_{s \rightarrow -1}{\frac{1}{1} \frac{d}{ds} \left[\frac{e^{st}}{(s+1)} \right]}$

$\displaystyle \lim_{s \rightarrow 2}{\frac{1}{1!} \frac{d}{ds} \left[(s-2)^2 \cdot \frac{e^{st}}{(s+1)(s-2)^2} \right]} = \lim_{s \rightarrow -1}{\left[\frac{t(s+1) e^{st} - e^{st}}{(s+1)^2} \right]}$

$\displaystyle \lim_{s \rightarrow 2}{\frac{1}{1!} \frac{d}{ds} \left[(s-2)^2 \cdot \frac{e^{st}}{(s+1)(s-2)^2} \right]} = \frac{t(2+1) e^{2t} - e^{2t}}{(2+1)^2} = \frac{3te^{2t} - e^{2t}}{3^2}$

$\displaystyle \lim_{s \rightarrow 2}{\frac{1}{1!} \frac{d}{ds} \left[(s-2)^2 \cdot \frac{e^{st}}{(s+1)(s-2)^2} \right]} = \frac{3te^{2t} - e^{2t}}{9} = \frac{3}{9} te^{2t} - \frac{1}{9} e^{2t}$

$\displaystyle \lim_{s \rightarrow 2}{\frac{1}{1!} \frac{d}{ds} \left[(s-2)^2 \cdot \frac{e^{st}}{(s+1)(s-2)^2} \right]} = \frac{1}{3} te^{2t} - \frac{1}{9} e^{2t}$

Regresando

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s+1)(s-2)^2} \right] = \sum{\text{residuos de } \frac{e^{st}}{(s+1)(s-2)^2} \text{ en los polos } s=-1 \ \text{y} \ s=2}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s+1)(s-2)^2} \right] = \frac{1}{9} e^{-t} + \frac{1}{3} te^{2t} - \frac{1}{9} e^{2t}$

Finalmente

$\displaystyle \therefore \mathcal{L}^{-1} \left[\frac{1}{(s+1)(s-2)^2} \right] = \frac{1}{9} e^{-t} + \frac{1}{3} te^{2t} - \frac{1}{9} e^{2t}$

Problema 3. Calcular $\displaystyle \mathcal{L}^{-1} \left[\frac{s}{(s+1)^3 (s-1)^2} \right]$ .

Solución. Se tiene lo siguiente,

$\displaystyle \mathcal{L}^{-1} \left[\frac{s}{(s+1)^3 (s-1)^2} \right] = \frac{1}{2\pi i} \int_{\gamma - i \infty}^{\gamma + i \infty}{\frac{se^{st}}{(s+1)^3 (s-1)^2} \ ds}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{s}{(s+1)^3 (s-1)^2} \right] = \frac{1}{2\pi i} \oint_{C}{\frac{se^{st}}{(s+1)^3 (s-1)^2} \ ds}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{s}{(s+1)^3 (s-1)^2} \right] = \sum{\text{residuos de } \frac{se^{st}}{(s+1)^3 (s-1)^2} \text{ en los polos } s=-1 \ \text{y} \ s=1}$

El residuo en el polo triple $s=-1$ es

$\displaystyle \lim_{s \rightarrow -1}{\frac{1}{2!} \frac{d^2}{{ds}^2} \left[(s+1)^3 \cdot \frac{se^{st}}{(s+1)^3 (s-1)^2} \right]} = \frac{1}{2} \lim_{s \rightarrow -1}{\frac{d^2}{{ds}^2} \left[\frac{se^{st}}{(s-1)^2} \right]}$

$\displaystyle \lim_{s \rightarrow -1}{\frac{1}{2!} \frac{d^2}{{ds}^2} \left[(s+1)^3 \cdot \frac{se^{st}}{(s+1)^3 (s-1)^2} \right]} = \frac{1}{16} e^{-t} (1-2t^2)$

y el residuo en el polo doble $s=1$ es

$\displaystyle \lim_{s \rightarrow 1}{\frac{1}{1!} \frac{d^2}{{ds}^2} \left[(s-1)^2 \cdot \frac{se^{st}}{(s+1)^3 (s-1)^2} \right]} = \frac{1}{1} \lim_{s \rightarrow 1}{\frac{d}{ds} \left[\frac{se^{st}}{(s+1)^3} \right]}$

$\displaystyle \lim_{s \rightarrow 1}{\frac{1}{1!} \frac{d^2}{{ds}^2} \left[(s-1)^2 \cdot \frac{se^{st}}{(s+1)^3 (s-1)^2} \right]} = \frac{1}{16} e^{t} (2t-1)$

Regresando

$\displaystyle \mathcal{L}^{-1} \left[\frac{s}{(s+1)^3 (s-1)^2} \right] = \sum{\text{residuos de } \frac{se^{st}}{(s+1)^3 (s-1)^2} \text{ en los polos } s=-1 \ \text{y} \ s=1}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{s}{(s+1)^3 (s-1)^2} \right] = \frac{1}{16} e^{-t} (1-2t^2) + \frac{1}{16} e^t (2t-1)$

Finalmente

$\displaystyle \therefore \mathcal{L}^{-1} \left[\frac{s}{(s+1)^3 (s-1)^2} \right] = \frac{1}{16} e^{-t} (1-2t^2) + \frac{1}{16} e^t (2t-1)$

Problema 4. Calcular $\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s^2+1)^2} \right]$ .

Solución. Del denominador se observa que,

$\displaystyle \frac{1}{(s^2+1)^2} = \frac{1}{[(s+i)(s-i)]^2} = \frac{1}{(s+i)^2 (s-i)^2}$

Entonces,

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s^2+1)^2} \right] = \mathcal{L}^{-1} \left[\frac{1}{(s+i)^2 (s-i)^2} \right]$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s^2+1)^2} \right] = \frac{1}{2\pi i} \int_{\gamma - i \infty}^{\gamma + i \infty}{\frac{e^{st}}{(s+i)^2 (s-i)^2} \ ds}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s^2+1)^2} \right] = \frac{1}{2\pi i} \oint_{C}{\frac{e^{st}}{(s+i)^2 (s-i)^2} \ ds}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s^2+1)^2} \right] = \sum{\text{residuos de } \frac{e^{st}}{(s+i)^2 (s-i)^2} \text{ en los polos } s=-i \ \text{y} \ s=i}$

El residuo en el polo doble (o de orden 2) $s=-i$ es

$\displaystyle \lim_{s \rightarrow -i}{\frac{1}{1!} \frac{d}{ds} \left[(s+i)^2 \cdot \frac{e^{st}}{(s+i)^2 (s-i)^2} \right]} = \lim_{s \rightarrow -i}{\frac{1}{1} \frac{d}{ds} \left[\frac{e^{st}}{(s-i)^2} \right]}$

$\displaystyle \lim_{s \rightarrow -i}{\frac{1}{1!} \frac{d}{ds} \left[(s+i)^2 \cdot \frac{e^{st}}{(s+i)^2 (s-i)^2} \right]} = - \frac{1}{4} te^{it} - \frac{1}{4} ie^{it}$

Y el residuo en el polo doble (o de orden 2) $s=i$ es

$\displaystyle \lim_{s \rightarrow i}{\frac{1}{1!} \frac{d}{ds} \left[(s-i)^2 \cdot \frac{e^{st}}{(s+i)^2 (s-i)^2} \right]} = \lim_{s \rightarrow i}{\frac{1}{1} \frac{d}{ds} \left[\frac{e^{st}}{(s+i)^2} \right]}$

$\displaystyle \lim_{s \rightarrow -i}{\frac{1}{1!} \frac{d}{ds} \left[(s+i)^2 \cdot \frac{e^{st}}{(s+i)^2 (s-i)^2} \right]} = - \frac{1}{4} te^{-it} - \frac{1}{4} ie^{-it}$

Regresando

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s^2+1)^2} \right] = \sum{\text{residuos de } \frac{e^{st}}{(s+i)^2 (s-i)^2} \text{ en los polos } s=-i \ \text{y} \ s=i}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s^2+1)^2} \right] = -\frac{1}{4} te^{it} - \frac{1}{4} ie^{it} - \frac{1}{4} te^{-it} - \frac{1}{4} ie^{-it}$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s^2+1)^2} \right] = -\frac{1}{4} t(e^{it} + e^{-it}) - \frac{1}{4} i(e^{it} + e^{-it})$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s^2+1)^2} \right] = -\frac{1}{2} t(\frac{e^{it} + e^{-it}}{2}) - \frac{1}{2} i(\frac{e^{it} + e^{-it}}{2})$

$\displaystyle \mathcal{L}^{-1} \left[\frac{1}{(s^2+1)^2} \right] = -\frac{1}{2} t\cos{t} - \frac{1}{2}\sin{t}$

Finalmente,

$\displaystyle \therefore \mathcal{L}^{-1} \left[\frac{1}{(s^2+1)^2} \right] = -\frac{1}{2} t\cos{t} - \frac{1}{2}\sin{t}$

Utilización del teorema del residuo para hallar la transformada inversa de Laplace de una función. Laplace.

Introducción

Demostración

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Utilización del teorema del residuo para hallar la transformada inversa de Laplace de una función. Laplace.

Introducción

Demostración

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta