Operaciones con vectores
Sean y
vectores y sea “c” un escalar. Las operaciones con vectores son las siguientes:
1. La suma vectorial de u y v es el vector
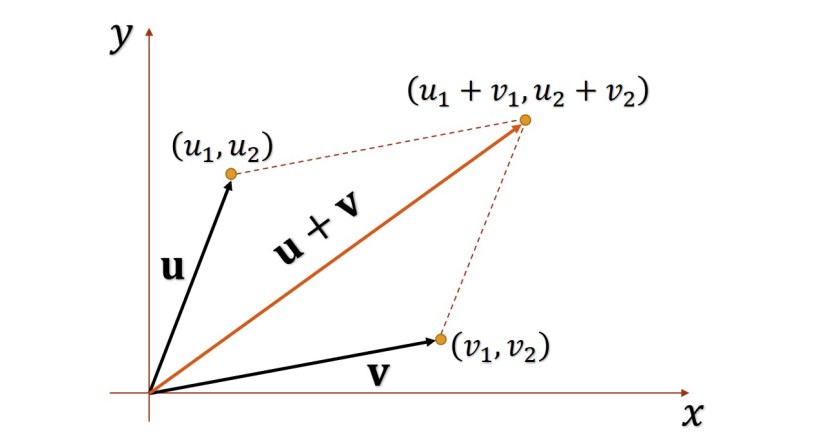
Figura 1. Suma vectorial (vista general). 
Figura 2. Suma vectorial (más detalles).
2. El múltiplo escalar de «c» y u es el vector
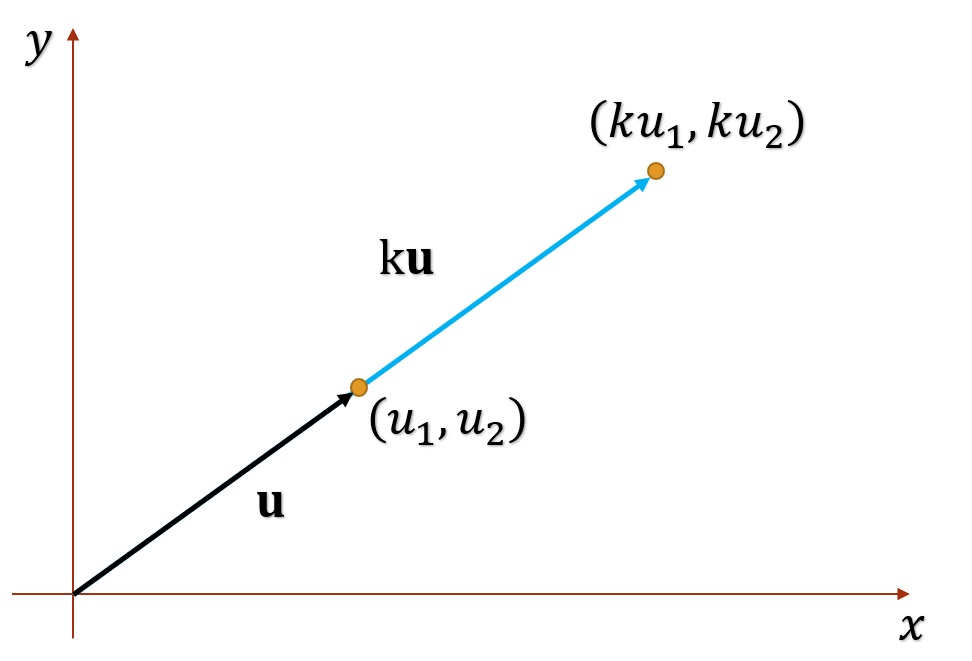
Figura 3. Multiplicación vectorial (vista general). 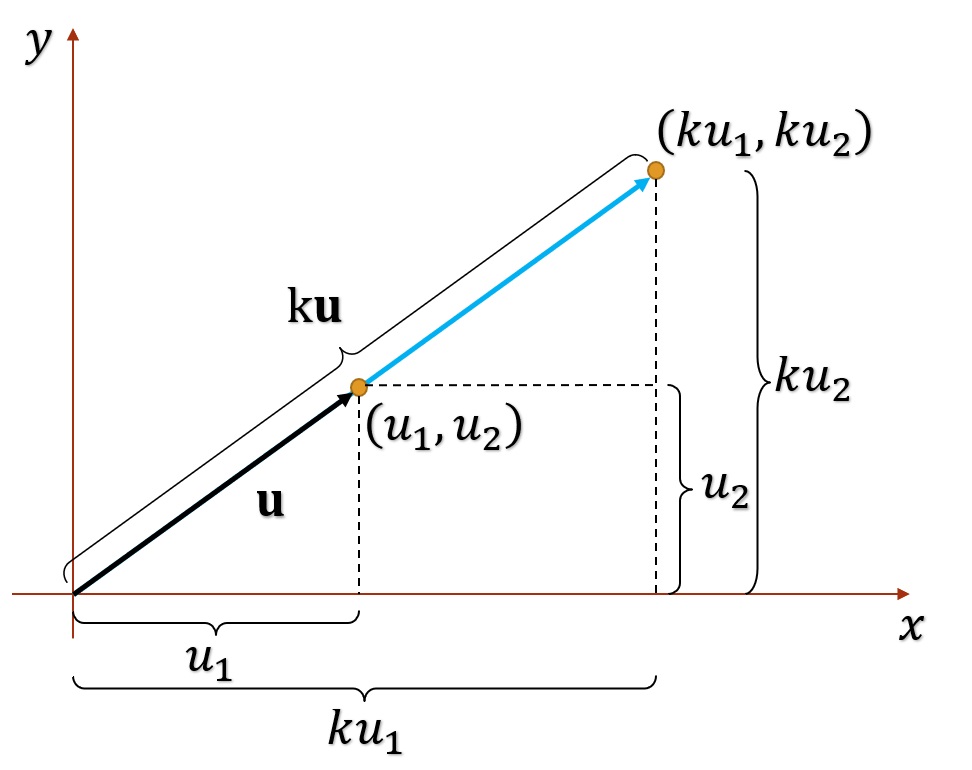
Figura 4. Multiplicación vectorial (más detalles).
3. El negativo de v es el vector
4. La diferencia de u y v es
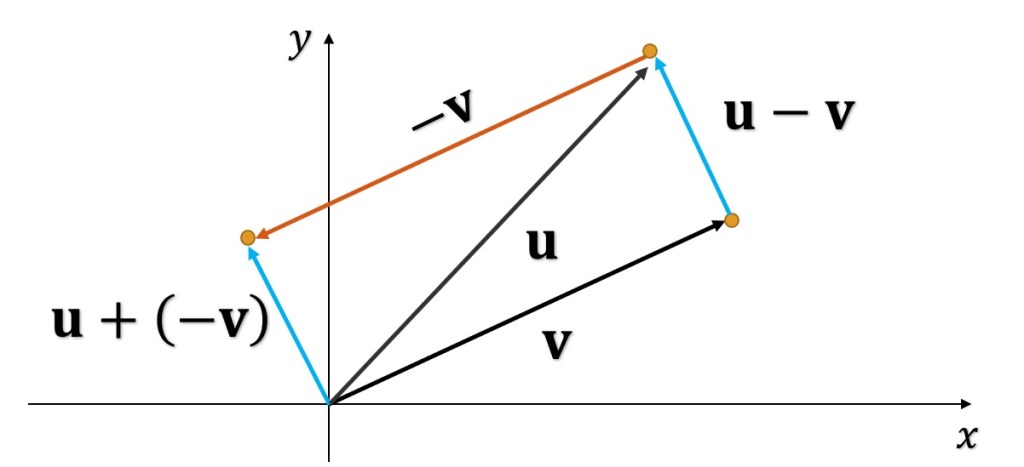
Figura 5. resta, diferencia o sustracción de vectores.
Problema resuelto
Problema. Dados v=(-2,5) y w=(3,4), encontrar cada uno de los vectores.
- a) (1/2) v
- b) w – v
- c) v + 2w
Solución. De los siguientes vectores
Solución a). Realizando la operación indicada
Solución b). Realizando la operación indicada
Solución c). Realizando la operación indicada
Propiedades de las operaciones con vectores
Sean u, v y w los vectores en el plano, y sean c y d los escalares. Las propiedades de las operaciones con vectores son las siguientes:
| 1. | Propiedad conmutativa. |
| 2. | Propiedad asociativa. |
| 3. | Propiedad de la identidad aditiva. |
| 4. | Propiedad del inverso aditivo. |
| 5. | |
| 6. | Propiedad distributiva. |
| 7. | Propiedad distributiva. |
| 8. |
Vector unitario en la dirección de v
Si v es un vector distinto de cero en el plano, entonces el vector unitario u es:
Problemas resueltos.
Problema. Hallar un vector unitario en la dirección de v = (-2,5) y verificar cual es su magnitud.
Solución. Hallando el vector unitario en base a la fórmula:
Y verificando la magnitud del vector u:
Algo importante
La longitud de la suma de dos vectores no siempre es igual a la suma de sus longitudes. Para este tipo de casos, basta con tomar los vectores u y v mostrados en la figura _. Se debe considerar u y v como dos de los lados de un triángulo, para sí poder ver que la longitud del tercer lado sea ||u + v||, y se tiene

La igualdad sólo se da si los vectores u y v tienen la misma dirección. A este resultado se le llama la desigualdad del triángulo para vectores.
lol……. :):):):):):):)
Me gustaMe gusta