Tiro horizontal. Física.

Introducción

El tiro horizontal se diferencia del tiro parabólico en que al inicio del movimiento el proyectil sólo presenta una velocidad horizontal, ( $v_x$ ), debido a que no existe ángulo de inclinación. Por tanto, no presenta velocidad vertical inicial, ( $v_{iy} = 0$ ), lo que implica que $v_x = v_{ix}$ . Su gráfica característica es la figura 1.

Figura 1. Representación gráfica del tiro horizontal.

Al analizar el tiempo de caída de dos cajas lanzadas al mismo tiempo desde un avión que vuela horizontalmente y con una velocidad constante, ambas legan al suelo al mismo tiempo, aunque la caja 1 se dejó caer libremente, mientras que la caja 2 se lanzó hacia la derecha con cierta velocidad horizontal, probándose con ello la independencia de los movimientos correspondientes.

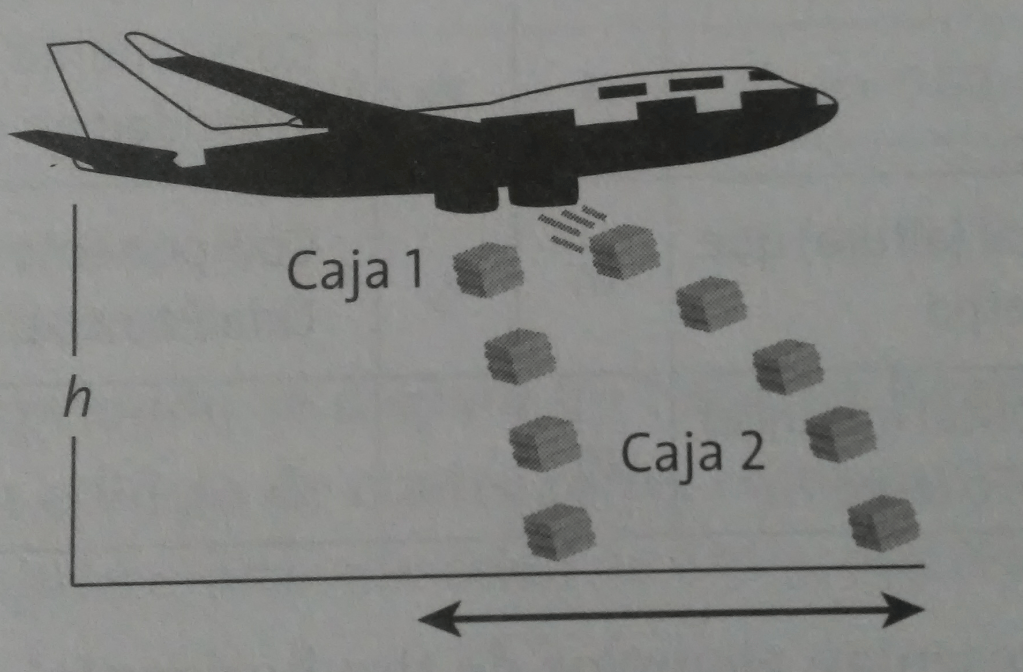
Figura 2. Análisis de dos cajas lanzadas al suelo desde un avión.

La explicación es que la caja 1 está influida exclusivamente por la fuerza de su peso y cae con una velocidad cada vez mayor debido a la aceleración de la gravedad, de modo que describe una trayectoria ligeramente parabólica. En cambio, la caja 2 en los primeros instantes describe un movimiento de tiro horizontal y posteriormente parabólico. Su velocidad se descompone en dos: la vertical debida a su peso y la horizontal, cuyo valor es la del avión que se mantiene constante y sólo le sirve para avanzar.

Las ecuaciones del tiro horizontal se obtienen a partir de las de tiro parabólico y caída libre, además se considera que la dirección positiva es hacia abajo y se sustituye altura $h$ por $y$ ; esto se muestra a continuación.

La ecuación de posición vertical $y$ se obtiene de

$\displaystyle h = v_{iy} t + \frac{gt^2}{2}$

que se reduce a

$\displaystyle y = \frac{gt^2}{2}$

ya que $v_{iy} = 0$ . La ecuación de posición horizontal $x$ , donde el movimiento es rectilíneo uniforme y la velocidad permanece constante, lo representa $x=v_{ix} t$ , que cumple en todo momento que $v_x = x_{ix}$ . La ecuación de la componente vertical de la velocidad, $v_{iy}$ , se obtiene de $v_y = v_{iy} + gt$ , que se reduce a $v_y = gt$ , debido a que $v_{iy}=0$ . Las ecuaciones para el tiro horizontal se agrupan en la siguiente tabla.

Problemas resueltos

Problema 1. Un lanzador de béisbol arroja una pelota horizontalmente desde lo alto de un barranco a una velocidad de 9 (m/s). Calcular la distancia horizontal y vertical a los 1.5 (s) de caída.

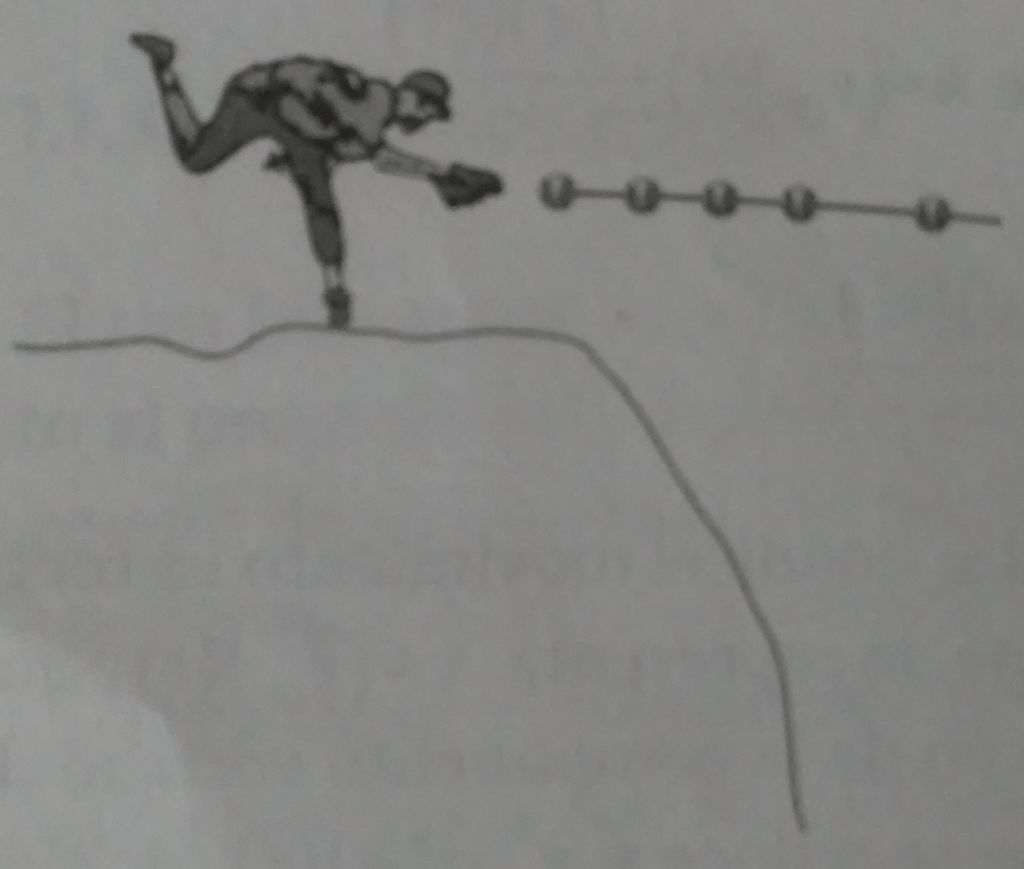
Figura 3. Un lanzador de béisbol arrojando la pelota.

Solución. Los datos que brinda el problema son $v_i = 9 \ (m/s)$ , $t=1.5 \ (s)$ y $g =9.81 \ (m/s^2)$ . Después, se sabe que

$\displaystyle v_{ix} = v_{x} = 9 \ (m/s)$

Esta igualdad es posible debido a que en la dirección horizontal se presenta el movimiento rectilíneo uniformemente y, por tanto, la velocidad es constante. El avance del proyectil logrado en forma horizontal cuando han transcurrido 1.5 (s) es

$x = v_{ix} t$

$x = (9 \ m/s)(1.5 \ s)$

$\therefore x = 13.5 \ (m)$

Y la distancia horizontal que el proyectil ha descendido cuando han transcurrido 1.5 (s) es

$\displaystyle y = \frac{gt^2}{2}$

$\displaystyle y = \frac{(9.81 \ m/s^2)(1.5 \ s)^2}{2}$

$\displaystyle \therefore y = 11.02 \ (m)$

Tanto $x$ como $y$ representan las coordenadas de la posición que tiene la pelota en este instante.

Problema 2. Con un resorte comprimido se dispara un balín en forma horizontal desde la parte superior de un edificio de cuatro pisos, equivalentes a 10 (m) de altura. Si inicialmente se le imprime una velocidad de 3 (m/s), calcular:

a) Tiempo de caída.
b) Distancia a la que cae de la base del edificio.
c) Valor de las componentes horizontal y vertical de la velocidad un momento antes de llegar al suelo.

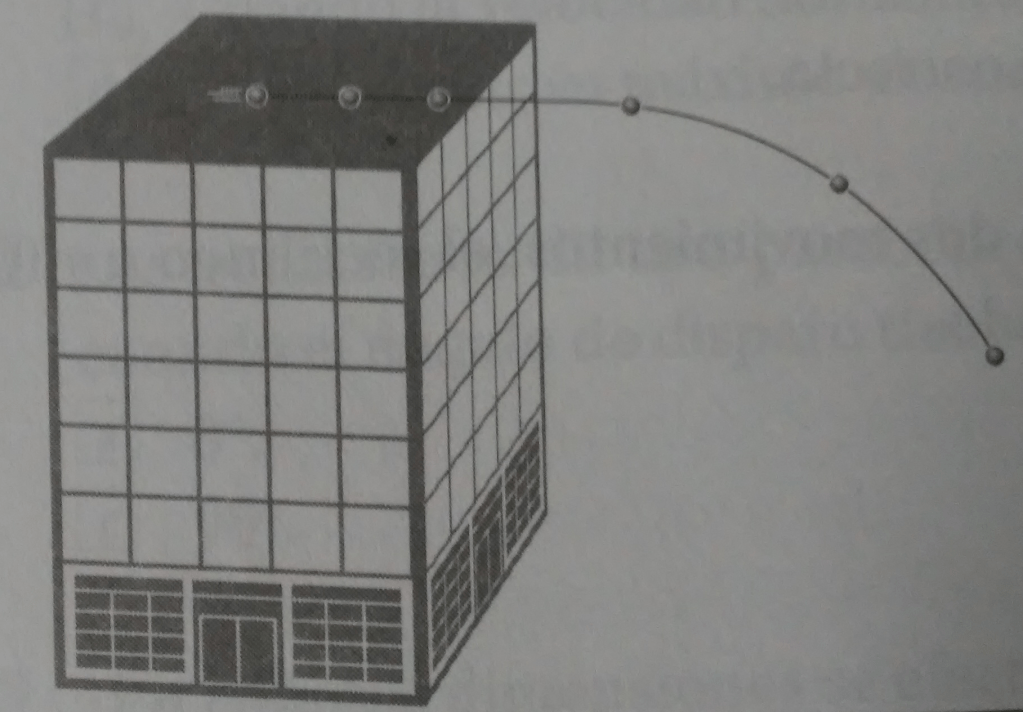
Figura 4. Un resorte comprimido disparando un balín desde un edificio.

Solución a). Primero se tiene la ecuación de la posición $y$

$\displaystyle y = \frac{gt^2}{2}$

Despejando $t$ , resulta que

$\displaystyle t = \sqrt{\frac{2y}{g}}$

Sustituyendo

$\displaystyle t = \sqrt{\frac{2(10 \ m)}{9.81 \ m/s^2}}$

$\displaystyle t = 1.43 \ s$

Solución b). Calculando la distancia

$\displaystyle x = v_{ix} \cdot t$

$\displaystyle x = (3 \ m/s)(1.43 \ s)$

$\displaystyle \therefore x = 4.29 \ m$

Solución c). El valor de la componente $x$ es

$\displaystyle v_x = v_{ix}$

$\displaystyle \therefore v_x = 3 \ m/s$

y el valor de la componente $y$ es

$\displaystyle v_y = gt$

$\displaystyle v_y = (9.81 \ m/s)(1.4 \ s)$

$\displaystyle \therefore v_y = 13.734 \ m$

Se concluye que el tiempo en que el proyectil invierte para descender 10 (m) y estrellarse al suelo es de 1.4 (s), la distancia que el proyectil avanzó horizontalmente desde que inició su movimiento es de 13734 (m) y los valores de las componentes rectangulares de la velocidad un momento antes de estrellarse al suelo son 3 (m/s) en el eje x y 13.734 (m/s) en el eje y.

Tiro horizontal. Física.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Tiro horizontal. Física.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta