Introducción
El movimiento circular se efectúa en dos dimensiones, ya que para describirlos es suficiente con manejar las coordenadas y
, aunque generalmente se expresan en función de las coordenadas polares (
y
).
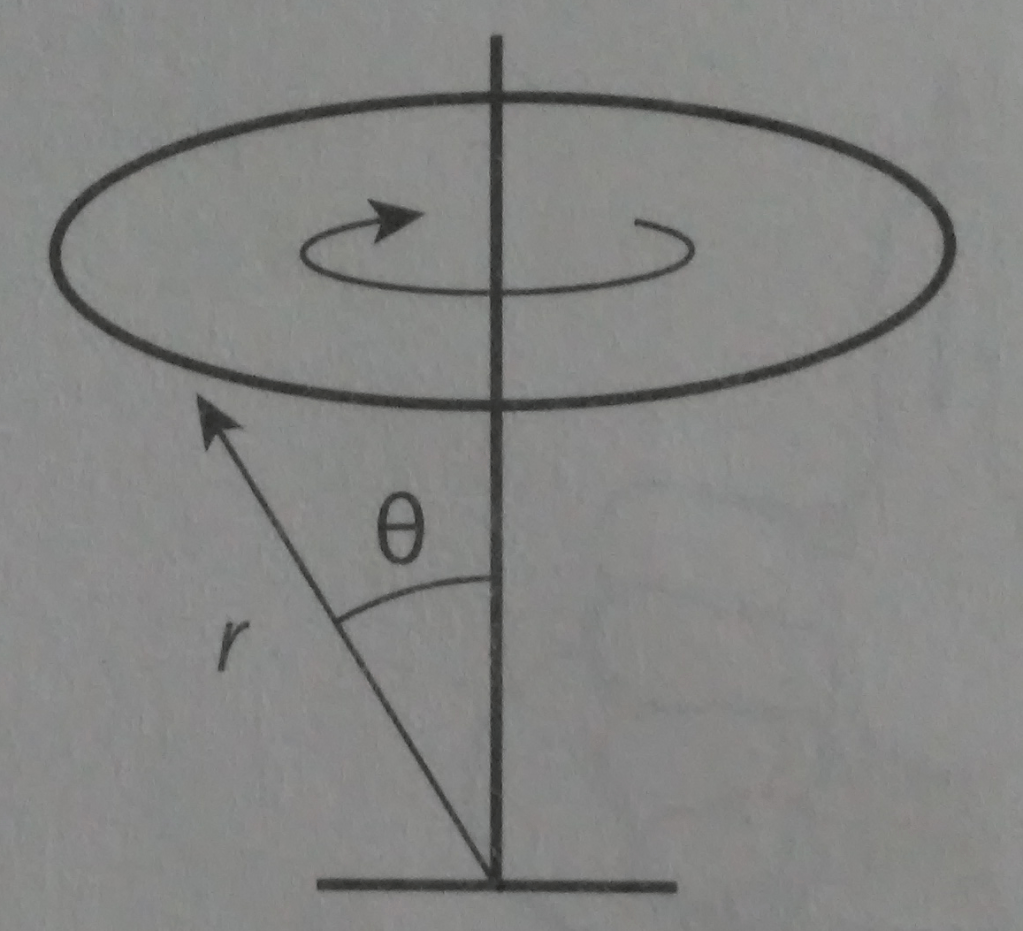
El movimiento circular se produce cuando una fuerza externa (fuera del cuerpo), llamada centrípeta, actúa en forma perpendicular a la trayectoria que describe el movimiento. El eje de rotación se considera origen del sistema de referencia y siempre varía el sentido y la dirección del vector de posición descrito, que tiene un valor igual al radio de la circunferencia, aunque su magnitud permanece constante.
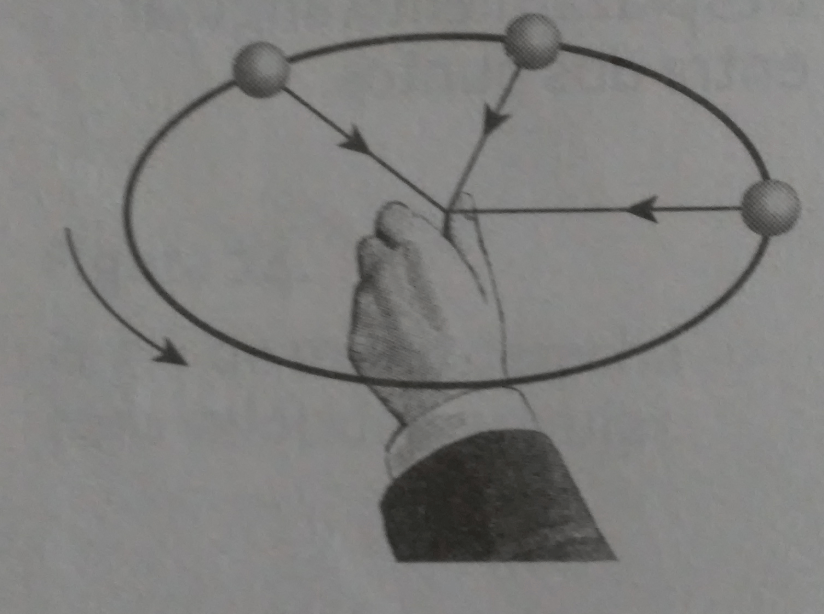
Figura 2. Cuerpo con movimiento circular. 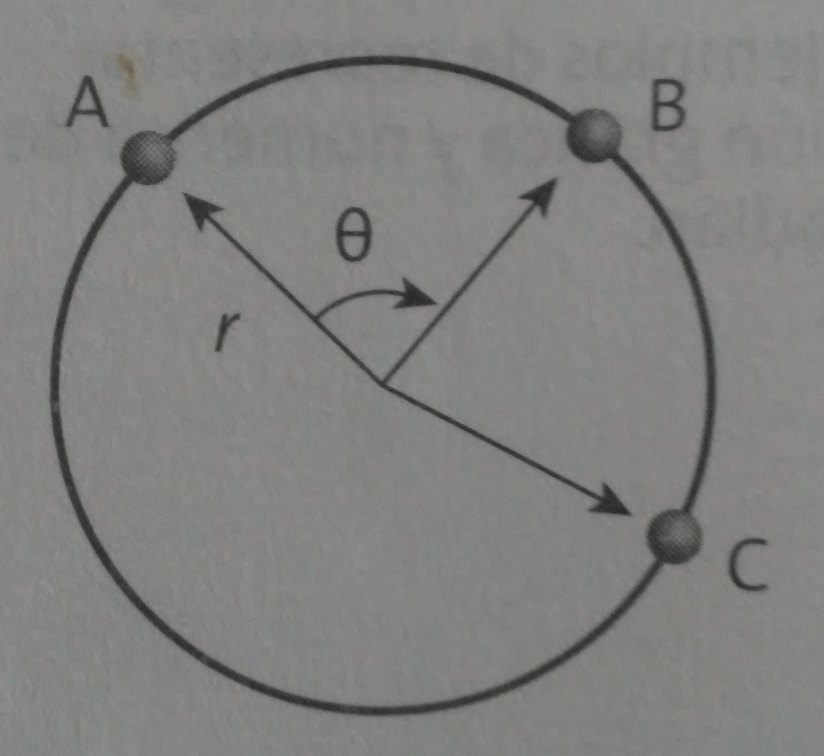
Figura 3. Vector posición.
Periodo y frecuencia
El periodo () es el tiempo que tarda un cuerpo en dar una vuelta completa. Sus unidades son los
o simplemente segundos (s). Por ejemplo, el periodo de rotación y traslación de la tierra es de 24 horas y 365 días, respectivamente.
La frecuencia () se define como el número de vueltas completas que efectúa un cuerpo en una unidad de tiempo. Sus unidades son los hertz (Hz). Cuando un cuerpo presenta una frecuencia de 1 (Hz), significa que realiza una vuelta completa (1 ciclo = 2π rad) en un segundo.
Si se observan las unidades de periodo y frecuencia, y
, son inversas, así que su producto es igual a la unidad.
Desplazamiento angular y radián
El desplazamiento angular de un cuerpo describe la cantidad de rotación. Se representa por el ángulo formado al girar el cuerpo del punto A al punto B.

Por su parte, el radián (rad) es una magnitud geométrica, un número sin unidades, es el cociente entre dos longitudes, el arco () y el radio (
).

La relación entre radianes y grados se obtiene considerando que una vuelta completa es igual a 360° y que el perímetro del círculo es , así que,
donde
o
Notas:
- El radián no es una unidad física y, por tanto, no se incluye en el análisis dimensional.
- El radián sólo se anexa al valor de la velocidad y aceleración angular.
- El radián no se incluye al trabajar con otras unidades.