Velocidad tangencial y aceleración tangencial. Física.

Velocidad tangencial

La velocidad tangencial $v_t$ , o lineal es la misma que se trató en los movimientos rectilíneos uniforme y variado, pero con la particularidad de que en el movimiento circular se presenta en el extremo de la trayectoria que describe. Su característica es que es un vector siempre perpendicular al vector posición radio.

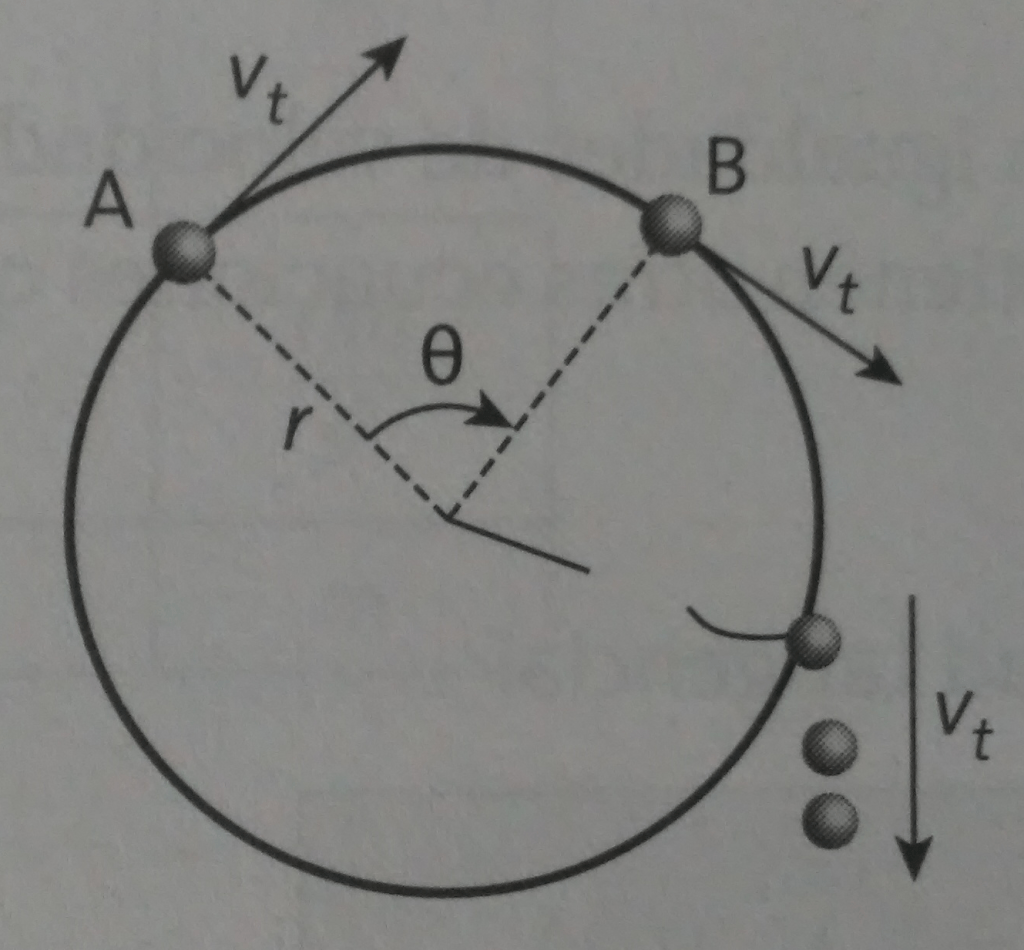
Si se trata de un movimiento circular uniforme, el valor de la velocidad tangencial no cambia; cuando cambia, el movimiento será circular variado. Pero independientemente del movimiento circular del que se trate, lo que siempre cambia es su sentido y dirección. Por ejemplo, en los juegos pirotécnicos, por la velocidad tangencial los propulsores colocados en periferia de las circunferencias hacen girar los artificios al tiempo que se queman. Cuanto más alejado del centro de rotación se encuentre el cuerpo, se moverá con mayor velocidad tangencial, ya que debe recorrer una distancia mayor. Por eso, en el juego de las coleadas la persona del exterior debe correr más rápidamente para no caerse y también por eso el carril interno en una competencia de velocidad es el que ofrece mayores ventajas.

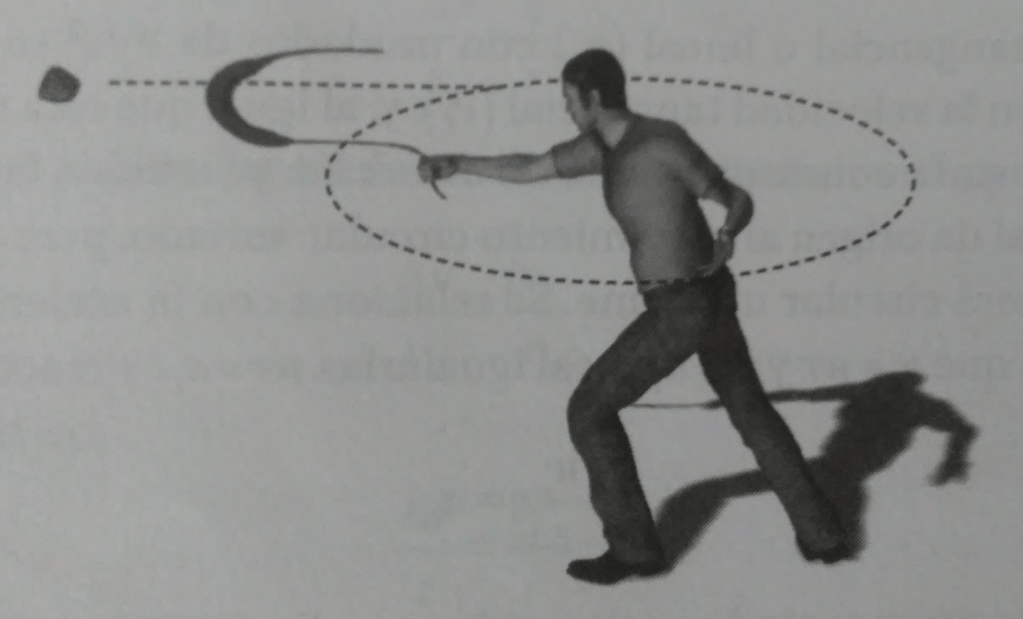
El valor de la velocidad tangencial da una idea de la rapidez con la que gira un cuerpo y la velocidad que llevaría si se saliera disparado en línea recta. Esto se aprovecha cuando se utiliza una onda para lanzar un objeto.

La relación entre la velocidad angular y la velocidad tangencial se obtiene de las dos ecuaciones siguiente

inda la idea de la rapidez con la que gira un cuerpo y la velocidad que llevaría si saliera disparado en línea recta.

$\displaystyle \theta = \frac{s}{r}$ y $\displaystyle v_t = \frac{s}{t}$

Al despejar la longitud de arco $s$ ,

$\displaystyle s= r \ \theta$ y $\displaystyle s= t \ v_t$

E igualándolas

$r \ \theta = t \ v_t$

Al reagrupar de la siguiente forma

$\displaystyle \frac{\theta}{t} = \frac{v_t}{r}$

se identifica que el lado izquierdo corresponde a la velocidad angular ( $\omega$ ); por tanto,

$\displaystyle \omega = \frac{v_t}{r}$

y al despejar $v_t$

$v_t = \theta \ r$

Junto con igualdades de la velocidad angular anteriores que abarcan el periodo y frecuencia, se obtienen otras ecuaciones que muestran a continuación

Aceleración tangencial

La aceleración tangencial o lineal ( $a_t$ ) con unidades de $m/s^2$ se presenta cuando hay un cambio en la velocidad tangencial ( $v_t$ ), y, al igual que esta última en el movimiento circular, varía constantemente de dirección y sentido.

La aceleración tangencial da origen al movimiento circular variado, pero si su valor es cero,el movimiento será circular uniforme. Se relaciona con la aceleración angular ( $\alpha$ ), si se considera que