Superficies cuadráticas. Cálculo vectorial.

La ecuación de una superficie cuadrática en el espacio es una ecuación de segundo grado de la forma

$\displaystyle Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Iz+J=0$

Hay seis tipos básicos de superficies cuadráticas como son la elipsoide, hiperboloide de una hoja, hiperboloide de dos hojas, cono elíptico, paraboloide elíptico y paraboloide hiperbólico.

A la intersección de una superficie con un plano se le denomina traza de la superficie en el plano. Para visualizar una superficie en el espacio, es útil determinar sus trazas en algunos planos estratégicos. Las trazas de las superficies cuadráticas son cónicas. Estas trazas, junto con la forma canónica o estándar de la ecuación de cada superficie cuadrática, se visualiza en las siguientes figuras.

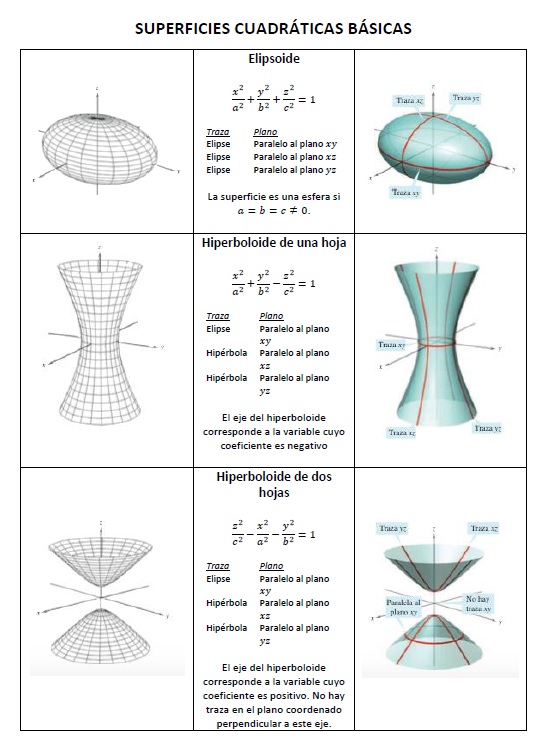
*Figura 1. Superficies cuadráticas básicas. (parte 1)*

Figura 2. Superficies cuadráticas básicas (parte 2).

Para clasificar una superficie cuadrática, se debe comenzar por escribir la superficie en la forma canónica o estándar. Después, se determinan varias trazas en los planos coordenados o en planos paralelos a los planos coordenados.

Problemas resueltos

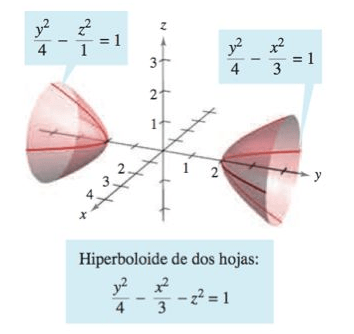
Problema 1. Clasificar y dibujar la superficie dada por $4x^2-3y^2+12z^2+12=0$ .

Solución. Primero, se escribe la ecuación en forma canónica (o estándar).

$\displaystyle 4x^2-3y^2+12z^2+12=0$

$\displaystyle \frac{1}{12} (4x^2-3y^2+12z^2+12) = \frac{1}{12} (0)$

$\displaystyle \frac{4}{12} x^2 - \frac{3}{12} y^2 + \frac{12}{12} z^2 + \frac{12}{12} = 0$

$\displaystyle \frac{1}{3} x^2 - \frac{1}{4} y^2 + (1) z^2 + 1 = 0$

$\displaystyle \frac{x^2}{3} - \frac{y^2}{4} + z^2 + 1 = 0$

$\displaystyle \frac{x^2}{3} - \frac{y^2}{4} + z^2 = - 1$

$\displaystyle - \frac{x^2}{3} + \frac{y^2}{4} - z^2 = 1$

$\displaystyle \frac{y^2}{4} - \frac{x^2}{3} - z^2 = 1$

Para graficar esta superficie, se hallan las trazas en los planos coordenados.

Finalmente, se tiene la superficie de un hiperboloide de dos hojas con el eje $y$ como su eje. Su gráfica es la siguiente

Problema 2. Clasifique y dibuje la superficie dada por $x-y^2-4z^2=0$ .

Solución. Como $x$ está elevada sólo a la primera potencia, la superficie es un paraboloide. El eje del paraboloide es el eje $x$ . En la forma canónica o estándar, la ecuación es

$\displaystyle x-y^2-4z^2=0 \rightarrow x = y^2+4z^2$

Después, realizando las trazas

Se concluye que la superficie es un paraboloide elíptico. Su gráfica es la siguiente

Problema 3. Clasificar y dibujar la superficie dada por

$\displaystyle x^2+2y^2+z^2-4x+4y-2z+3=0$

Solución. Al completar el cuadrado de cada variable se obtiene

$\displaystyle x^2+2y^2+z^2-4x+4y-2z+3=0$

$\displaystyle (x^2-4x)+(2y^2+4y)+(z^2-2z)+3=$

$\displaystyle (x^2-4x)+2(y^2+2y)+(z^2-2z)=-3$

$\displaystyle (x^2-4x+4-4)+2(y^2+2y+1-1)+(z^2-2z+1-1)=-3$

$\displaystyle (x^2-4x+4)-4)+2(y^2+2y+1)+(z^2-2z+1)=-3+4+2+1$

$\displaystyle (x-4)^2+2(y+1)^2+(z-1)^2=4$

$\displaystyle \frac{1}{4} [(x-4)^2+2(y+1)^2+(z-1)^2]=\frac{1}{4} (4)$

$\displaystyle \frac{(x-4)^2}{4} + \frac{(y+1)^2}{2} + \frac{(z-1)^2}{4}= 1$

Realizando los trazos

Se concluye que esta ecuación representa la superficie de un elipsoide con centro en el punto $(2,-1,1)$ . Su gráfica se muestra en la figura 5.

Figura 5. Elipsoide con centro en $(2,-1,1)$ .

Figura 5. Elipsoide con centro en $(2,-1,1)$ .

Traza $xy$ ( $z=0$ )	$\displaystyle \frac{y^2}{4} - \frac{x^2}{3} = 1$	Es una hipérbola
Traza $xz$ ( $y=0$ )	$\displaystyle \frac{x^2}{3} + z^2 = - 1$	No hay traza
Traza $yz$ ( $x=0$ )	$\displaystyle \frac{y^2}{4} - z^2 = 1$	Es una hipérbola

Traza $xy$ ( $z=0$ )	$\displaystyle x=y^2$	Es una parábola
Traza $xz$ ( $y=0$ )	$\displaystyle x=4z^2$	Es una parábola
Paralelo al plano $yz$ ( $x=4$ )	$\displaystyle \frac{y^2}{4} + z^2 = 1$	Es una elipse

Traza $xy$ ( $z=1$ )	$\displaystyle \frac{(x-4)^2}{4} + \frac{(y+1)^2}{2} = 1$	Es una elipse
Traza $xz$ ( $y=-1$ )	$\displaystyle \frac{(x-4)^2}{4} + \frac{(z-1)^2}{4}=1$	Es una elipse
Traza $yz$ ( $x=4$ )	$\displaystyle \frac{(y+1)^2}{2} + \frac{(z-1)^2}{4} = 1$	Es una elipse

Superficies cuadráticas. Cálculo vectorial.

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Superficies cuadráticas. Cálculo vectorial.

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta